Изгибаемый многогранник | это... Что такое Изгибаемый многогранник? (original) (raw)

Многогра́нник (точнее — многогранная поверхность) называется изгиба́емым, если его пространственную форму можно изменить такой непрерывной во времени деформацией, при которой каждая грань не изменяет своих размеров (то есть движется как твёрдое тело), а деформация осуществляется только за счёт непрерывного изменения двугранных углов. Такая деформация называется непрерывным изгибанием многогранника.

Свойства и примеры

В теории изгибаемых многогранников известно немало красивых и нетривиальных утверждений. Ниже приведены наиболее важные из установленных на сегодня фактов, придерживаясь хронологического порядка:

Никакой выпуклый многогранник не может быть изгибаемым. Это немедленно вытекает из теоремы Коши об однозначной определённости выпуклого многогранника, доказанной в 1813 году.
Первые примеры изгибаемых многогранников были построены бельгийским инженером и математиком Раулем Брикаром в 1897 году [1]. Сейчас их называют октаэдрами Брикара. Они не только невыпуклые, но и имеют самопересечения, что не позволяет построить их движущуюся картонную модель.
В 1976 году американский математик Роберт Коннелли впервые построил изгибаемый многогранник без самопересечений[2].
Из всех известных на сегодняшний день изгибаемых многогранников без самопересечений наименьшее число вершин (девять) имеет многогранник, построенный немецким математиком Клаусом Штеффеном (нем. Klaus Steffen)[3].
Известны примеры изгибаемых многогранников, являющихся реализациями тора [4] или бутылки Клейна или вообще двумерной поверхности любого топологического рода.
Из формулы Шлефли следует, что любой изгибаемый многогранник в процессе изгибания сохраняет так называемую интегральную среднюю кривизну, то есть число, равное $\sum |\ell|(\pi-\alpha(\ell))$ , где $|\ell|$ — длина ребра $~\ell$ , $~\alpha(\ell)$ — величина внутреннего двугранного угла при ребре $~\ell$ , а сумма распространяется на все рёбра многогранника. См. также [5].
Теорема Сабитова[6]: Любой изгибаемый многогранник в процессе изгибания сохраняет свой объём, то есть он будет изгибаться даже если его заполнить несжимаемой жидкостью.

Изгибаемый октаэдр Брикара первого типа
Изгибаемый октаэдр Брикара второго типа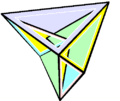
Изгибаемый многогранник Штеффена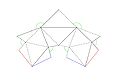
Развёртка изгибаемого многогранника Штеффена

Гипотезы

Несмотря на значительный прогресс, в теории изгибаемых многогранников остаётся много нерешённых проблем. Вот несколько открытых гипотез:

многогранник Штеффена имеет наименьшее число вершин среди всех изгибаемых многогранников, не имеющих самопересечений[7];
если один многогранник, не имеющий самопересечений, получен из другого многогранника, который также не имеет самопересечений, непрерывным изгибанием, то эти многогранники равносоставлены, то есть первый можно разбить на конечное число тетраэдров, каждый из этих тетраэдров независимо от других можно передвинуть в пространстве и получить разбиение второго многогранника[8].

Обобщения

Всё сказанное выше относилось к многогранникам в трёхмерном евклидовом пространстве. Однако данное выше определение изгибаемого многогранника примени́мо и к многомерным пространствам и к неевклидовым пространствам, таким как сферическое пространство и пространство Лобачевского. Для них также известны как нетривиальные теоремы, так и открытые вопросы. Например:

доказано, что в четырёхмерном евклидовом пространстве, пространстве Лобачевского размерности 3 и 4, а также в сферическом пространстве размерности 3 и 4 имеются изгибаемые многогранники[9], в то время как существование изгибаемых многогранников в евклидовых пространствах размерности 5 и выше остаётся открытым вопросом;
доказано, что любой изгибаемый многогранник в евклидовом пространстве размерности 3 и выше сохраняет свою интегральную среднюю кривизну в процессе изгибания[5], но неизвестно всякий ли изгибаемый многогранник в евклидовом пространстве размерности 4 и выше сохраняет свой объём в процессе изгибания;
доказано, что в трёхмерном сферическом пространстве существует изгибаемый многогранник, объём которого непостоянен в процессе изгибания[10], но не известно обязательно ли сохраняется объём изгибаемого многогранника в трёхмерном пространстве Лобачевского.

Сделай сам

Сделать модель изгибаемого многогранника Штеффена совсем не трудно. Опишем это процесс шаг за шагом.

Сохраните файл с развёрткой многогранника Штеффена из приведённой выше «галереи изображений».
Увеличьте развёртку в 2—3 раза и распечатайте его на принтере (при этом желательно использовать плотную бумагу или полукартон).
Вырежьте развёртку по контуру, состоящему из красных, синих и чёрных (сплошных и пунктирных) отрезков.
Несколько раз перегните бумагу по оставшимся на развёртке сплошным и пунктирным отрезкам. Выполняя последующие действия следует придавать поверхности такую форму, чтобы сплошные отрезки были «горными хребтами» (то есть выступали из многогранника наружу), а пунктирные отрезки были «долинами» (то есть вдавались бы внутрь многогранника).
Изогните поверхность в пространстве и склейте между собой каждые два чёрных отрезка, соединённых на развёртке зелёной дугой окружности.
Склейте между собой два синих отрезка.
Склейте между собой два красных отрезка.

Модель многогранника Штеффена готова.

Научная литература

В. А. Александров, Новый пример изгибаемого многогранника, Сиб. мат. журн. 1995. Т. 36, No 6. С. 1215—1224.
Н. Х. Кёйпер (англ.), Изгибаемые полиэдральные сферы в , по Роберту Коннелли, в кн. под ред. А. Н. Колмогорова и С. П. Новикова: Исследования по метрической теории поверхностей. М.: Мир. 1980. С. 210—227.
P. Коннелли, Об одном подходе к проблеме неизгибаемости. Там же. С. 164—209.
Р. Коннелли, Некоторые предположения и нерешённые вопросы в теории изгибаний. Там же. С. 228—238.
И. Г. Максимов, Неизгибаемые многогранники с малым количеством вершин, Фундам. прикл. матем. 2006. Т. 12, No. 1. С. 143—165.
С. Н. Михалёв, Некоторые необходимые метрические условия изгибаемости подвесок, Вестник МГУ, Сер. I, 2001, No. 3, 15—21.
И. Х. Сабитов, Объём многогранника как функция его метрики, Фундам. прикл. матем. 1996. Т. 2, No. 4. С. 1235—1246.
И. Х. Сабитов, Обобщённая формула Герона — Тарталья и некоторые её следствия, Матем. сб. 1998. Т. 189, No. 10. С. 105—134.

Примечания

↑ R. Bricard. Mémoire sur la théorie de l’octaèdre articulé. J. Math. Pures Appl. 1897. 3. P. 113—150 (см. также английский перевод).
↑ R. Connelly, The rigidity of polyhedral surfaces, Math. Mag. 52 (1979), no. 5, 275—283.
↑ М. Берже, Геометрия. М.: Мир, 1984. Т. 1. С. 516—517.
↑ В. А. Александров, Новый пример изгибаемого многогранника, Сиб. мат. журн. 1995. Т. 36, No 6. С. 1215—1224.
↑ 1 2 R. Alexander, Lipschitzian mappings and total mean curvature of polyhedral surfaces. I, Trans. Amer. Math. Soc. 1985. Vol. 288, no. 2, 661—678.
↑ И. Х. Сабитов, Объем многогранника как функция длин его ребер, Фундам. прикл. матем. 1996. Т. 2, № 1. С. 305—307.
↑ И. Г. Максимов, Неизгибаемые многогранники с малым количеством вершин, Фундам. прикл. матем. 2006. Т. 12, No. 1. С. 143—165.
↑ См. стр. 231 книги под ред. А. Н. Колмогорова и С. П. Новикова: Исследования по метрической теории поверхностей. М.: Мир. 1980. На английском эта гипотеза была впервые опубликована в статье R. Connelly, The rigidity of polyhedral surfaces, Math. Mag. 1979. Vol. 52. P. 275—283.
↑ H. Stachel, Flexible octahedra in the hyperbolic space, в книге под ред. A. Prékopa: Non-Euclidean geometries. János Bolyai memorial volume. Papers from the international conference on hyperbolic geometry, Budapest, Hungary, July 6—12, 2002. New York, NY: Springer. Mathematics and its Applications 581, 209—225 (2006).
↑ V. Alexandrov, An example of a flexible polyhedron with nonconstant volume in the spherical space, Beitr. Algebra Geom. 38, No.1, 11—18 (1997). ISSN 0138-4821.

Многогранники
Правильные (Платоновы тела)	Трёхмерные Правильный тетраэдр • Куб • Октаэдр • Додекаэдр • Икосаэдр Четырёхмерные 6 правильных многогранников Большей размерности N-мерный куб • N-мерный октаэдр • N-мерный тетраэдр
Звёздчатый додекаэдр • Звёздчатый икосододекаэдр • Звёздчатый икосаэдр • Звёздчатый многогранник • Звёздчатый октаэдр
Выпуклые	Архимедовы тела Кубооктаэдр • Икосододекаэдр • Усечённый тетраэдр • Усечённый октаэдр • Усечённый икосаэдр • Усечённый куб • Усечённый додекаэдр • Ромбокубоктаэдр • Ромбоикосододекаэдр • Ромбоусечённый кубоктаэдр • Ромбоусечённый икосододекаэдр • Курносый куб • Курносый додекаэдр • Усечённый кубооктаэдр • Усечённый икосододекаэдр • Правильная призма • Антипризма Каталановы тела Ромбододекаэдр • Ромботриаконтаэдр • Триакистетраэдр • Тетракисгексаэдр • Пентакисдодекаэдр • Триакисоктаэдр • Триакисикосаэдр • Дельтоидальный икоситетраэдр • Дельтоидальный гексеконтаэдр •Пентагональный икоситетраэдр • Пентагональный гексеконтаэдр • Дисдакисдодекаэдр • Дисдакистриаконтаэдр Без полной пространственной симметрии Пирамида • Призма • Бипирамида • Антипризма • Зоноэдр • Параллелепипед • Ромбоэдр •Призматоид• Усечённая пирамида• Пентагондодекаэдр • Параллелоэдр
Формулы, теоремы, теории	Теорема Александрова о выпуклых многогранниках • Теорема Бликера • Теорема Коши о многогранниках • Теорема Линделёфа о многограннике • Теорема Минковского о многогранниках • Теорема Сабитова • Теорема Эйлера для многогранников • Теория перекатывания многогранников • Формула Шлефли
Прочее	Ортоцентрический тетраэдр • Равногранный тетраэдр • Прямоугольный параллелепипед • Группа многогранника • Двенадцатигранники • Телесный угол • Единичный куб • Изгибаемый многогранник • Развёртка • Символ Шлефли • Многомерные (N-мерный тетраэдр • Тессеракт • Пентеракт • Хексеракт • Хептеракт • Октеракт • Энтенеракт • Декеракт • Гиперкуб)