Ротор (математика) | это... Что такое Ротор (математика)? (original) (raw)

У этого термина существуют и другие значения, см. Ротор.

Ро́тор, или вихрь — векторный дифференциальный оператор над векторным полем.

Обозначается

$\operatorname{rot}$ (в русскоязычной[1] литературе) или

$\operatorname{curl}$ (в англоязычной литературе),

а также - как векторное умножение дифференциального оператора набла на векторное поле:

$\mathbf{\nabla} \times.$

Результат действия этого оператора на конкретное векторное поле F называется ротором поля F или, короче, просто ротором F и представляет собой новое векторное[2] поле:

$\operatorname{rot}\,\mathbf F\equiv\mathbf{\nabla} \times \mathbf{F}.$

Поле rot F (длина и направление вектора rot F в каждой точке пространства) характеризует в некотором смысле[3] вращательную составляющую поля F соответственно в каждой точке.

Содержание

1 Интуитивный образ
2 Математическое определение
- 2.1 Связанные определения
- 2.2 Обобщение
3 Физическая интерпретация
4 Основные свойства
- 4.1 Свойства, непосредственно получаемые из обычных правил дифференцирования
- 4.2 Теорема Стокса
5 Альтернативные определения
6 Ротор в криволинейных координатах
- 6.1 Общий случай
- 6.2 В ортогональных криволинейных координатах
7 Примеры
8 Примечания
9 См. также

Интуитивный образ

Если v(x,y,z) - поле скорости движения газа (или течения жидкости), то rot v - вектор, пропорциональный вектору угловой скорости очень маленькой и лёгкой пылинки (или шарика), находящегося в потоке (и увлекаемого движением газа или жидкости; хотя центр шарика можно при желании закрепить, лишь бы он мог вокруг него свободно вращаться).

Конкретно rot v = 2 ω, где ω - эта угловая скорость.

Простую иллюстрацию этого факта - см. ниже.

Эта аналогия может быть сформулирована вполне строго (см. ниже). Основное определение через циркуляцию (данное в следующем параграфе) можно считать эквивалентным полученному таким образом.

Математическое определение

Ротор $\operatorname{rot}\, \mathbf a$ векторного поля $\mathbf a$ — есть вектор, проекция которого $\operatorname{rot} _ \mathbf n \mathbf a$ на каждое направление n есть предел отношения циркуляции векторного поля по контуру L, являющемуся краем плоской площадки Δ_S_, перпендикулярной этому направлению, к величине этой площадки, когда размеры площадки стремятся к нулю, а сама площадка стягивается в точку:

$\operatorname{rot} _ \mathbf n \mathbf a=\lim_{\Delta S\to 0}\frac{\oint\limits_{L}\mathbf{ a\cdot \, dr}}{\Delta S}$ .

Направление обхода контура выбирается так, чтобы, если смотреть в направлении $\mathbf n$ , контур L обходился по часовой стрелке[4].

В трёхмерной декартовой системе координат ротор (в соответствии с определением выше) вычисляется следующим образом (здесь F - обозначено некое векторное поле с декартовыми компонентами F_x, F_y, F_z , а $\mathbf e_x, \mathbf e_y, \mathbf e_z$ - орты декартовых координат):

$\operatorname{rot}\;(F_x \mathbf e_x + F_y\, \mathbf e_y + F_z \mathbf e_z) =$

$= \left( \partial_y F_z - \partial_z F_y \right) \mathbf e_x+ \left( \partial_z F_x - \partial_x F_z \right) \mathbf e_y+ \left( \partial_x F_y - \partial_y F_x \right) \mathbf e_z \equiv$

$\equiv \left(\frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}\right) \mathbf e_x+ \left(\frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}\right) \mathbf e_y+ \left(\frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}\right) \mathbf e_z.$

или

$(\operatorname{rot}\;\mathbf F)_x = \partial_y F_z - \partial_z F_y \equiv \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z}$

$(\operatorname{rot}\;\mathbf F)_y = \partial_z F_x - \partial_x F_z \equiv \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x}$

$(\operatorname{rot}\;\mathbf F)_z = \partial_x F_y - \partial_y F_x \equiv \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y}$

(что можно считать альтернативным определением, по сути совпадающим с определением в начале параграфа, по крайней мере при условии дифференцируемости компонент поля).

Для удобства можно формально представлять ротор как векторное произведение оператора набла (слева) и векторного поля:

$\operatorname{rot}\; \mathbf{F} = \mathbf{\nabla} \times \mathbf{F} = \begin{pmatrix} \frac{\partial}{\partial x} \\ \\ \frac{\partial}{\partial y} \\ \\ \frac{\partial}{\partial z} \end{pmatrix} \times \mathbf F = \begin{vmatrix} \mathbf{e}_x & \mathbf{e}_y & \mathbf{e}_z \\ \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ \\ F_x & F_y & F_z \end{vmatrix}.$

(Последнее равенство формально представляет векторное произведение как определитель).

Связанные определения

Векторное поле, ротор которого равен нулю в любой точке, называется безвихревым и является потенциальным. Поскольку эти условия являются друг для друга необходимыми и достаточными, оба термина являются практическими синонимами. (Впрочем, это верно только для случая полей, определённых на односвязной области).

Чуть подробнее о взаимной обусловленности потенциальности и безвихревого характера поля - см. ниже (Основные свойства).

Напротив, поле, ротор которого не равен нулю, называется обычно вихревым, такое поле не может быть потенциальным.

Обобщение

Наиболее прямое обобщение ротора применительно к векторным (и псевдовекторным) полям, определённым на пространствах произвольной размерности (при условии совпадения размерности пространства с размерностью вектора поля) такое

$(\operatorname{rot}\;\mathbf F)_{12} = \left(\frac{\partial F_2}{\partial x_1} - \frac{\partial F_1}{\partial x_2}\right)$

$(\operatorname{rot}\;\mathbf F)_{13} = \left(\frac{\partial F_3}{\partial x_1} - \frac{\partial F_1}{\partial x_3}\right)$

$(\operatorname{rot}\;\mathbf F)_{23} = \left(\frac{\partial F_3}{\partial x_2} - \frac{\partial F_2}{\partial x_3}\right)$

...

или

$(\operatorname{rot}\;\mathbf F)_{mn} = \partial_m F_n - \partial_n F_m \equiv \frac{\partial F_n}{\partial x_m} - \frac{\partial F_m}{\partial x_n}$

при индексах m и n от 1 до размерности пространства.

Это же может быть записано как внешнее произведение:

$\operatorname{rot}\;\mathbf F = \nabla \wedge \mathbf F.$

При этом ротор есть антисимметричное[5] тензорное поле валентности два.
В случае размерности 3 свертка этого тензора с символом Леви-Чивиты даёт обычное определение трехмерного ротора, приведённое в статье выше.
Для двумерного пространства может быть вдобавок при желании использована аналогичная формула с псевдоскалярным произведением (такой ротор будет псевдоскаляром, совпадающим с проекцией традиционного векторного произведения на ось, ортогональную данному двумерному пространству - если считать при этом двумерное пространство вложенным в некое трехмерное, чтобы традиционное векторное произведение имело смысл).

Физическая интерпретация

По теореме Коши-Гельмгольца распределение скоростей сплошной среды вблизи точки О задаётся уравнением

$\mathbf{v}(\mathbf{r}) = \mathbf{v}_{O} + \mathbf{\omega} \times \mathbf{r} + \nabla\varphi + o(\mathbf{r}),$

где $\mathbf{\omega}$ — вектор углового вращения элемента среды в точке О, а $\varphi$ — квадратичная форма от координат — потенциал деформации элемента среды.

Таким образом, движение сплошной среды вблизи точки О складывается из поступательного движения (вектор $\mathbf{v}_{O}$ ), вращательного движения (вектор $\mathbf{\omega} \times \mathbf{r}$ ) и потенциального движения — деформации (вектор $\nabla\varphi$ ). Применяя к формуле Коши—Гельмгольца операцию ротора, получим, что в точке О справедливо равенство $\operatorname{rot} ~\mathbf{v} = 2\mathbf{\omega},$ и, следовательно, можно заключить, что когда речь идет о векторном поле, являющемся полем скоростей некоторой среды, ротор этого векторного поля в заданной точке равен удвоенному вектору углового вращения элемента среды с центром в этой точке.

В качестве интуитивного образа, как это описано выше, здесь можно использовать представление о вращении брошенной в поток маленькой пылинки (увлекаемой потоком с собой, без его заметного возмущения) или о вращении помещённого в поток с закреплённой осью маленького (без инерции, вращаемого потоком, заметно не искажая его) колеса с прямыми (не винтовыми) лопастями. Если то или другое при взгляде на него вращается против часовой стрелки, то это означает, что вектор ротора поля скорости потока в данной точке имеет положительную проекцию в направлении на нас.

Основные свойства

Свойства, непосредственно получаемые из обычных правил дифференцирования

Линейность:

$\operatorname{rot}\;( a\mathbf{F} + b\mathbf{G} ) = a\;\operatorname{rot} ~\mathbf{F} + b\;\operatorname{rot} ~\mathbf{G}$

для любых векторных полей F и G и для любых постоянных чисел a и b.

Если $\varphi$ — скалярное поле, а F — векторное, тогда:

![\operatorname{rot} ~\varphi \mathbf{F} = \operatorname{grad} ~\varphi ~\times \mathbf{F}

\varphi ;\operatorname{rot} ~\mathbf{F}, ](https://dic.academic.ru/dic.nsf/ruwiki/c16b009d6c0fed6acd99f9a56661e64a.png)

или

![\nabla\times(\varphi \mathbf{F}) = (\nabla\varphi) \times \mathbf{F}

\varphi ;(\nabla\times\mathbf{F}). ](https://dic.academic.ru/dic.nsf/ruwiki/733576e82e754d6c199fa2516439b387.png)

Дивергенция ротора равна нулю:

$\operatorname{div} ~\operatorname{rot} ~\mathbf{F} = 0$ или $\nabla \cdot (\nabla \times \mathbf{F}) = 0 .$

При этом верно и обратное: если поле F бездивергентно, оно вихрь некоторого поля G (векторного потенциала):

$\operatorname{div} ~\mathbf{F} = 0 \Rightarrow \mathbf{F} = \operatorname{rot} ~\mathbf{G}.$

Если поле F потенциально, его ротор равен нулю (поле F — безвихревое):

$\mathbf{F} = \operatorname{grad}~\varphi \Rightarrow \operatorname{rot} ~\mathbf{F} = 0$

Верно и обратное: если поле безвихревое, то оно потенциально:

$\operatorname{rot} ~\mathbf{F} = 0 \Rightarrow \mathbf{F} = \operatorname{grad}~\varphi$

для некоторого скалярного поля $\varphi\$ (то есть найдется такое $\varphi\$ , что F будет его градиентом).

(Следствие из свойств выше): два (и сколько угодно) различных векторных поля могут иметь одинаковый ротор. При этом различаться они будут обязательно на безвихревое поле, то есть на градиент некоторого скалярного поля.
Ротор ротора равен градиенту дивергенции минус лапласиан:

$\operatorname{rot} ~\operatorname{rot} ~\mathbf{F} = \operatorname{grad} ~\operatorname{div} ~\mathbf{F} - \Delta\mathbf{F}$

Теорема Стокса

Циркуляция вектора по замкнутому контуру, являющемуся границей некоторой поверхности, равна потоку ротора этого вектора через эту поверхность:

$\oint\limits_{\partial S}\mathbf{F} \cdot\,\mathbf{dl} = \int\limits_S (\operatorname{rot} ~\mathbf{F}) \cdot \,\mathbf{dS}$

Частный случай теоремы Стокса для плоской поверхности - содержание теоремы Грина.

Альтернативные определения

Все определения ротора, о которых будет говориться в данном параграфе полностью эквивалентны (по крайней мере для случая дифференцируемого векторного поля), и в качестве основного, в принципе, можно выбрать любое из них. Остальные тогда оказываются формулами, которые могут быть более удобны в том или ином случае.

Прежде всего, перечислим явно те варианты, которые уже упоминались в статье выше и могут при желании каждое играть роль определения ротора.

Классическое определение, приведённое в данной статье как основное (см.Математическое определение).
Вычислительная формула через производные компонент в декартовых координатах, приведённая там же.
Формула в параграфе Физическая интерпретация.

Кроме них полезно упомянуть:

Выражение через символ Леви-Чивиты, дающее наиболее компактную координатную запись, а во втором варианте - общую формулу для любых криволинейных координат (ограничиваясь[6], правда, только размерностью 3):

где $g^{jm}$ - метрический тензор в представлении с верхними индексами. В последнем случае (общем) важно упомянуть, что под значком $\varepsilon_{ijk}$ имеется в виду именно тензор, включая множитель $\sqrt{g}.$

Интересную и довольно красивую форму определения, иногда используемую в литературе:

$\mathrm{rot}\ \mathbf a \Big|_{O} = \lim_{S\rightarrow O} \oint\limits_{S} [\mathbf a \times \mathbf{dS}].$

Ротор в криволинейных координатах

Общий случай

Удобным общим выражение ротора, пригодным для произвольных криволинейных координат в трехмерном[6] пространстве является выражение с использованием тензора Леви-Чивиты:

Используя верхние и нижние индексы и правило суммирования Эйнштейна:

$(\mathrm{rot}\ \mathbf v)_i = \varepsilon_{ijk}g^{jm}\frac{\partial}{\partial x^m} v^k,$

где $\varepsilon_{ijk}$ - координатная запись тензора Леви-Чивиты, включая множитель $\sqrt{g},$ $g^{jm}$ - метрический тензор в представлении с верхними индексами, $g \equiv \mathrm{det} (g_{rs}).$

Это выражение при желании может быть также переписано, например, в виде:

$(\mathrm{rot}\ \mathbf v)^n = g^{ni}\varepsilon_{ijk}g^{jm}\frac{\partial}{\partial x^m} v^k,$

итд.

В ортогональных криволинейных координатах

$\operatorname{rot}\;\mathbf{A} = \operatorname{rot}\;(\mathbf{q_1}A_1 + \mathbf{q_2}A_2 + \mathbf{q_3}A_3) =$

$= \frac{1}{H_2H_3}\left[\frac{\partial}{\partial q_2}(A_3H_3) - \frac{\partial}{\partial q_3}(A_2H_2)\right]\mathbf{q_1}\ +$

$+\ \frac{1}{H_3H_1}\left[\frac{\partial}{\partial q_3}(A_1H_1) - \frac{\partial}{\partial q_1}(A_3H_3)\right]\mathbf{q_2}\ +$

$+\ \frac{1}{H_1H_2}\left[\frac{\partial}{\partial q_1}(A_2H_2) - \frac{\partial}{\partial q_2}(A_1H_1)\right]\mathbf{q_3},$

где Hi — коэффициенты Ламе.

Примеры

В этой главе будем использовать для единичных векторов по осям (прямоугольных) декартовых координат использовать обозначение $\mathbf e_x, \mathbf e_y, \mathbf e_z.$

Простой пример

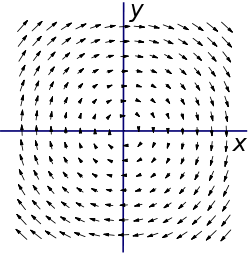
Рассмотрим векторное поле F, зависящее от координат x и y так:

$\mathbf{F}(x,y)=y\mathbf e_x - x \mathbf e_y$ .

В отношении этого примера нетрудно заметить, что $\mathbf{F} = \mathbf\omega \times \mathbf r$ , где r - радиус-вектор, а $\omega = -1 \mathbf e_z$ , то есть поле F можно рассматривать как поле скоростей точек твёрдого тела, вращающегося с единичной по величине угловой скоростью, направленной в отрицательном направлении оси z (то есть по часовой стрелке, если смотреть "сверху" - против оси z). Интуитивно более или менее очевидно, что поле закручено по часовой стрелке. Если мы поместим колесо с лопастями в жидкость, текущую с такими скоростями (то есть вращающуюся как целое по часовой стрелке), в любое место, мы увидим, что оно начнет вращаться по направлению часовой стрелки. (Для определения направлений используем, как обычно, правило правой руки или правого винта).
_z_-компоненту поля F будем считать равной нулю. Однако если она ненулевая, но постоянная (или даже зависящая только от z) - результат для ротора, получаемый ниже, будет тем же.

Вычислим ротор:

$\mathbf{\nabla} \times \mathbf{F} =0 \mathbf e_x + 0 \mathbf e_y+ \left[ {\frac{\partial}{\partial x}}(-x) -{\frac{\partial}{\partial y}} y \right] \mathbf e_z = -2\mathbf e_z$

Как и предположили, направление совпало с отрицательным направлением оси z. В данном случае ротор оказался константой, то есть поле $\mathbf{\nabla} \times \mathbf{F}$ оказалось однородным, не зависящим от координат (что естественно для вращения твёрдого тела). Что замечательно,

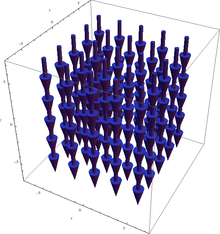
Угловая скорость вращения в данном примере одна и та же в любой точке пространства (угол поворота пылинки, приклеенной к твердому телу не зависит от того места, где именно приклеить пылинку). График ротора F поэтому не слишком интересен:

Более сложный пример

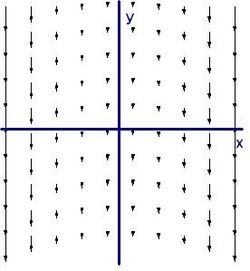
Теперь рассмотрим несколько более сложное векторное поле[7]:

$F(x,y)=-x^2 \mathbf e_y$ .

Его график:

Мы можем не увидеть никакого вращения, но, посмотрев повнимательнее направо, мы видим большее поле в, например, точке _x_=4, чем в точке _x_=3. Если бы мы установили маленькое колесо с лопастями там, больший поток на правой стороне заставил бы колесо вращаться по часовой стрелке, что соответствует ввинчиванию в направлении -z. Если бы мы расположили колесо в левой части поля, больший поток на его левой стороне заставил бы колесо вращаться против часовой стрелки, что соответствует ввинчиванию в направлении +z. Проверим нашу догадку с помощью вычисления:

$\mathbf{\nabla} \times \mathbf{F} = 0 \mathbf e_x + 0 \mathbf e_y + {\frac{\partial}{\partial x}}(-x^2) \mathbf e_z = -2x \mathbf e_z$

Действительно, ввинчивание происходит в направлении +z для отрицательных x и -z для положительных x, как и ожидалось. Так как этот ротор не одинаков в каждой точке, его график выглядит немного интереснее:

Ротор F с плоскостью x=0, выделенной тёмно-синим цветом

Можно заметить, что график этого ротора не зависит от y или z (как и должно быть) и направлен по -z для положительных x и в направлении +z для отрицательных x.

Три общих примера

Рассмотрим пример ∇ × [ v × F ]. Используя прямоугольную систему координат, можно показать, что

$\mathbf{ \nabla \times} \left( \mathbf{v \times F} \right) = \left[ \left( \mathbf{ \nabla \cdot F } \right) + \mathbf{F \cdot \nabla} \right] \mathbf{v}- \left[ \left( \mathbf{ \nabla \cdot v } \right) + \mathbf{v \cdot \nabla} \right] \mathbf{F} \ .$

Если v и ∇ поменять местами:

$\mathbf{v \ \times } \left( \mathbf{ \nabla \times F} \right) =\nabla_F \left( \mathbf{v \cdot F } \right) - \left( \mathbf{v \cdot \nabla } \right) \mathbf{ F} \ ,$

что является фейнмановской записью с нижним индексом ∇F, что значит, что градиент с индексом F относится только к F.

Другой пример ∇ × [ ∇ × F ]. Используя прямоугольную систему координат, можно показать, что:

$\nabla \times \left( \mathbf{\nabla \times F} \right) = \mathbf{\nabla} (\mathbf{\nabla \cdot F}) - \nabla^2 \mathbf{F} \ ,$

что можно считать частным случаем первого примера с подстановкой v → ∇.

Поясняющие примеры

В смерче ветры вращаются вокруг центра, и векторное поле скоростей ветра имеет ненулевой ротор (где-то) в центральной области. (см. Вихревое движение).
Для векторного поля v скоростей движения точек вращающегося твёрдого (абсолютно твёрдого) тела, rot v одинаков всюду по объёму этого тела и равен (вектору) удвоенной угловой скорости вращения (подробнее - см. выше).
Если бы скорости автомобилей на трассе описывались векторным полем, и разные полосы имели разные ограничения по скорости движения, ротор на границе между полосами был бы ненулевым.
Закон электромагнитной индукции Фарадея, одно из уравнений Максвелла, просто записывается (в дифференциальной форме) через ротор: ротор электрического поля равен скорости изменения магнитного поля (со временем), взятой с обратным знаком.
Четвёртое уравнение Максвелла - закон Ампера - Максвелла также записывается в дифференциальной форме с использованием ротора: ротор напряжённости магнитного поля равен сумме плотностей тока обычного и тока смещения.[8]

Важный контринтуитивный пример

Довольно важно иметь в виду, что в принципе (хотя и далеко не всегда) направление ротора может не соответствовать направлению вращения поля (будем говорить для конкретности о поле скоростей жидкости), которое кажется очевидным по направлению искривления линий тока. Он может даже иметь противоположное направление (а в частном случае ротор может оказаться равным нулю, хотя линии тока загибаются или даже представляют собой точные окружности).

Дело в том, что ротор может быть представлен как сумма двух слагаемых, одно из которых завивит от кривизны линий тока, а второе от завивимости скорости течения от перпендикулярной (в данной точке) скорости течения координаты.

Рассмотрим частный, но хорошо иллюстрирующий сказанное пример. Пусть поле скорости течения жидкости v таково, что на любом фиксированном расстоянии r от некоторого фиксированного центра (поместим туда для удобства и начало координат) - жидкость течет точно по окружности с центром в начале координат и радиусом r (будем для краткости говорить в двумерных терминах; для перехода к трехмерной формулировке этого примера надо заменить слово "центр" на слово "ось").

Пусть скорость движения по каждой такой окружности (равная абсолютной величине вектора v) зависит только от r :

$v \equiv |\mathbf v| = v(r).$

Пусть направление вращения - против часовой стрелки (угловая скорость - вдоль оси z).

Нам будет досаточно вычислить ротор только вдоль оси x. Для этого выразим v (его компоненты) через координаты вблизи оси x.

$v_x = - v(x) y / x,\$

$v_y = v(x).\$

(Учитывая то, что вблизи оси x можем считать, что координата y << x, а при дифференцировании нам нужен будет только первый порядок, мы отбросили всё, меньшее y/x, и воспользовались тем, что вследствии этого x≈r).

Вычислим теперь прямо компоненту ротора на ось z:

$(rot\ \mathbf v)_z = \partial_x v_y - \partial_y v_x,$

что даст, если подставить сюда v_x, v_y приведённые выше,

$(rot\ \mathbf v)_z = d v(x) / dx + v(x) / x.$

Отсюда видно, что

Если v(r) ~ 1/r, то rot v = 0.
Eсли v(r) убывает с r быстрее, чем 1/r, то проекция ротора на ось z отрицательна! (это и есть контринтуитивный пример).

Таким образом, мы видим, что в принципе просто из того, куда закручены линии тока не очевидно, куда направлен ротор такого течения. То есть не очевидно, в какую сторону будут вращаться пылинки в таком потоке. Зато достаточно ясно, что если где-то есть очень резкое убывание v(r), то направление ротора в этом месте будет направоено против того, которое соответствует направлению закручивания линий тока.

Этот частный пример означает, что и в общем случае однозначной связи между направлением закручивания линий поля и направлением вектора его ротора - нет.

Необходимо однако сделать две оговорки:

всё сказанное не означает, что однозначной связи между направлением закручивания линий поля и направлением вектора ротора этого поля не может быть для каких-то конкретных полей (подчиняющихся определённым уравнениям) и даже, быть может, для большинства практически важных полей в простых ситуациях. Однако если такая связь для каких-то (и даже для многих) полей имеет место, то
1. во-первых, это есть следствие не определения ротора, а других уравнений (которые могут быть справедливы для какого-то конкретного поля и какой-то конкретной ситуации, а могут - для других полей ситуаций - и не быть),
2. во-вторых, даже если эти другие уравнения в простейшем случае дадут такую связь, то при усложнении ситуации она может пропасть. Например, при переходе от случая однородной среды к неоднородной; так, даже если для однородной жидкости в бесконечном свободном пространстве такая связь имела бы место, то для вращения жидкости в неподвижном сосуде, скажем круглом стакане, очевидно вблизи стенок ротор будет противоположен направлению вращения жидкости в целом.
исходя из теоремы Стокса можно утверждать, что если (например) жидкость вращается по окружности, то где-то внутри этой окружности есть точки, в которых ротор имеет знак (направление), совпадающий с направлением циркуляции жидкости. В нашем примере быстроубывающего v(r), рассмотренном выше в этой главе, такая область находится вблизи центра (в предельном случае - в самом центре ротор даже становится бесконечным). Однако мы утверждаем (как это и видно из примера), что это совпадение не обязано существовать ни вблизи данной точки, ни даже везде внутри окружности данного радиуса (а лишь где-то внутри неё, хотя интеграл по всей её внутренности и даст таки это совпадение, то есть "в среднем" - направление совпадает; однако в большинстве точек - может быть и противоположным).

Примечания

↑ Также в немецкой, откуда, по-видимому, это обозначение и попало в русскую, а также почти везде в Европе, кроме Англии, где такое обозначение считается "альтернативным".
↑ Точнее - если F - псевдовекторное поле, то rot F - обычное векторное поле (вектор rot F - полярный), и наоборот, если поле F - поле обычного (полярного) вектора, то rot F - псевдовекторное поле.
↑ См. далее.
↑ Обычное соглашение, согласованное с определением через векторное произведение с оператором набла.
↑ То, что тензор антисимметричен, очевидно непосредственно из определения.
↑ 1 2 Для произвольной размерности - см. параграф «Обобщение».
↑ Простейшая физическая реализация такого поля (с точностью до аддитивной константы, которая не влияет на вычисление ротора, поскольку rot const = 0; кроме того, при желании эта константа может быть обнулена переходом в систему отсчета, связанной с максимально быстро текущей водой в центре струи) - ламинарное течение (вязкой) жидкости между двумя параллельными твердыми плоскостями, перпендикулярными оси х, под действием однородного силового поля (тяжести) или разности давлений. Течение жидкости в трубе круглого сечения даёт такую же зависимости , поэтому приведённое дальше вычисление ротора применимо и к этому случаю (проще всего взять ось y совпадающей с осью трубы, и хотя зависимость $\mathbf v (z)$ не будет уже константой, однако $\partial v_y/\partial z$ будет нулем при z = 0, как и в основном примере, т.е. вычисление и ответ для любой плоскости, проходящей через ось трубы такой же, а это решает задачу).
↑ Математический словарь высшей школы. В. Т. Воднев, А. Ф. Наумович, Н. Ф. Наумович