Целая часть | это... Что такое Целая часть? (original) (raw)

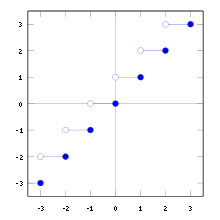
График функции «пол» (целая часть числа)

График функции «потолок»

В математике, целая часть вещественного числа — округление до ближайшего целого в меньшую сторону. Целая часть числа также называется антье (фр. entier), или пол (англ. floor). Наряду с полом существует парная функция — потолок (англ. ceiling) — округление до ближайшего целого в большую сторону.

Содержание

1 Обозначения и примеры
2 Определения
3 Свойства
4 Применение
5 В информатике
- 5.1 В языках программирования
- 5.2 В системах вёрстки
6 Примечания
7 См. также
8 Литература

Обозначения и примеры

Для целой части числа долгое время использовалось обозначение [x] , введенное Гауссом [источник не указан 1264 дня]. Ни понятия функции потолок, ни специального обозначения для нее не существовало. В 1962 году Кеннет Айверсон предложил округления числа до ближайшего целого в меньшую и большую стороны называть «пол» и «потолок» и обозначать $\lfloor x \rfloor$ и $\lceil x \rceil$ соответственно [1].

В современной математике используются оба обозначения, [x] и $\lfloor x \rfloor$ , однако существует тенденция перехода к терминологии и обозначениям Айверсона. Одна из причин этого — потенциальная неоднозначность понятия «целая часть числа»[1]. Например, целая часть числа 2,7 равна 2, но возможны два мнения на то, как определить целую часть числа −2,7. В соответствии с данным в этой статье определением $[x] \equiv \lfloor x \rfloor = -3$ , однако в некоторых калькуляторах имеется функция целой части числа INT, для отрицательных чисел определяемая как INT(-x) = -INT(x), так что INT(-2,7) = −2. В терминологии Айверсона отсутствуют возможные неоднозначности:

$\begin{matrix} \lfloor 2{,}7 \rfloor = 2, & \lfloor -2{,}7 \rfloor = -3, \\ \lceil 2{,}7 \rceil = 3, & \lceil -2{,}7 \rceil = -2 \end{matrix}$

Определения

Функция пол $\lfloor \, \cdot \, \rfloor\colon x \mapsto \lfloor x \rfloor$ определяется как наибольшее целое, меньшее или равное :

$\lfloor x \rfloor = \max\{ n \in \mathbb{Z} \mid n \leqslant x\}$

Функция потолок $\lceil \, \cdot \, \rceil\colon x \mapsto \lceil x \rceil$ определяется как наименьшее целое, большее или равное :

$\lceil x \rceil = \min\{ n \in \mathbb{Z} \mid n \geqslant x\}$

Эти определения эквивалентны следующим неравенствам (где n — целое число) [2]:

$\begin{align} \lfloor x \rfloor = n & \Longleftrightarrow & n \leqslant x < n+1 & \Longleftrightarrow & x-1 < n \leqslant x \\ \lceil x \rceil = n & \Longleftrightarrow & n-1 < x \leqslant n & \Longleftrightarrow & x \leqslant n < x+1. \end{align}$

Свойства

Везде ниже x, y обозначают вещественные числа, а n, m — целые.

Пол/потолок как функции вещественной переменной

Функции пол/потолок отображают множество вещественных чисел в множество целых чисел:

$\lfloor \, \cdot \, \rfloor\colon \mathbb{R} \to \mathbb{Z}, \quad \lceil \, \cdot \, \rceil\colon \mathbb{R} \to \mathbb{Z}, \quad$

Пол/потолок — кусочно-постоянные функции.

Функции пол/потолок имеют разрывны во всех целочисленных точках, это разрывы первого рода со скачком, равным единице.

При этом, функция пол является:

Функция потолок является:

Связь функций пола и потолка

Для произвольного [3]

$\lfloor x \rfloor \leqslant x \leqslant \lceil x \rceil$

Для целого пол и потолок совпадают:

$\lfloor x \rfloor = x \quad \Longleftrightarrow \quad x \in \mathbb{Z} \quad \Longleftrightarrow \quad \lceil x \rceil = x$

Если — не целое, то потолок ровно на единицу выше пола:

$\lceil x \rceil - \lfloor x \rfloor = \begin{cases} 1, & x \notin \mathbb{Z} \\ 0, & x \in \mathbb{Z} \end{cases}$

Функции пола и потолка являются отражениями друг друга от обеих осей:

$\lfloor -x \rfloor = -\lceil x \rceil, \quad \lceil -x \rceil = -\lfloor x \rfloor$

Пол/потолок: неравенства

Любое неравенство между вещественным и целым числами равносильно неравенству с полом и потолком между целыми числами [2]:

$\begin{matrix} n \leqslant x & \Longleftrightarrow & n \leqslant \lfloor x \rfloor & \qquad x \leqslant n & \Longleftrightarrow & \lceil x \rceil \leqslant n \\ n < x & \Longleftrightarrow & n < \lceil x \rceil & \qquad x < n & \Longleftrightarrow & \lfloor x \rfloor < n \end{matrix}$

Два верхних неравенства являются непосредственными следствиями определений пола и потолка, а два нижние — обращение верхних от противного.

Функции пол/потолок являются монотонно возрастающими функциями:

$x \leqslant y \Rightarrow \lfloor x \rfloor \leqslant \lfloor y \rfloor , \quad x \leqslant y \Rightarrow \lceil x \rceil \leqslant \lceil y \rceil$

Пол/потолок: сложение

Целочисленное слагаемое можно вносить/выносить за скобки пола/потолка [4]:

$\lfloor x + n \rfloor = \lfloor x \rfloor + n , \quad \lceil x + n \rceil = \lceil x \rceil + n$

Предыдущее равенство, вообще говоря, не выполняется, если оба слагаемых — вещественные числа. Однако и в этом случае справедливы неравенства:

$\lfloor x \rfloor + \lfloor y \rfloor \leqslant \lfloor x + y \rfloor \leqslant \lfloor x \rfloor + \lfloor y \rfloor + 1 , \quad \lceil x \rceil + \lceil y \rceil - 1 \leqslant \lceil x + y \rceil \leqslant \lceil x \rceil + \lceil y \rceil$

Пол/потолок под знаком функции

Имеет место следующее предложение:[5]

Пусть f(x) — непрерывная монотонно возрастающая функция, определенная на некотором промежутке, обладающая свойством:

$f(x) \in \mathbb{Z} \Rightarrow x \in \mathbb{Z}$

Тогда

$\lfloor f(x) \rfloor = \lfloor f(\lfloor x \rfloor) \rfloor, \quad \lceil f(x) \rceil = \lceil f(\lceil x \rceil) \rceil$

всякий раз, когда определены $f(x), f(\lfloor x \rfloor), f(\lceil x \rceil)$ .

В частности,

$\left \lfloor \frac{x+m}{n} \right \rfloor = \left \lfloor \frac{\left \lfloor x \right \rfloor + m}{n} \right \rfloor ,\quad \left \lceil \frac{x+m}{n} \right \rceil = \left \lceil \frac{\left \lceil x \right \rceil + m}{n} \right \rceil$

если и — целые числа, и n>0 .

Пол/потолок: суммы

Если m,n — целые числа, m>0 , то [6]

$n=\left\lfloor\frac{n}{m}\right\rfloor + \left\lfloor\frac{n+1}{m}\right\rfloor +\dots+\left\lfloor\frac{n+m-1}{m}\right\rfloor$

Вообще, если — произвольное вещественное число, а — целое положительное, то

$\lfloor mx \rfloor=\left\lfloor x\right\rfloor + \left\lfloor x+\frac{1}{m}\right\rfloor +\dots+\left\lfloor x+\frac{m-1}{m}\right\rfloor$

Имеет место более общее соотношение [7]:

$\sum_{0 \leqslant k < m} \left \lfloor \frac{nk+x}{m} \right \rfloor = d \left \lfloor \frac{x}{d} \right \rfloor + \frac{(m-1)(n-1)}{2} + \frac{d-1}{2}, \quad d=(m,n)$

Так как правая часть этого равенства симметрична относительно и , то справедлив следующий закон взаимности:

$\sum_{0 \leqslant k < m} \left \lfloor \frac{nk+x}{m} \right \rfloor = \sum_{0 \leqslant k < n} \left \lfloor \frac{mk+x}{n} \right \rfloor , \quad m, n>0$

Разложимость в ряд

Тривиальным образом функция Антье раскладывается в ряд с помощью функции Хевисайда:

$[x]=\sum_{i=-\infty}^{+\infty}i\left(\theta(x-i)-\theta(x-i-1)\right),$

где каждое слагаемое ряда создаёт характерные "ступеньки" функции. Этот ряд сходится абсолютно, однако ошибочное преобразование его слагаемых может привести к "упрощённому" ряду

$\sum_{i=-\infty}^{+\infty}\theta\left(x-i\right),$

который расходится.

Применение

Целочисленные функции пол/потолок находят широкое применение в дискретной математике и теории чисел. Ниже приведены некоторые примеры использования этих функций.

Количество цифр в записи числа

Количество цифр в записи целого положительного числа в позиционной системе счисления с основанием b равно [8]

$\lfloor \log_{b} n \rfloor + 1$

Округление

Ближайшее к целое число может быть определено по формуле

$(x) = \lfloor x + 0,5\rfloor$

Бинарная операция mod

Операция «остаток по модулю», обозначаемая $\mod$ , может быть определена с помощью функции пола следующим образом. Если x,y — произвольные вещественные числа, и $y \neq 0$ , то неполное частное от деления на равно

$\lfloor x/y \rfloor$ ,

а остаток

$x \, \bmod \, y = x - y \lfloor x/y \rfloor$

Дробная часть

Дробная часть вещественного числа по определению равна

$\{x\} = x \, \bmod \, 1 = x - \lfloor x \rfloor$

Количество целых точек промежутка

Требуется найти количество целых точек в замкнутом промежутке с концами $\alpha$ и $\beta$ , то есть количество целых чисел , удовлетворяющий неравенству

$\alpha \leqslant n \leqslant \beta$

В силу свойств пол/потолка, это неравенство равносильно

$\lceil \alpha \rceil \leqslant n \leqslant \lfloor \beta \rfloor$ .

Это есть точек в замкнутом промежутке с концами $\lceil \alpha \rceil$ и $\lfloor \beta \rfloor$ , равное $\lfloor \beta \rfloor - \lceil \alpha \rceil + 1$ .

Аналогично можно подсчитать количество целых точек в других типах промежутков. Сводка результатов приведена ниже [9].

$\#\{ n \in \mathbb{Z} \colon \alpha \leqslant n \leqslant \beta \} = \lfloor \beta \rfloor - \lceil \alpha \rceil + 1$

$\#\{ n \in \mathbb{Z} \colon \alpha \leqslant n < \beta \} = \lceil \beta \rceil - \lceil \alpha \rceil$

$\#\{ n \in \mathbb{Z} \colon \alpha < n \leqslant \beta \} = \lfloor \beta \rfloor - \lfloor \alpha \rfloor$

$\#\{ n \in \mathbb{Z} \colon \alpha < n < \beta \} = \lceil \beta \rceil - \lfloor \alpha \rfloor - 1$

(Через $\# M$ обозначена мощность множества ).

Первые три результата справедливы при всех $\alpha \leqslant \beta$ , а четвертый — только при $\alpha < \beta$ .

Теорема Рэлея о спектре

Пусть $\alpha$ и $\beta$ — положительные иррациональные числа, связанные соотношением [10]

$\frac {1} {\alpha} + \frac{1} {\beta} = 1.$

Тогда в ряду чисел

$\lfloor \alpha\rfloor, \lfloor \beta \rfloor, \lfloor 2\alpha\rfloor, \lfloor 2\beta \rfloor, \ldots, \lfloor m\alpha\rfloor, \lfloor m\beta \rfloor, \ldots$

каждое натуральное $n \in \mathbb{N}$ встречается в точности один раз. Иными словами, последовательности

$\{m\alpha \mid m \in \mathbb{N}\}$ и $\{m\beta \mid m \in \mathbb{N}\}$ ,

называемые последовательностями Бетти (англ.), образуют разбиение натурального ряда.[11]

В информатике

В языках программирования

Во многих языках программирования существуют встроенные функции пола/потолка floor(), ceil().

В системах вёрстки

В TeX (и LaTeX) для символов пола/потолка $\lfloor$ , $\rfloor$ , $\lceil$ , $\rceil$ существуют специальные команды: \lfloor, \rfloor, \lceil, \rceil. Поскольку wiki использует LaTeX для набора математических формул, то и в данной статье использованы именно эти команды.

Примечания

↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 88.
↑ 1 2 Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90.
↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 89.
↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 90-91.
↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 93.
↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 108.
↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 112-117.
↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 91.
↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 95-96.
↑ Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — С. 99-100.
↑ А. Баабабов «Пентиум» хорошо, а ум лучше // Квант. — 1999. — № 4. — С. 36-38.

См. также

Литература

Р. Грэхем, Д. Кнут, О. Паташник. Конкретная математика. — М.: «Мир», 1998. — 703 с. — ISBN 5-03-001793-3
М. К. Потапов, В. В. Александров, П. И. Пасиченко. Алгебра и начала анализа. — АО Столетие, 1996.