§25.11(i) Definition §25.11(ii) Graphics §25.11(iii) Representations by the Euler–Maclaurin Formula §25.11(iv) Series Representations §25.11(v) Special Values §25.11(vi) Derivatives §25.11(vii) Integral Representations §25.11(viii) Further Integral Representations §25.11(ix) Integrals §25.11(x) Further Series Representations §25.11(xi) Sums §25.11(xii) a-Asymptotic Behavior
The function ζ(s,a) was introduced in Hurwitz (1882 )and defined by the series expansion
25.11.1
ζ(s,a)=∑n=0∞1(n+a)s,
ℜs>1, a≠0,−1,−2,….
ⓘ Defines: ζ(s,a): Hurwitz zeta function Symbols: ℜ: real part ,n: nonnegative integer ,a: real or complex parameter ands: complex variable Keywords: definition Source: Apostol (1976 , p. 251) Referenced by: (25.11.11) ,(25.11.15) ,(25.11.17) ,(25.11.2) ,(25.11.3) ,(25.11.4) ,§25.11(i) ,(25.14.2) ,(8.15.2) Permalink: http://dlmf.nist.gov/25.11.E1 Encodings: TeX , pMML , png See also: Annotations for §25.11(i) ,§25.11 andCh.25
ζ(s,a) has a meromorphic continuation in the s-plane, its only singularity in ℂ being a simple pole at s=1 with residue 1. As a function of a, with s (≠1) fixed, ζ(s,a)is analytic in the half-plane ℜa>0. The Riemann zeta function is a special case:
For most purposes it suffices to restrict 0<ℜa≤1 because of the following straightforward consequences of (25.11.1 ):
25.11.4
ζ(s,a)=ζ(s,a+m)+∑n=0m−11(n+a)s,
m=1,2,3,….
ⓘ Symbols: ζ(s,a): Hurwitz zeta function ,m: nonnegative integer ,n: nonnegative integer ,a: real or complex parameter ands: complex variable Keywords: recurrence Proof sketch: Derivable from (25.11.1 ) by comparing its sum overn=0,…,m−1, m≥1, with its sum over n≥m. Permalink: http://dlmf.nist.gov/25.11.E4 Encodings: TeX , pMML , png See also: Annotations for §25.11(i) ,§25.11 andCh.25
Most references treat real a with 0<a≤1.
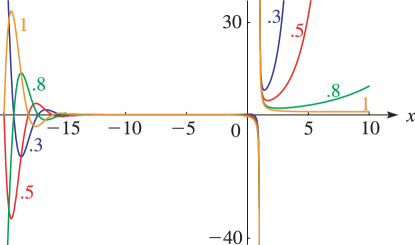
Figure 25.11.1: Hurwitz zeta function ζ(x,a),a = 0.3, 0.5, 0.8, 1, −20≤x≤10. The curves are almost indistinguishable for −14<x<−1, approximately.Magnify 3D Help
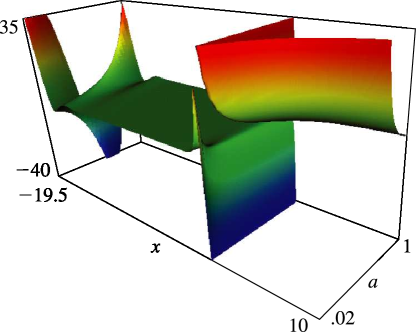
Figure 25.11.2: Hurwitz zeta function ζ(x,a),−19.5≤x≤10, 0.02≤a≤1.Magnify 3D Help
25.11.5
ζ(s,a)=∑n=0N1(n+a)s+(N+a)1−ss−1−s∫N∞x−⌊x⌋(x+a)s+1dx,
s≠1, ℜs>0, a>0, N=0,1,2,3,….
ⓘ Symbols: ζ(s,a): Hurwitz zeta function ,dx: differential of x ,⌊x⌋: floor of x ,∫: integral ,ℜ: real part ,n: nonnegative integer ,x: real variable ,a: real or complex parameter ands: complex variable Keywords: Euler–Maclaurin formula , improper integral Source: Apostol (1976 , (25), p. 269) Referenced by: (25.11.7) Permalink: http://dlmf.nist.gov/25.11.E5 Encodings: TeX , pMML , png See also: Annotations for §25.11(iii) ,§25.11 andCh.25
25.11.6
ζ(s,a)=1as(12+as−1)−s(s+1)2∫0∞B~2(x)−B2(x+a)s+2dx,
s≠1, ℜs>−1, a>0.
ⓘ Symbols: Bn: Bernoulli numbers ,ζ(s,a): Hurwitz zeta function ,dx: differential of x ,∫: integral ,B~n(x): periodic Bernoulli functions ,ℜ: real part ,x: real variable ,a: real or complex parameter ands: complex variable Keywords: Euler–Maclaurin formula , improper integral Source: Apostol (1985a , (25), p. 231) Referenced by: Erratum (V1.0.12) for Equations (25.11.6), (25.11.19), and (25.11.20) Permalink: http://dlmf.nist.gov/25.11.E6 Encodings: TeX , pMML , png Errata (effective with 1.0.12): Originally the integrand was incorrect because its numerator contained the functionB~2(x). The correct function is B~2(x)−B22.Reported 2016-05-08 by Clemens Heuberger See also: Annotations for §25.11(iii) ,§25.11 andCh.25
25.11.7
ζ(s,a)=1as+1(1+a)s(12+1+as−1)+∑k=1n(s+2k−22k−1)B2k2k1(1+a)s+2k−1−(s+2n2n+1)∫1∞B~2n+1(x)(x+a)s+2n+1dx,
s≠1, a>0, n=1,2,3,…, ℜs>−2n.
ⓘ Symbols: Bn: Bernoulli numbers ,ζ(s,a): Hurwitz zeta function ,(mn): binomial coefficient ,dx: differential of x ,∫: integral ,B~n(x): periodic Bernoulli functions ,ℜ: real part ,k: nonnegative integer ,n: nonnegative integer ,x: real variable ,a: real or complex parameter ands: complex variable Keywords: Euler–Maclaurin formula , improper integral Proof sketch: Derivable from (25.11.5 ) by setting N=1 and repeatedly integrating by parts using (1.2.6 ), (24.2.2 ), (24.2.4 ), (24.2.11 ), (24.2.12 ), (24.4.34 ). Permalink: http://dlmf.nist.gov/25.11.E7 Encodings: TeX , pMML , png See also: Annotations for §25.11(iii) ,§25.11 andCh.25
For B~n(x) see §24.2(iii) .
25.11.8
ζ(s,12a)=ζ(s,12a+12)+2s∑n=0∞(−1)n(n+a)s,
ℜs>0, s≠1, 0<a≤1.
ⓘ Symbols: ζ(s,a): Hurwitz zeta function ,ℜ: real part ,n: nonnegative integer ,a: real or complex parameter ands: complex variable Keywords: infinite series , series representation Source: Srivastava and Choi (2001 , (5), p. 89) Referenced by: (25.11.35) ,§25.11(x) Permalink: http://dlmf.nist.gov/25.11.E8 Encodings: TeX , pMML , png See also: Annotations for §25.11(iv) ,§25.11 andCh.25
25.11.9
ζ(1−s,a)=2Γ(s)(2π)s∑n=1∞1nscos(12πs−2nπa),
ℜs>0 if 0<a<1; ℜs>1 if a=1.
ⓘ Symbols: Γ(z): gamma function ,ζ(s,a): Hurwitz zeta function ,π: the ratio of the circumference of a circle to its diameter ,cosz: cosine function ,ℜ: real part ,n: nonnegative integer ,a: real or complex parameter ands: complex variable Keywords: infinite series , series representation Source: Apostol (1976 , (9), (10), p. 257) Referenced by: (25.13.3) ,Erratum (V1.1.4) for Equation (25.11.9) Permalink: http://dlmf.nist.gov/25.11.E9 Encodings: TeX , pMML , png Clarification (effective with 1.1.4): The constraint which originally read “ℜs>1, 0<a≤1” has been extended to be “ℜs>0 if 0<a<1; ℜs>1 if a=1”.Suggested 2021-08-23 by Gergő Nemes See also: Annotations for §25.11(iv) ,§25.11 andCh.25
25.11.10
ζ(s,a)=∑n=0∞(s)nn!ζ(n+s)(1−a)n,
s≠1, |a−1
<1.
ⓘ Symbols: Γ(z): gamma function ,ζ(s,a): Hurwitz zeta function ,(a)n: Pochhammer’s symbol (or shifted factorial) ,ζ(s): Riemann zeta function ,!: factorial (as in n!) ,n: nonnegative integer ,a: real or complex parameter ,s: complex variable andz: complex variable Keywords: infinite series , series representation Proof sketch: Derivable using Taylor’s theorem (1.10.1 ) with z=a, z0=1, (25.11.17 ), (5.2.4 ), (25.11.2 ). Referenced by: §25.11(iv) ,§25.11(iv) ,Erratum (V1.0.9) for Chapters 7, 25 Permalink: http://dlmf.nist.gov/25.11.E10 Encodings: TeX , pMML , png Notational Change (effective with 1.0.9): We have rewritten the original summation∑n=0∞Γ(n+s)n!Γ(s)ζ(n+s)(1−a)nmore concisely as ∑n=0∞(s)nn!ζ(n+s)(1−a)n using the Pochhammer symbol. See also: Annotations for §25.11(iv) ,§25.11 andCh.25
When a=12, (25.11.10 ) reduces to (25.8.3 ); compare (25.11.11 ).
For other series expansions similar to (25.11.10 ) see Coffey (2008 ).
Throughout this subsection ℜa>0.
25.11.12
ζ(n+1,a)=(−1)n+1ψ(n)(a)n!,
n=1,2,3,….
ⓘ Symbols: ζ(s,a): Hurwitz zeta function ,ψ(z): psi (or digamma) function ,!: factorial (as in n!) ,n: nonnegative integer anda: real or complex parameter Keywords: special value Source: Erdélyi et al. (1953a , (1.11.8), p. 29) Permalink: http://dlmf.nist.gov/25.11.E12 Encodings: TeX , pMML , png See also: Annotations for §25.11(v) ,§25.11 andCh.25
25.11.14
ζ(−n,a)=−Bn+1(a)n+1,
n=0,1,2,….
ⓘ Symbols: Bn(x): Bernoulli polynomials ,ζ(s,a): Hurwitz zeta function ,n: nonnegative integer anda: real or complex parameter Keywords: special value Source: Apostol (1976 , (17), p. 264) Permalink: http://dlmf.nist.gov/25.11.E14 Encodings: TeX , pMML , png See also: Annotations for §25.11(v) ,§25.11 andCh.25
25.11.15
ζ(s,ka)=k−s∑n=0k−1ζ(s,a+nk),
s≠1, k=1,2,3,….
ⓘ Symbols: ζ(s,a): Hurwitz zeta function ,k: nonnegative integer ,m: nonnegative integer ,n: nonnegative integer ,a: real or complex parameter ands: complex variable Keywords: special value Proof sketch: Derivable by starting with (25.11.1 ), replacinga↦ka, pulling out a factor of k−s and performing a change of sum index n=km+l with m≥0 and 0≤l≤k−1, which through Euclidean division converts the single sum into a double sum of the correct form. Referenced by: (25.11.24) Permalink: http://dlmf.nist.gov/25.11.E15 Encodings: TeX , pMML , png See also: Annotations for §25.11(v) ,§25.11 andCh.25
25.11.16
ζ(1−s,hk)=2Γ(s)(2πk)s∑r=1kcos(πs2−2πrhk)ζ(s,rk),
s≠0,1; h,k integers, 1≤h≤k.
ⓘ Symbols: Γ(z): gamma function ,ζ(s,a): Hurwitz zeta function ,π: the ratio of the circumference of a circle to its diameter ,cosz: cosine function ,k: nonnegative integer ands: complex variable Keywords: special value Source: Apostol (1976 , (14), p. 261) Referenced by: (25.11.21) Permalink: http://dlmf.nist.gov/25.11.E16 Encodings: TeX , pMML , png See also: Annotations for §25.11(v) ,§25.11 andCh.25
25.11.17
∂∂aζ(s,a)=−sζ(s+1,a),
s≠0,1; ℜa>0.
ⓘ Symbols: ζ(s,a): Hurwitz zeta function ,∂f∂x: partial derivative of f with respect to x ,∂x: partial differential of x ,ℜ: real part ,a: real or complex parameter ands: complex variable Keywords: derivative Proof sketch: Derivable by differentiating (25.11.1 ) with respect to a. Referenced by: (25.11.10) Permalink: http://dlmf.nist.gov/25.11.E17 Encodings: TeX , pMML , png See also: Annotations for §25.11(vi) ,§25.11(vi) ,§25.11 andCh.25
In (25.11.18 )–(25.11.24 ) primes on ζdenote derivatives with respect to s. Similarly in §§25.11(viii) and 25.11(xii) .
25.11.18
ζ′(0,a)=lnΓ(a)−12ln(2π),
a>0.
ⓘ Symbols: Γ(z): gamma function ,ζ(s,a): Hurwitz zeta function ,π: the ratio of the circumference of a circle to its diameter ,lnz: principal branch of logarithm function anda: real or complex parameter Keywords: derivative Source: Erdélyi et al. (1953a , (1.10.10), p. 26) Referenced by: §25.11(vi) Permalink: http://dlmf.nist.gov/25.11.E18 Encodings: TeX , pMML , png See also: Annotations for §25.11(vi) ,§25.11(vi) ,§25.11 andCh.25
25.11.19
ζ′(s,a)=−lnaas(12+as−1)−a1−s(s−1)2+s(s+1)2∫0∞(B~2(x)−B2)ln(x+a)(x+a)s+2dx−(2s+1)2∫0∞B~2(x)−B2(x+a)s+2dx,
ℜs>−1, s≠1, a>0.
ⓘ Symbols: Bn: Bernoulli numbers ,ζ(s,a): Hurwitz zeta function ,dx: differential of x ,∫: integral ,lnz: principal branch of logarithm function ,B~n(x): periodic Bernoulli functions ,ℜ: real part ,x: real variable ,a: real or complex parameter ,s: complex variable andk: integer Keywords: derivative Source: Apostol (1985a , fourth equation, p. 231); with k=1, φ2(x)=12(B~2(x)−B2) Referenced by: Erratum (V1.0.12) for Equations (25.11.6), (25.11.19), and (25.11.20) Permalink: http://dlmf.nist.gov/25.11.E19 Encodings: TeX , pMML , png Errata (effective with 1.0.12): Originally both integrands were incorrect because their numerators contained the functionB~2(x). The correct function is B~2(x)−B22.Reported 2016-06-27 by Gergő Nemes See also: Annotations for §25.11(vi) ,§25.11(vi) ,§25.11 andCh.25
25.11.20
(−1)kζ(k)(s,a)=(lna)kas(12+as−1)+k!a1−s∑r=0k−1(lna)rr!(s−1)k−r+1−s(s+1)2∫0∞(B~2(x)−B2)(ln(x+a))k(x+a)s+2dx+k(2s+1)2∫0∞(B~2(x)−B2)(ln(x+a))k−1(x+a)s+2dx−k(k−1)2∫0∞(B~2(x)−B2)(ln(x+a))k−2(x+a)s+2dx,
ℜs>−1, s≠1, a>0.
ⓘ Symbols: Bn: Bernoulli numbers ,ζ(s,a): Hurwitz zeta function ,dx: differential of x ,!: factorial (as in n!) ,∫: integral ,lnz: principal branch of logarithm function ,B~n(x): periodic Bernoulli functions ,ℜ: real part ,x: real variable ,a: real or complex parameter ,s: complex variable andk: integer Keywords: derivative Source: Apostol (1985a , fourth equation, p. 231); with φ2(x)=12(B~2(x)−B2) Referenced by: Erratum (V1.0.12) for Equations (25.11.6), (25.11.19), and (25.11.20) Permalink: http://dlmf.nist.gov/25.11.E20 Encodings: TeX , pMML , png Errata (effective with 1.0.12): Originally all three integrands were incorrect because their numerators contained the functionB~2(x). The correct function is B~2(x)−B22.Reported 2016-06-27 by Gergő Nemes See also: Annotations for §25.11(vi) ,§25.11(vi) ,§25.11 andCh.25
25.11.21
ζ′(1−2n,hk)=(ψ(2n)−ln(2πk))B2n(h/k)2n−(ψ(2n)−ln(2π))B2n2nk2n+(−1)n+1π(2πk)2n∑r=1k−1sin(2πrhk)ψ(2n−1)(rk)+(−1)n+12⋅(2n−1)!(2πk)2n∑r=1k−1cos(2πrhk)ζ′(2n,rk)+ζ′(1−2n)k2n,
where h,k are integers with 1≤h≤k and n=1,2,3,….
25.11.22
ζ′(1−2n,12)=−B2nln2n⋅4n−(22n−1−1)ζ′(1−2n)22n−1,
n=1,2,3,….
ⓘ Symbols: Bn: Bernoulli numbers ,ζ(s,a): Hurwitz zeta function ,ζ(s): Riemann zeta function ,lnz: principal branch of logarithm function andn: nonnegative integer Keywords: derivative Source: Miller and Adamchik (1998 , (17), p. 205) Permalink: http://dlmf.nist.gov/25.11.E22 Encodings: TeX , pMML , png See also: Annotations for §25.11(vi) ,§25.11(vi) ,§25.11 andCh.25
25.11.23
ζ′(1−2n,13)=−π(9n−1)B2n8n3(32n−1−1)−B2nln34n⋅32n−1−(−1)nψ(2n−1)(13)23(6π)2n−1−(32n−1−1)ζ′(1−2n)2⋅32n−1,
n=1,2,3,….
ⓘ Symbols: Bn: Bernoulli numbers ,ζ(s,a): Hurwitz zeta function ,ζ(s): Riemann zeta function ,π: the ratio of the circumference of a circle to its diameter ,ψ(z): psi (or digamma) function ,lnz: principal branch of logarithm function andn: nonnegative integer Keywords: derivative Source: Miller and Adamchik (1998 , (18), p. 205) Permalink: http://dlmf.nist.gov/25.11.E23 Encodings: TeX , pMML , png See also: Annotations for §25.11(vi) ,§25.11(vi) ,§25.11 andCh.25
25.11.24
∑r=1k−1ζ′(s,rk)=(ks−1)ζ′(s)+ksζ(s)lnk,
s≠1, k=1,2,3,….
ⓘ Symbols: ζ(s,a): Hurwitz zeta function ,ζ(s): Riemann zeta function ,lnz: principal branch of logarithm function ,a: real or complex parameter ,s: complex variable andk: integer Keywords: derivative Proof sketch: Derivable from (25.11.15 ) with a=1/k, multiplying by ks, differentiating with respect to s, and using (25.11.2 ). Referenced by: (25.11.21) ,§25.11(vi) Permalink: http://dlmf.nist.gov/25.11.E24 Encodings: TeX , pMML , png See also: Annotations for §25.11(vi) ,§25.11(vi) ,§25.11 andCh.25
25.11.25
ζ(s,a)
=1Γ(s)∫0∞xs−1e−ax1−e−xdx,
ℜs>1, ℜa>0.
ⓘ Symbols: Γ(z): gamma function ,ζ(s,a): Hurwitz zeta function ,dx: differential of x ,e: base of natural logarithm ,∫: integral ,ℜ: real part ,x: real variable ,a: real or complex parameter ands: complex variable Keywords: improper integral , integral representation Sources: Srivastava and Choi (2001 , (2), p. 89); Apostol (1976 , (5), p. 251) Referenced by: (25.11.27) ,(25.11.30) ,(25.11.35) ,§25.11(x) Permalink: http://dlmf.nist.gov/25.11.E25 Encodings: TeX , pMML , png See also: Annotations for §25.11(vii) ,§25.11 andCh.25
25.11.26
ζ(s,a)
=−s∫−a∞x−⌊x⌋−12(x+a)s+1dx,
−1<ℜs<0, 0<a≤1.
ⓘ Symbols: ζ(s,a): Hurwitz zeta function ,dx: differential of x ,⌊x⌋: floor of x ,∫: integral ,ℜ: real part ,x: real variable ,a: real or complex parameter ands: complex variable Keywords: improper integral , integral representation Source: Berndt (1972 , (5.3), p. 156) Permalink: http://dlmf.nist.gov/25.11.E26 Encodings: TeX , pMML , png See also: Annotations for §25.11(vii) ,§25.11 andCh.25
25.11.27
ζ(s,a)=12a−s+a1−ss−1+1Γ(s)∫0∞(1ex−1−1x+12)xs−1e−axdx,
ℜs>−1, s≠1, ℜa>0.
ⓘ Symbols: Γ(z): gamma function ,ζ(s,a): Hurwitz zeta function ,dx: differential of x ,e: base of natural logarithm ,∫: integral ,ℜ: real part ,x: real variable ,a: real or complex parameter ands: complex variable Keywords: improper integral , integral representation Proof sketch: Derivable from (25.11.25 ) by first rewriting(1−e−x)=e−x(ex−1), then replacingxs−1↦xs−1(1+e−x−e−x), using the identity e−x=(1−e−x)/(ex−1), and replacing(ex−1)−1↦((ex−1)−1−1/x+1/2−1/2+1/x) in the resulting integrand with (5.2.1 ), (5.5.1 ). Referenced by: (25.11.28) Permalink: http://dlmf.nist.gov/25.11.E27 Encodings: TeX , pMML , png Update (effective with 1.1.9): The fraction in the integrand xs−1eax was rewritten to read xs−1e−ax. See also: Annotations for §25.11(vii) ,§25.11 andCh.25
25.11.28
ζ(s,a)=12a−s+a1−ss−1+∑k=1nB2k(2k)!(s)2k−1a1−s−2k+1Γ(s)∫0∞(1ex−1−1x+12−∑k=1nB2k(2k)!x2k−1)xs−1e−axdx,
ℜs>−(2n+1), s≠1, ℜa>0.
ⓘ Symbols: Bn: Bernoulli numbers ,O(x): order not exceeding ,Γ(z): gamma function ,ζ(s,a): Hurwitz zeta function ,(a)n: Pochhammer’s symbol (or shifted factorial) ,dx: differential of x ,e: base of natural logarithm ,!: factorial (as in n!) ,∫: integral ,ℜ: real part ,k: nonnegative integer ,n: nonnegative integer ,x: real variable ,a: real or complex parameter ands: complex variable Keywords: improper integral , integral representation Proof sketch: Derivable from (25.11.27 ) by adding and subtracting∑k=1nB2kx2k−1/(2k)! in the integrand, using (5.2.1 ), (5.2.5 ), and recognizing that(ex−1)−1−x−1+1/2−∑k=1nB2kx2k−1/(2k)!=O(x2n+1)as x→0, demonstrating the region of convergence. Referenced by: Erratum (V1.0.9) for Chapters 7, 25 Permalink: http://dlmf.nist.gov/25.11.E28 Encodings: TeX , pMML , png Notational Change (effective with 1.0.9): We have rewritten the original summation∑k=1nΓ(s+2k−1)Γ(s)B2k(2k)!a−2k−s+1more concisely as ∑k=1nB2k(2k)!(s)2k−1a1−s−2kusing the Pochhammer symbol. See also: Annotations for §25.11(vii) ,§25.11 andCh.25
25.11.29
ζ(s,a)=12a−s+a1−ss−1+2∫0∞sin(sarctan(x/a))(a2+x2)s/2(e2πx−1)dx,
s≠1, ℜa>0.
ⓘ Symbols: ζ(s,a): Hurwitz zeta function ,π: the ratio of the circumference of a circle to its diameter ,dx: differential of x ,e: base of natural logarithm ,∫: integral ,arctanz: arctangent function ,ℜ: real part ,sinz: sine function ,x: real variable ,a: real or complex parameter ands: complex variable Keywords: improper integral , integral representation Source: Erdélyi et al. (1953a , (1.10.7), p. 26) Permalink: http://dlmf.nist.gov/25.11.E29 Encodings: TeX , pMML , png See also: Annotations for §25.11(vii) ,§25.11 andCh.25
25.11.30
ζ(s,a)=Γ(1−s)2πi∫−∞(0+)eazzs−11−ezdz,
s≠1, ℜa>0,
ⓘ Symbols: Γ(z): gamma function ,ζ(s,a): Hurwitz zeta function ,π: the ratio of the circumference of a circle to its diameter ,dx: differential of x ,e: base of natural logarithm ,i: imaginary unit ,∫: integral ,ℜ: real part ,a: real or complex parameter ,s: complex variable andz: complex variable Keywords: contour integral , integral representation Source: Erdélyi et al. (1953a , (1.10.5), p. 25); with z=−t Proof sketch: This contour integral uses Hankel’s contour Figure 5.9.1 . Assume ℜs>1, collapse the integration path onto the negative real axis, apply (25.11.25 ), followed by analytic continuation for all s≠1, ℜa>0, since the integrand is analytic in z, the convergence at the ends of the path is exponential for all s≠−1 and the Hankel contour can be kept well clear of the singularity at the origin in the z-plane. Referenced by: §25.11(i) ,§25.11(vii) ,Erratum (V1.2.1) for Figure 5.9.1 Permalink: http://dlmf.nist.gov/25.11.E30 Encodings: TeX , pMML , png See also: Annotations for §25.11(vii) ,§25.11 andCh.25
where the integration contour (see Figure 5.9.1 ) is a loop around the negative real axis as described for (25.5.20 ).
25.11.31
1Γ(s)∫0∞xs−1e−ax2coshxdx=4−s(ζ(s,14+14a)−ζ(s,34+14a)),
ℜs>0, ℜa>−1.
ⓘ Symbols: Γ(z): gamma function ,ζ(s,a): Hurwitz zeta function ,dx: differential of x ,e: base of natural logarithm ,coshz: hyperbolic cosine function ,∫: integral ,ℜ: real part ,x: real variable ,a: real or complex parameter ands: complex variable Keywords: improper integral , integral representation Proof sketch: The improper integral can be evaluated by using2coshx=ex(1+e−2x), changing variables 2x=t, and then applying (25.11.35 ). Permalink: http://dlmf.nist.gov/25.11.E31 Encodings: TeX , pMML , png See also: Annotations for §25.11(viii) ,§25.11 andCh.25
25.11.32
∫0axnψ(x)dx=(−1)n−1ζ′(−n)+(−1)nHnBn+1n+1−∑k=0n(−1)k(nk)HkBk+1(a)k+1an−k+∑k=0n(−1)k(nk)ζ′(−k,a)an−k,
n=1,2,…, ℜa>0,
ⓘ Symbols: Bn: Bernoulli numbers ,ζ(s,a): Hurwitz zeta function ,ζ(s): Riemann zeta function ,(mn): binomial coefficient ,dx: differential of x ,ψ(z): psi (or digamma) function ,Hn: harmonic number ,∫: integral ,ℜ: real part ,k: nonnegative integer ,n: nonnegative integer ,x: real variable ,a: real or complex parameter andh(n): harmonic number Keywords: definite integral , integral representation Source: Adamchik (1998 , (17), p. 197) Referenced by: Erratum (V1.1.4) for Notation Permalink: http://dlmf.nist.gov/25.11.E32 Encodings: TeX , pMML , png Notation (effective with 1.1.4): The notation previously used for the harmonic number h(n) (resp. h(k)) has been replaced to be Hn (resp. Hk).Suggested 2021-08-23 by Gergő Nemes See also: Annotations for §25.11(viii) ,§25.11 andCh.25
where Hn are the harmonic numbers :
25.11.34
n∫0aζ′(1−n,x)dx=ζ′(−n,a)−ζ′(−n)+Bn+1−Bn+1(a)n(n+1),
n=1,2,…, ℜa>0.
ⓘ Symbols: Bn: Bernoulli numbers ,Bn(x): Bernoulli polynomials ,ζ(s,a): Hurwitz zeta function ,ζ(s): Riemann zeta function ,dx: differential of x ,∫: integral ,ℜ: real part ,n: nonnegative integer ,x: real variable anda: real or complex parameter Keywords: definite integral , integral representation Source: Adamchik (1998 , (15), p. 196) Permalink: http://dlmf.nist.gov/25.11.E34 Encodings: TeX , pMML , png See also: Annotations for §25.11(viii) ,§25.11 andCh.25
See Prudnikov et al. (1990 , §2.3), Prudnikov et al. (1992a , §3.2), andPrudnikov et al. (1992b , §3.2).
25.11.35
∑n=0∞(−1)n(n+a)s=1Γ(s)∫0∞xs−1e−ax1+e−xdx=2−s(ζ(s,12a)−ζ(s,12(1+a))),
ℜa>0, ℜs>0; orℜa=0, ℑa≠0,0<ℜs<1.
ⓘ Symbols: Γ(z): gamma function ,ζ(s,a): Hurwitz zeta function ,dx: differential of x ,e: base of natural logarithm ,ℑ: imaginary part ,∫: integral ,ℜ: real part ,n: nonnegative integer ,x: real variable ,a: real or complex parameter ands: complex variable Keywords: improper integral , infinite series , integral representation , series representation Proof sketch: The infinite series connection to the difference of Hurwitz zeta functions is a restatement of (25.11.8 ). The integral representation is derivable from the difference of Hurwitz zeta functions by substituting (25.11.25 ) in each, making a change of variables x=2t, factoring, and expressing 1−e−2t=(1+e−t)(1−e−t). Referenced by: (25.11.31) ,§25.11(x) ,§25.11(x) Permalink: http://dlmf.nist.gov/25.11.E35 Encodings: TeX , pMML , png See also: Annotations for §25.11(x) ,§25.11 andCh.25
See also (8.15.2 ) and Srivastava and Choi (2001 ).
25.11.37
∑k=1∞(−1)kkζ(nk,a)=−nlnΓ(a)+ln(∏j=0n−1Γ(a−e(2j+1)πi/n)),
n=2,3,4,…, ℜa≥1.
ⓘ Symbols: Γ(z): gamma function ,ζ(s,a): Hurwitz zeta function ,π: the ratio of the circumference of a circle to its diameter ,e: base of natural logarithm ,i: imaginary unit ,lnz: principal branch of logarithm function ,ph: phase ,ℜ: real part ,k: nonnegative integer ,n: nonnegative integer anda: real or complex parameter Keywords: infinite series , series representation Source: Adamchik and Srivastava (1998 , (2.12), p. 136); with the choice ph(−1)=π, which is reasonable since the gamma function is single valued Permalink: http://dlmf.nist.gov/25.11.E37 Encodings: TeX , pMML , png See also: Annotations for §25.11(xi) ,§25.11 andCh.25
25.11.38
∑k=1∞(n+kk)ζ(n+k+1,a)zk=(−1)nn!(ψ(n)(a)−ψ(n)(a−z)),
n=1,2,3,…, ℜa>0, |z
<
ⓘ Symbols: ζ(s,a): Hurwitz zeta function ,(mn): binomial coefficient ,ψ(z): psi (or digamma) function ,!: factorial (as in n!) ,ℜ: real part ,k: nonnegative integer ,n: nonnegative integer ,a: real or complex parameter andz: complex variable Keywords: infinite series , series representation Source: Adamchik and Srivastava (1998 , (2.29), p. 138) Permalink: http://dlmf.nist.gov/25.11.E38 Encodings: TeX , pMML , png See also: Annotations for §25.11(xi) ,§25.11 andCh.25
25.11.39
∑k=2∞k2kζ(k+1,34)=8G,
where G is Catalan’s constant :
For further sums see Prudnikov et al. (1990 , pp. 396–397) andHansen (1975 , pp. 358–360).
As a→0 with s (≠1) fixed,
25.11.41
ζ(s,a+1)=ζ(s)−sζ(s+1)a+O(a2).
As β→±∞ with s fixed, ℜs>1,
uniformly with respect to bounded nonnegative values of α.
As a→∞ in the sector |pha|≤π−δ(<π), withs(≠1) and δ fixed, we have the asymptotic expansion
25.11.43
ζ(s,a)−a1−ss−1−12a−s∼∑k=1∞B2k(2k)!(s)2k−1a1−s−2k.
Similarly, as a→∞ in the sector|pha|≤π−δ(<π).
25.11.44
ζ′(−1,a)−112+14a2−(112−12a+12a2)lna∼−∑k=1∞B2k+2(2k+2)(2k+1)2ka−2k,
and
25.11.45
ζ′(−2,a)−112a+19a3−(16a−12a2+13a3)lna∼∑k=1∞2B2k+2(2k+2)(2k+1)2k(2k−1)a−(2k−1).
For the more general case ζ′(−m,a),m=1,2,…, see Elizalde (1986 ). For error bounds for (25.11.43 ), (25.11.44 ) and (25.11.45 ), see Nemes (2017a ).
For an exponentially-improved form of (25.11.43 ) seeParis (2005b ).