Ряд (математика) | это... Что такое Ряд (математика)? (original) (raw)

Ряд (математика)

Сумма ряда, или бесконе́чная су́мма, или ряд, — математическое выражение, позволяющее записать бесконечное количество слагаемых и подразумевающее значение их суммы, которое можно получить в предельном смысле. Если значение суммы (в предельном смысле) существует, то говорят, что ряд сходится. В противном случае говорят, что он расходится.

Определение

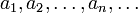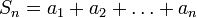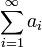Пусть $a_1,a_2,\ldots,a_n,\ldots$ — последовательность чисел. Число $S_n=a_1+a_2+\ldots+a_n$ называется _n-ой частичной суммой ряда $\sum_{i=1}^\infty a_i$ .

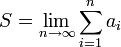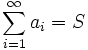Сумма (числового) ряда — это предел частичных сумм S n, если он существует и конечен. Таким образом, если существует число $S=\lim_{n\to\infty}\sum_{i=1}^{n}a_i$ , то в этом случае пишут $\sum_{i=1}^{\infty}a_i=S$ .

Сходимость

Если ряд сходится, то общий член ряда стремится к нулю. Достаточные признаки сложнее:

Примеры

См. также

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Ряд (математика)" в других словарях:

МАТЕМАТИКА — наука, или группа наук, о познаваемых разумом многообразиях и структурах, специально – о математических множествах и величинах; напр., элементарная математика – наука о числовых величинах (арифметика) и величинах пространственных (геометрия) и о… … Философская энциклопедия
Ряд Тейлора — Ряд Тейлора разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Брука Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора его использовали ещё в XVII веке Грегори, а… … Википедия
Ряд Маклорена — Ряд Тейлора разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора его использовали ещё в XVII веке Грегори, а также Ньютон. Ряды… … Википедия
Ряд тейлора — разложение функции в бесконечную сумму степенных функций. Ряд назван в честь английского математика Тейлора, хотя ряд Тейлора был известен задолго до публикаций Тейлора его использовали ещё в XVII веке Грегори, а также Ньютон. Ряды Тейлора… … Википедия
Ряд Винера — Ряд Винера это ортогональное разложение для нелинейных функционалов, тесно связанное с рядом Вольтерра и имеющее такое же отношение к нему, как ортогональное полиномиальное разложение к степенному ряду. Ряд Винера это дискретный аналог ряда … Википедия
Ряд Лорана — Ряд Лорана двусторонне бесконечный степенной ряд по целым степеням , то есть ряд вида Этот ряд понимается как сумма двух рядов: положительная часть ряда Лорана (иногда называется правильной) и отрицательная часть ряда Лорана… … Википедия
Ряд Штурма — (система Штурма) для вещественного многочлена последовательность многочленов, позволяющая эффективно определять количество корней многочлена на промежутке и приближённо вычислять их с помощью теоремы Штурма. Ряд и теорема названы именем… … Википедия
Ряд штурма — (система Штурма) для вещественного многочлена последовательность многочленов, позволяющая эффективно определять количество корней многочлена на промежутке и приближённо вычислять их с помощью теоремы Штурма. Ряд и теорема названы именем… … Википедия
Ряд Пюизё — (дробно степенной ряд) обобщение понятия степенного ряда, в котором используются не только целые, но и дробные (рациональные) показатели; допускаются также отрицательные показатели. Ряды Пюизё находят применение в различных разделах математики, в … Википедия
Ряд Лейбница — знакочередующийся ряд, названный именем исследовавшего его немецкого математика Лейбница: Как доказал Лейбниц, сумма этого ряда равна … Википедия