Формула Стокса | это... Что такое Формула Стокса? (original) (raw)

Формула Стокса

Формула Стокса

Теорема Стокса — одна из основных теорем дифференциальной геометрии и математического анализа об интегрировании дифференциальных форм, которая обобщает несколько теорем анализа. Названа в честь Дж. Г. Стокса.

Содержание

Общая формулировка

Пусть на ориентируемом многообразии M размерности n заданы ориентируемое _p_-мерное подмногообразие σ и дифференциальная форма ω степени _p_−1 класса C1 (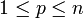1\leq p \leq n). Тогда если граница подмногообразия ∂σ положительно ориентирована, то

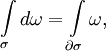
\int\limits_\sigma d\omega = \int\limits_{\partial \sigma} \omega,

где _d_ω обозначает внешний дифференциал формы ω.

Теорема распространяется на линейные комбинации подмногообразий одной размерности, так называемые цепи. В этом случае формула Стокса реализует двойственность между когомологией де Рама и гомологией циклов многообразия M.

Частные случаи

Формула Ньютона — Лейбница

Пусть дана кривая l, соединяющая две точки a и b (одномерная цепь) в многообразии произвольной размерности. Форма ω нулевой степени класса C1 — это дифференцируемая функция f. Формула Стокса тогда записывается в виде

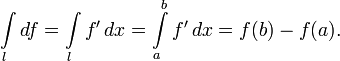
\int\limits_l df = \int\limits_l f'\,dx = \int\limits_a^b f'\,dx =f(b)-f(a).

Формула Грина

Пусть M — плоскость, а D — некоторая её ограниченная область с кусочно-гладкой жордановой границей. Форма первой степени, записанная в координатах x и y — это выражение 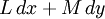L\,dx+M\,dy, и для интеграла этой формы по границе области D верно

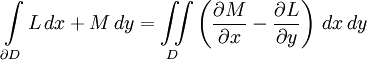
\int\limits_{\partial D} L\, dx + M\, dy = \iint\limits_{D} \left(\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y}\right)\, dx\,dy

Формула Кельвина — Стокса

Пусть Σ — кусочно-гладкая поверхность (p = 2) в трёхмерном евклидовом пространстве (n = 3), F — дифференцируемое векторное поле. Тогда циркуляция векторного поля вдоль замкнутого контура ∂Σ равна потоку ротора (вихря) поля через поверхность Σ, ограниченную контуром:

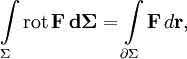
\int\limits_{\Sigma}\operatorname{rot}\, \mathbf{F} \, \mathbf{d\Sigma} = \int\limits_{\partial\Sigma} \mathbf{F}\, d \mathbf{r},

или в координатной записи

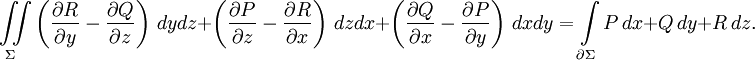
\iint\limits_{\Sigma}\left(\frac{\partial R}{\partial y}-\frac{\partial Q}{\partial z}\right)\,dydz+\left(\frac{\partial P}{\partial z}-\frac{\partial R}{\partial x}\right)\,dzdx+\left(\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right)\,dxdy=\int\limits_{\partial\Sigma}P\,dx+Q\,dy+R\,dz.

Формула Остроградского

Пусть теперь ∂V — кусочно-гладкая гиперповерхность (p = n−1), ограничивающая некоторую область V в n_-мерном пространстве. Тогда интеграл дивергенции поля по области равен потоку поля через границу области ∂_V:

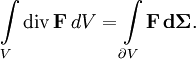
\int\limits_V \operatorname{div} \,\mathbf{F}\, dV=\int\limits_{\partial V} \mathbf{F} \, \mathbf{d\Sigma}.

Что эквивалентно записи:

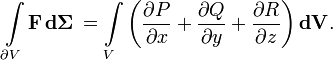
\int\limits_{\partial V} \mathbf{F} \, \mathbf{d\Sigma}\, =\int\limits_V \left(\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}+\frac{\partial R}{\partial z}\right)\mathbf{dV}.

Литература

См. также

Wikimedia Foundation.2010.

Полезное

Смотреть что такое "Формула Стокса" в других словарях: