SAFER | это... Что такое SAFER? (original) (raw)

SAFER
изображение
Создатель: Джеймс Мэсси
Создан: 1993 г.
Опубликован: 1993 г.
Размер ключа: 64 (128, 192, 256) бит
Размер блока: 64 (40, 128) бит
Число раундов: 6-16
Тип: Подстановочно-перестановочная сеть

SÁFER (англ. Secure And Fast Encryption Routine — безопасная и быстрая процедура шифрования) — в криптографии семейство симметричных блочных криптоалгоритмов на основе подстановочно-перестановочной сети. Основной вклад в разработку алгоритмов внёс Джеймс Мэсси. Первый вариант шифра был создан и опубликован в 1993 году.

Содержание

История

Существует несколько вариантов шифра, отличающихся друг от друга длиной ключа шифрования и размерами блоков исходного текста.

Первая разновидность алгоритма — SAFER K-64 была разработана Джэймсом Мэсси для калифорнийской корпорации «Cylinc» в 1993 году[1]. Опубликованный в том же году, алгоритм имел блок и ключ шифрования длиной в 64 бита. Для него рекомендовалось использовать 6 раундов шифрования. Однако, из-за необходимости увеличить длину ключа до 128 бит (так как была обнаружена слабость в первоначальном варианте алгоритма), Мэсси разработал новый вариант шифра SAFER K-128, который был опубликован на следующий год после SAFER K-64. Новый алгоритм включал в себя расписание ключей, разработанное министерством внутренних дел Сингапура, и в дальнейшем использовался им для различных целей. Также для этого алгоритма рекомендовалось использовать 10 (максимум 12) раундов шифрования.

Спустя некоторое время в первых вариантах алгоритма выявились некоторые слабости, обнаруженные Ларсом Кнудсеном и Шоном Мёрфи[1]. Это повлекло за собой создание новых версий алгоритма, названных SAFER SK-64 и SAFER SK-128, в которых расписание ключей было изменено в соответствии со схемой, предложенной Кнудсеном. Также был разработан вариант с длиной ключа, уменьшенной до 40 бит — SAFER SK-40. Сокращение «_SK_» в названии алгоритмов расшифровывается как «_Strengthened Key schedule_» (Усиленное расписание ключей). Для новых вариантов шифра предлагалось использовать не 6, а по крайней мере 8 (максимум 10) раундов шифрования.

Алгоритм SAFER+ был разработан в 1998 году калифорнийской корпорацией Cylinc совместно с Армянской академией наук для участия в конкурсе AES, на котором прошёл лишь первый отборочный тур. Данный шифр имеет входной блок длиной 128 бит и размер ключа 128, 192 или 256 бит.

Последней из созданных разновидностей алгоритма SAFER является SAFER++, разработанный Мэсси в 2000 году и ставший дальнейшим развитием алгоритма SAFER+. Алгоритм принял участие в европейском конкурсе алгоритмов NESSIE, где был представлен в двух вариантах: шифр с 64-битным блоком и 128-битным блоком. Он прошёл во вторую фазу конкурса, но не был выбран в набор рекомендуемых NESSIE криптографических примитивов. Эксперты сочли, что шифр слишком медленный на всех машинах, кроме 8-битных (таких как смарт-карты), а запас безопасности шифра слишком мал[2][3].

Алгоритмы SAFER не являются частной собственностью и не защищены авторскими правами, то есть могут быть использованы без каких либо ограничений. Поскольку они целиком состоят из простых байтовых операций (за исключением поворота байтов при генерации ключей), эти алгоритмы могут быть реализованы процессорами с малой разрядностью[4].

Ниже приведена сводная таблица всех существующих вариантов шифра SAFER

название англ. дата создания длина блока длина ключа число раундов
SAFER K-64 key 64 bit 1993 64 64 6
SAFER K-128 key 128 bit 1995 64 128 10 (максимум 12)
SAFER SK-64 Strengthened Key schedule, 64 bit 1995 64 64 8 (минимум 6, максимум 10)
SAFER SK-128 Strengthened Key schedule, 128 bit 1995 64 128 10 (максимум 12)
SAFER SK-40 Strengthened Key schedule, 40 bit 1995 64 40
SAFER+ SAFER Plus 1998 128 128, 192, 256 8, 12, 16
SAFER++ SAFER Plus Plus 2000 64, 128 128, 256 7, 10

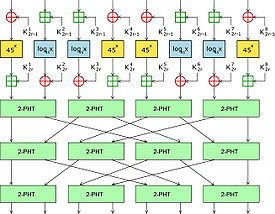
SAFER K-64

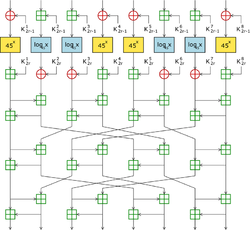
Алгоритм шифрования

схема действия одного раунда в алгоритмах SAFER K-64 и SAFER SK-64

Длина шифруемого блока и длина ключа равны 64 битам. Алгоритм является итеративным блочным шифром, то есть одна и та же функция шифрования последовательно применяется к входному блоку r раз, при этом на каждом этапе используются различные ключи. На каждой итерации (этапе, раунде) в рассматриваемом алгоритме берутся два 64-битных подключа.

Структура одного раунда алгоритма представлена на схеме. Опишем алгоритм поэтапно (ниже i пробегает значения от 1 до r, где r — число раундов шифрования):

  1. Входной блок B и оба ключа K{2i-1} и K{2i} разбиваются на 8 частей длиной по одному байту (8 бит). Соответствующие подблоки входного текста и ключа K{2i-1} либо складываются по модулю два (операция XOR) — для подблоков № 1, 4, 5 и 8, либо складываются по обычным правилам (операция сложения байтов по модулю 256) — для подблоков № 2, 3, 6 и 7.
  2. Результаты сложения проходят через так называемые S-блоки (S-boxes). Их содержимое представляет собой одну из нелинейных операций: y = 45^x\mbox{ mod }257 (где y = 0 когда x = 128) либо y = log_{45}x (y = 128 когда x = 0). Здесь x — входной байт, y — выходной байт. Данные операции являются операциями в конечном поле GF(257), где 45 — примитивный элемент поля. Поскольку каждый раз рассчитывать результаты этих операций в практических реализациях алгоритма весьма неудобно, как правило используются специально составляемые таблицы для получения результатов их действия.
  3. Над результатами предыдущего действия производится операция, аналогичная п.1, с той лишь разницей, что используется второй подключ K{2i}, а операции XOR и сложения по модулю 256 меняются местами.
  4. Полученные байты проходят через многоуровневую систему преобразований, взаимно складываясь в различном порядке. Это делается для достижения лучшего лавинного эффекта, то есть увеличения зависимости выходных битов от всех битов входного блока. На схеме преобразования представлены в виде сети операций сложения по модулю 256. Эта сеть эквивалентна трём уровням псевдопреобразований Адамара (Pseudo-Hadamard Transform, PHT)[5]. Каждое преобразование действует таким образом, что при входных байтах a_1 и a_2 на выходе получим:
    b_1 = (2a_1 + a_2) \mbox{ mod } 256
    b_2 = (a_1 + a_2) \mbox{ mod } 256

По завершении r последовательных раундов, над полученным результатом применяется операция, аналогичная п.1, где в качестве ключа используется последний подключ.

Автор алгоритма рекомендует использовать r=6 раундов, но можно увеличить их количество для увеличения надёжности[5].

Алгоритм расшифрования

Расшифрование производятся в обратном порядке, но при этом операции заменяются обратными. Так, операции сложения по модулю 256 заменяются операциями вычитания, а сложение по модулю 2 выполняется точно так же, как и при зашифровании. Операции 45^x\mbox{ mod }257 и log_{45}x меняются местами. Псевдопреобразования Адамара заменяются обратными (Inverse PHT, IPHT), действующими следующим образом:

a_1 = (b_1-b_2) \mbox{ mod } 256

a_2 = (-b_1+2b_2) \mbox{ mod } 256

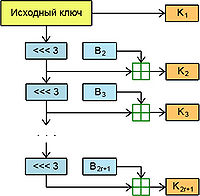
Генерация ключей

Первый ключ шифрования K_1 является секретным ключом, задаваемым пользователем. Каждый последующий ключ шифрования K_{i+1} получается из предыдущего K_i по формуле K_{i + 1} = \left( {K_1 <<< 3i} \right) + B_{i+1} (сложение производится по модулю 256, при этом байты складываются отдельно). Здесь операция «<<<3» — побайтовый циклический сдвиг влево на 3 бита, то есть сдвиг происходит внутри каждого отдельного байта ключа. Величина B_{i} называется константой этапа шифрования. Получить её можно следующим образом: если B_{ij} — _j_-й байт константы _i_-го этапа, то все константы этапов выражаются следующей формулой: B_{ij} = 45^{45^{((9i+j) \mbox{ mod } 256) }\mbox{ mod } 257} \mbox{ mod } 257[5]. Получаемые таким образом константы этапов с хорошей точностью ведут себя как случайные числа. Как правило, значения для всех этих констант хранят в специальных таблицах, чтобы уменьшить время на вычисления.

Алгоритм генерации ключей в SAFER K-64

Формальное описание алгоритма генерации ключей:[6]

ВХОД: 64-битовый ключ K=k_1,\dots,k_{64}; количество раундов r.

ВЫХОД: 64-битовые подключи K_1,\dots,K_{2r+1}. Байт K_i[j] — j-байт ключа K_i (нумерация слева направо).

  1. Пусть R[i] — 8-битовые величины. Пусть C_i[j] — _j_-й байт константы _i_-го этапа шифрования.
  2. (R[1],R[2],\dots,R[8])\leftarrow(k_1 \dots k_8, k_9 \dots k_{16}, k_{57} \dots k_{64}).
  3. (K_1[1],K_1[2],\dots,K_1[8]) \leftarrow (R[1],R[2],\dots,R[8]).
  4. Для i от 2 до 2r+1:

Криптоанализ алгоритма

Джэймс Мэсси доказал, что после шести раундов шифрования алгоритмом SAFER K-64 обеспечивается абсолютная устойчивость к дифференциальному криптоанализу[5]. При этом, уже после трёх раундов шифрования линейный криптоанализ также становится неэффективным для взлома[5].

Несмотря на это, в 1995 году Ларсом Кнудсеном была обнаружена слабость в алгоритме генерации ключей для SAFER K-64. Он показал[5], что для любого ключа шифрования K_{1} можно найти один или несколько (вплоть до девяти) ключей K_{2} (отличающихся от него значением лишь одного байта), таких, что при зашифровании двух различных исходных текстов M_{1} и M_{2} получается один и тот же шифротекст, что можно записать в виде E(M_1,K_1) = E(M_2,K_2). Число различных открытых текстов M, из которых получается один и тот же шифротекст, лежит в промежутке между 2^{22} и 2^{28} из возможных 2^{64} текстов. Таким образом, путём анализа от 2^{44} до 2^{47} открытых текстов можно вычислить 8 бит секретного ключа длиной 64-бита. Эта атака в дальнейшем была значительно усилена Джоном Келси, Брюсом Шнайером и Дэвидом Вагнером (англ.) (англ. David A. Wagner). Авторы атаки утверждали, что алгоритм легко поддаётся атакам на связанных ключах за счёт очень простой и однообразной процедуры генерации подключей[7].

Это свойство значительно уменьшает надёжность алгоритма SAFER K-64 при использовании его в качестве однонаправленной хэш-функции. Его надёжность как алгоритма шифрования при этом не уменьшается. Тем не менее, эта слабость алгоритма, вместе с атакой, в дальнейшем опубликованной Мёрфи, побудили Мэсси улучшить алгоритм генерации ключей. В результате в сентябре 1995 года им был опубликован алгоритм SAFER SK-64.

Ещё одна сертифицированная атака на алгоритм SAFER K-64 была осуществлена Ларсом Кнудсеном и Томасом Бёрсоном (англ.) (англ. Thomas A. Berson)[6]. Она была расcчитана на исходный текст длиной 2^{45}, зашифрованный 5 раундами алгоритма SAFER K-64. Хотя эта атака и не была способна взломать шифротекст уже при 6 раундах шифрования, она показала, что криптостойкость алгоритма меньше, чем изначально заявлял Мэсси (он утверждал, что алгоритм является абсолютно стойким к методам линейного криптоанализа).

Французский криптограф Серж Водено (англ.) (фр. Serge Vaudenay) показал, что при замене содержимого S-блоков случайными перестановками, алгоритм SAFER K-64 становится менее криптостойким[6].

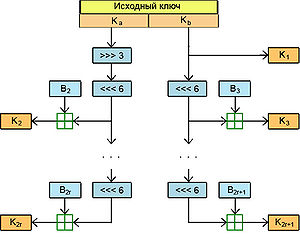
SAFER K-128

Алгоритм генерации ключей в SAFER K-128

Алгоритм отличается от SAFER K-64 только длиной пользовательского ключа и, соответственно, самим способом генерации ключей. Этот способ был разработан Министерством внутренних дел Сингапура[5] и впоследствии использован Джеймсом Мэсси в его алгоритме.

Генерация ключей

В этом алгоритме вместо одного ключа длиной 64 бита используется ключ длиной 128 бит, что эквивалентно заданию двух ключей длиной по 64 бита. Из этих двух ключей по методу, крайне схожему с использованным в шифре SAFER K-64, генерируются две независимые последовательности подключей. Ключи из этих последовательностей попеременно используются на всех раундах шифрования.

Как видно из схемы, на каждом этапе происходит побитовый сдвиг байтов ключа не на 3, а на 6 бит. Это приводит к тому, что, задавшись одинаковыми начальными ключами K_a = K_b, получим, что 128-битовый ключ совместим с 64-битовым ключом K_a. То есть, используя ключ вида K_aK_a в алгоритме SAFER K-128 и ключ K_a в SAFER K-64, получим одинаковые последовательности подключей, а значит и само шифрование в SAFER K-128 ничем не будет отличаться от такового в SAFER K-64.

Криптоанализ

При всей схожести алгоритма SAFER K-128 с его предшественником, существует и ряд отличий. Так, в новой версии алгоритма Джеймс Мэсси рекомендует использовать уже не 6, а 10 (максимум 12) раундов шифрования[7]. Это связано с тем, что при меньшем количестве итераций алгоритм, так же как и SAFER K-64, подвержен атаке, осуществлённой Ларсом Кнудсеном. Напомним, что она касается использования алгоритма в качестве основы для хэш-функции. Увеличение же количества раундов шифрования, по мнению автора, значительно повышает криптостойкость алгоритма в этом смысле[7].

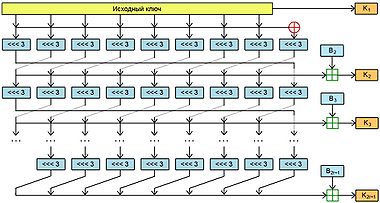
SAFER SK-64

Данный алгоритм отличается от SAFER K-64 лишь способом генерации подключей. Этот способ был предложен Ларсом Кнудсеном, после того как им же была найдена атака на алгоритм SAFER K-64. Рекомендуемое количество раундов шифрования увеличено по сравнению с изначальным вариантом с 6 до 8[7]. Различия в способах расширения ключа хорошо видны при формальном описании алгоритма:

Схема генерации подключей в SAFER SK-64

Формальное описание алгоритма генерации ключей:[6]

ВХОД: 64-битовый ключ K=k_1,\dots,k_{64}; количество раундов r.

ВЫХОД: 64-битовые подключи K_1,\dots,K_{2r+1}. Байт K_i[j] — j-байт ключа K_i (нумерация слева направо).

  1. Пусть R[i] — 8-битовые величины. Пусть B_i[j] — j-байт константы i-го этапа шифрования.
  2. (R[1],R[2],\dots,R[8]) \leftarrow (k_1 \dots k_8, k_9 \dots k_{16}, k_{57} \dots k_{64}); R[9] \leftarrow R[1]+R[2]+\dots+R[8] (сложение производится по модулю 2).
  3. (K_1[1],K_1[2],\dots,K_1[8]) \leftarrow (R[1],R[2],\dots,R[8])
  4. Для i от 2 до 2r+1:

Главной отличительной чертой этого алгоритма является использование дополнительного байта R[9], который получается из побитового сложения восьми байт ключа. Далее, на каждом этапе алгоритма происходит циклический сдвиг этих байт, в результате получается, что подключ K_1 зависит от байт R[1],R[2],\dots,R[8], подключ K_2 — от байт R[2],R[3],\dots,R[9], подключ K_3 — от байт R[3],\dots,R[9],R[1] и т. д. Побитовый сдвиг на 3 бита и структура констант шифрования остаются без изменений.

Криптоанализ

Такие, казалось бы, незначительные изменения в алгоритме генерации ключей, значительно повышают криптостойкость алгоритма. В настоящее время не известны атаки на алгоритмы SAFER SK-64 и SAFER SK-128 более эффективные, чем полный перебор ключей[7].

При этом существуют атаки, направленные на урезанные версии этих алгоритмов. Приведём некоторые из них:[7]

Как видно, все эти атаки не очень практичны, поскольку требуют достаточно больших ресурсов и времени.

SAFER SK-128

Данный алгоритм шифрования отличается от SAFER SK-64 точно таким же образом, каким SAFER K-128 отличается от SAFER K-64. А именно, сами алгоритмы шифрования и генерации подключей остаются прежними, но вместо одного исходного ключа длиной в 64 бита используется два таких ключа, для каждого из которых независимо формируются последовательности подключей, которые затем применяются поочерёдно. При этом каждая последовательность для чётных и для нечётных ключей аналогична по структуре алгоритму расширения ключа в SAFER SK-64. В ней точно так же на первом этапе вводится дополнительный байт, являющийся суммой по модулю 2 остальных восьми байт, и затем на каждом этапе происходит побайтовый циклический сдвиг.

Стоит отметить, что, как и для алгоритмов SAFER K-64 и SAFER K-128, при использовании пользовательского ключа вида K_aK_a в SAFER SK-128 и ключа K_a в SAFER SK-64, действие алгоритмов оказывается совершенно одинаковым. При этом количество раундов шифрования, рекомендуемое для SAFER SK-128, остаётся таким же, как и в SAFER K-128, и равно 10[7].

SAFER SK-40

Данный вариант шифра использует уменьшенный ключ длиной всего 40 бит (5 байт). Это позволяло алгоритму обойти экспортные ограничения, существовавшие на тот момент в США. Алгоритм работает практически таким же образом, как и SAFER SK-64, с одним небольшим отличием на начальном этапе генерации подключей.

В алгоритме SAFER SK-64 к 8 байтам исходного ключа приписывался девятый байт, равный их побитовой сумме по модулю 2. В SAFER SK-40 эти 9 байт получаются совершенно иначе. Обозначим их KI_1, KI_2, … KI_9. Первые 5 из них — это байты исходного ключа. Остальные 4 байта получаются из первых следующим образом[11]:

KI_6 = KI_1 \oplus KI_3 \oplus 129,

KI_7 = KI_1 \oplus KI_4 \oplus KI_5 \oplus 66,

KI_8 = KI_2 \oplus KI_3 \oplus KI_5 \oplus 36,

KI_9 = KI_2 \oplus KI_4 \oplus 24;

Первый подключ K_1 получается из первых восьми полученных байт. Последующие подключи генерируются с их использованием точно таким же образом, как и в алгоритме SAFER SK-64.

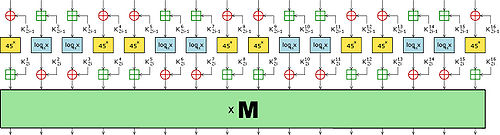
SAFER+

один раунд алгоритма SAFER+

SAFER+ представляет собой улучшенный вариант алгоритмов семейства SAFER. Алгоритм разработан в 1998 году для участия в конкурсе на стандарт AES. Над его созданием совместно трудились специалисты из калифорнийской корпорации Cylinc (Джеймс Мэсси) и Академии наук республики Армении (Гурген Хачатрян и Мельсик Курегян)[2].

В конкурсе AES алгоритм прошёл первый отборочный тур наряду с 14 другими алгоритмами. В финал конкурса, к которому допускались лишь 5 алгоритмов, SAFER+ не прошёл, поскольку по результатам тщательного анализа оказалось, что он подвержен ряду атак и имеет низкую скорость выполнения[12]. Алгоритм создавался для работы на 8-битных процессорах, и как следствие, достаточно медленно работает на 32-битных процессорах[3].

SAFER+ обрабатывает данные 128-битным блоком. Алгоритм поддерживает 128, 192 и 256-битные ключи в соответствии с требованиями, предъявленными Национальным институтом стандартов и технологий США (NIST)[13]. Количество раундов шифрования зависит от размера ключа:

Алгоритм шифрования

По структуре алгоритм SAFER+ напоминает SAFER K-64. Он состоит из тех же основных этапов, несколько отличающихся по своей структуре. На каждом раунде работы алгоритма сначала происходит подмешивание одного подключа, после этого байты проходят через блоки нелинейной замены, затем подмешивается второй подключ и происходит линейное перемешивание байт. Подключи последовательно генерируются с использованием входного ключа. Ниже приведено более подробное описание работы одной итерации (i — номер итерации):

  1. Наложение ключа K_{2i-1}: байты входного блока складываются с байтами ключа K_{2i-1}, причём используется сложение по модулю 2 для байт с номерами 1, 4, 5, 8, 9, 12, 13 и 16, и сложение по модулю 256 для байт с номерами 2, 3, 6, 7, 10, 11, 14 и 15.
  2. Нелинейное преобразование: к байтам с номерами 1, 4, 5, 8, 9, 12, 13 и 16 применяется операция 45^x(mod 257) (причём 45^{128}(mod 257)=256 заменяется нулём). К байтам с номерами 2, 3, 6, 7, 10, 11, 14 и 15 применяется операция log_{45}(x) (причём log_{45}(0)=128). результаты действия этих операций как и для других разновидностей алгоритма SAFER на практике часто хранят в специальных таблицах. В данном случае для этого требуется 512 байт.
  3. Наложение ключа K_{2i}: байты входного блока складываются с байтами ключа K_{2i}, но в отличие от п.1 операции сложения по модулю 2 и по модулю 256 меняются местами.
  4. Линейное преобразование: умножение 16-байтного блока данных справа на специальную невырожденную матрицу M (все операции при этом байтовые и производятся по модулю 256). Умножение на эту матрицу эквивалентно четырём уровням преобразования PHT, между которыми выполняются некоторые байтовые перестановки[2]. Стоит отметить, что эта часть алгоритма является наиболее громоздкой с вычислительной точки зрения.

После проведения r раундов шифрования производится подмешивание ключа K_{2r+1}, аналогичное подмешиванию ключей K_{2i-1}.

Алгоритм расшифрования

Операции в алгоритме расшифрования подобны операциям шифрования и производятся в обратном порядке. Разница состоит в следующем:

  1. Вместо матрицы M умножение происходит с обратной ей матрицей M^{-1};
  2. Все операции сложения по модулю 256 заменяются операциями вычитания;
  3. Операции 45^x\mbox{ (mod } 257) и log_{45} x (являющиеся обратными друг другу) меняются местами.

При шифровании используется следующая матрица M:[13]

2 2 1 1 16 8 2 1 4 2 4 2 1 1 4 4
1 1 1 1 8 4 2 1 2 1 4 2 1 1 2 2
1 1 4 4 2 1 4 2 4 2 16 8 2 2 1 1
1 1 2 2 2 1 2 1 4 2 8 4 1 1 1 1
4 4 2 1 4 2 4 2 16 8 1 1 1 1 2 2
2 2 2 1 2 1 4 2 8 4 1 1 1 1 1 1
1 1 4 2 4 2 16 8 2 1 2 2 4 4 1 1
1 1 2 1 4 2 8 4 2 1 1 1 2 2 1 1
2 1 16 8 1 1 2 2 1 1 4 4 4 2 4 2
2 1 8 4 1 1 1 1 1 1 2 2 4 2 2 1
4 2 4 2 4 4 1 1 2 2 1 1 16 8 2 1
2 1 4 2 2 2 1 1 1 1 1 1 8 4 2 1
4 2 2 2 1 1 4 4 1 1 4 2 2 1 16 8
4 2 1 1 1 1 2 2 1 1 2 1 2 1 8 4
16 8 1 1 2 2 1 1 4 4 2 1 4 2 4 2
8 4 1 1 1 1 1 1 2 2 2 1 2 1 4 2

При расшифровании используется обратная матрица M^{-1}:[13]

2 −2 1 −2 1 −1 4 −8 2 −4 1 −1 1 −2 1 −1
−4 4 −2 4 −2 2 −8 16 −2 4 −1 1 −1 2 −1 1
1 −2 1 −1 2 −4 1 −1 1 −1 1 −2 2 −2 4 −8
−2 4 −2 2 −2 4 −1 1 −1 1 −1 2 −4 4 −8 16
1 −1 2 −4 1 −1 1 −2 1 −2 1 −1 4 −8 2 −2
−1 1 −2 4 −1 1 −1 2 −2 4 −2 2 −8 16 −4 4
2 −4 1 −1 1 −2 1 −1 2 −2 4 −8 1 −1 1 −2
−2 4 −1 1 −1 2 −1 1 −4 4 −8 16 −2 2 −2 4
1 −1 1 −2 1 −1 2 −4 4 −8 2 −2 1 −2 1 −1
−1 1 −1 2 −1 1 −2 4 −8 16 −4 4 −2 4 −2 2
1 −2 1 −1 4 −8 2 −2 1 −1 1 −2 1 −1 2 −4
−1 2 −1 1 −8 16 −4 4 −2 2 −2 4 −1 1 −2 4
4 −8 2 −2 1 −2 1 −1 1 −2 1 −1 2 −4 1 −1
−8 16 −4 4 −2 4 −2 2 −1 2 −1 1 −2 4 −1 1
1 −1 4 −8 2 −2 1 −2 1 −1 2 −4 1 −1 1 −2
−2 2 −8 16 −4 4 −2 4 −1 1 −2 4 −1 1 −1 2

Генерация ключей

Излагаемый алгоритм применим для входных ключей длиной в 128, 192 и 256 бит (16, 24 и 32 байт соответственно). Первый подключ K_1 представляет собой первые 16 байт входного ключа. Генерация остальных ключей производится следующим образом: сначала исходный ключ целиком записывается в ключевой регистр длиной на 1 байт длиннее самого ключа (то есть длина регистра равна для разных входных ключей 17, 25 или 33 байтам). Все байты ключа суммируются по модулю 2 поразрядно, результат записывается в последний байт регистра. Для получения каждого следующего ключа над содержимым регистра выполняются следующие операции (для i от 2 до 2_r_+1):

  1. Содержимое байт ключевого регистра циклически сдвигается влево на 3 позиции (сдвиг происходит внутри байт в отдельности, а не регистра как целого);
  2. Из регистра выбираются 16 байт. При этом для ключа K_i выбираются байты регистра начиная с _i_-го и далее по циклу.
  3. Отобранные 16 байт складываются по модулю 256 с байтами слова смещения B_i (смотри ниже). Результат сложения и будет являться подключом K_i.

Слова смещения B_i — это 16-байтные константы, вычисляемые по следующей формуле: B_{i,j} = \begin{cases} 45^{45^{17i+j}\mbox{ mod }257}\mbox{ mod }257, & i\mbox{ = 2,3,... 17; }j \mbox{ = 1,3,... 16} \\ 45^{17i+j}\mbox{ mod }257, & i\mbox{ = 18,19,... 33; }j \mbox{ = 1,3,... 16} \end{cases}

B_{i,j} — _j_-й байт _i_-го слова смещения. Если B_{i,j}=256 то этот байт заменяется на 0.

Понятно, что поскольку для различных длин ключей количество итераций шифрования различно (и равно 8, 12 и 16 для ключей длиной 128, 192 и 256 бит соответственно), то и использованы будут не все блоки смещения. Так, при длине ключа в 128 бит будут использованы только B_2, … B_{17}, для ключа в 192 бита — B_2, … B_{25}, а для ключа в 256 бит — все слова смещения.

Криптоанализ

В связи с участием алгоритма SAFER+ в конкурсе AES, к его криптоанализу было обращено весьма пристальное внимание криптологов. В результате было найдено несколько атак на алгоритм. Перечислим некоторые из них:

В ходе конкурса AES алгоритм SAFER+ был охарактеризован следующим образом:[2]

SAFER++

Алгоритм является дальнейшим развитием SAFER+, и практически полностью наследует его структуру. Различия заключаются в основном в оптимизации (с точки зрения облегчения вычислений) некоторых участков алгоритма. Он использует меньшее число раундов: семь для 128-битного ключа и десять для 256-битного ключа. Длина блока в этом шифре равна 128 битам, но помимо этого предусматривается режим «обратной совместимости» при использовании блоков длиной 64 бита.

Алгоритм прошёл во вторую фазу конкурса NESSIE, но не был выбран в набор рекомендуемых NESSIE криптографических примитивов. Эксперты сочли, что шифр слишком медленный на всех машинах, кроме смарт-карт, а запас безопасности шифра слишком мал[17].

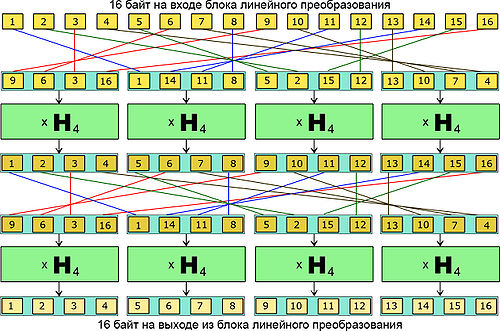
Алгоритм

структура блока линейного преобразования алгоритма SAFER++

Значительная часть процедуры шифрования ничем не отличается от таковой в алгоритме SAFER+. Главное различие заключается в процедуре линейного преобразования, которая была значительно оптимизирована с вычислительной точки зрения (в SAFER+ необходимо производить перемножение с матрицей размеров 16x16, что требует большого количества операций побайтового сложения).

Линейное преобразование, как видно из схемы, состоит из следующих этапов:

  1. 16 входных байтов перемешиваются в следующем порядке: [9, 6, 3, 16, 1, 14, 11, 8, 5, 2, 15, 12, 13, 10, 7, 4];
  2. Байты в новом порядке разбиваются на группы по 4. Каждая группа подвергается 4-точечному псевдопреобразованию Адамара;
  3. После преобразования байты вновь перемешиваются в том же порядке, что и в п.1;
  4. Аналогично п.2 байты снова проходят через псевдопреобразования Адамара. Результат подаётся на выход.

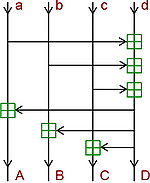
Псевдопреобразование Адамара заключается в умножении 4-байтовой строки на невырожденную матрицу 4x4, которая имеет следующую структуру:

H_4= \begin{bmatrix} 2 & 1 &1 &1\\ 1 & 2 &1 &1\\ 1 & 1 &2 &1\\ 1 & 1 &1 &1 \end{bmatrix} .

Обратная матрица, используемая при расшифровании, имеет вид

H^{-1}_4= \begin{bmatrix} 1 & 0 &0 &-1\\ 0 & 1 &0 &-1\\ 0 & 0 &1 &-1\\ -1 & -1 &-1 &4 \end{bmatrix}

Преимущество такого подхода по сравнению с умножением на матрицу 16x16, используемую в SAFER+, состоит в том, что для линейного преобразования, в силу структуры матриц преобразования Адамара, требуется значительно меньшее количество элементарных операций. А именно, при умножении 16-байтовой строки на матрицу 16x16 в общем случае требуется 15*16 операций сложения и 16*16 операций умножения. Умножение же на матрицу Адамарова преобразования требует всего лишь 6 операций сложения:[13]

схематическое представление умножения на матрицу 4-точечного псевдопреобразования Адамара

Если a, b, c, d — входные байты, A, B, C, D — выходные байты, то вычисления представимы формулами (сложение производится по модулю 256):

D=a+b+c+d (3 операции сложения),

A=D+a (1 операция сложения),

B=D+b (1 операция сложения),

C=D+c (1 операция сложения).

Таким образом, даже принимая во внимание, что умножение на матрицу H_4 производится 8 раз, получаем всего 6*8=48 операций, что значительно меньше, чем в SAFER+ (даже с учётом всех производимых байтовых перестановок в алгоритме SAFER++).

Всю структуру линейного преобразования можно, так же, как и в SAFER+, представить в виде невырожденной матрицы 16x16. Однако, большинство элементов в этой матрице будет равно единице. В обратной матрице, необходимой для совершения процедуры расшифрования, большинство элементов будет равно нулю.

Генерация ключей

Существуют также некоторые отличия от SAFER+ в алгоритме генерации подключей, используемых на различных раундах шифрования. В этом плане различия между SAFER+ и SAFER++ подобны различиям между SAFER K-64 и SAFER K-128, в том смысле, что в SAFER++ чётные и нечётные подключи генерируются независимо друг от друга. Рассмотрим алгоритм более детально.

Используются 2 ключевых регистра длиной 16+1=17 байт. В случае, если длина пользовательского ключа равна 128 битам (16 байт), в оба регистра изначально записывается этот ключ. Если же длина ключа равна 256 битам (32 байта), в первый регистр вписываются байты ключа с 1-го по 16-й, а во второй — с 17-го по 32-ой. На место 17-го байта в каждый регистр вписывается байтовая контрольная сумма от первых 16-и байт. После этого для i от 1 до 2r+1 (r — количество раундов шифрования) производятся следующие действия (для i = 1,3, … 2_r_+1 рассматривается первый регистр, для i = 2,4, … 2_r_ — второй регистр):

  1. Выбираются 16 байт из регистра, начиная с номера i и далее по циклу. Так, для ключа с номером _i_=5 байты будут выбраны следующим образом: [5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 1, 2, 3],
  2. Полученные байты складываются с соответствующим словом смещения B_i (смотри ниже)
  3. Содержимое всех байт регистра циклически сдвигается на 6 бит в случае нечётного i, и на 3 бита в случае чётного i.

Слова смещения вычисляются практически так же, как и в SAFER+, с той лишь разницей, что изменяются диапазоны изменения параметра i: B_{i,j} = \begin{cases} 45^{45^{17i+j}\mbox{ mod }257}\mbox{ mod }257, & i\mbox{ = 2,3,... 15; } j\mbox{ = 1,2,... 16} \\ 45^{17i+j}\mbox{ mod }257, & i\mbox{ = 16,17,... 21; } j\mbox{ = 1,2,... 16} \end{cases}

Криптоанализ

В рамках конкурса NESSIE алгоритм SAFER++ был тщательно исследован на криптостойкость. По заключению экспертов уязвимости предшествующего ему алгоритма SAFER+ не были унаследованы. Для полнораундового алгоритма SAFER++ не было найдено никаких новых атак. При этом был осуществлён ряд атак на варианты шифра с уменьшенным числом раундов шифрования[9][18][19] Одна из них, будучи неосуществимой вследствие огромного числа необходимых вычислений, теоретически способна взломать SAFER++ с 5,5 раундами вместо семи.[20]. Эта атака послужила одной из основных причин, по которым алгоритм не победил в конкурсе. Также, по мнению некоторых экспертов, алгоритм вполне может содержать невыявленные на настоящий момент слабости. Основной же причиной явилось недостаточное быстродействие алгоритма при реализации на многоразрядных устройствах.

Практическое использование

Хотя алгоритмы SAFER не получили статуса стандартов в США или ЕС, они нашли весьма широкое применение. В частности, SAFER+ используется в качестве основы протокола аутентификации в Bluetooth. Однако, в самом алгоритме шифрования в Bluetooth этот алгоритм не используется[1].

Несмотря на то, что в названии алгоритма фигурирует слово «_fast_» (быстрый), по современным меркам алгоритмы семейства SAFER являются достаточно медленными.

С точки зрения криптостойкости даже самая первая версия алгоритма SAFER K-64 является абсолютно устойчивой к дифференциальному криптоанализу. Последний алгоритм семейства — SAFER++, будучи значительно модифицированным с учетом множества атак, осуществленных на более ранние версии алгоритма, стал ещё более устойчивым. В настоящее время никаких реально осуществимых атак на алгоритм не найдено[1].

Учитывая, насколько далеко продвинулись алгоритмы SAFER за время своего существования — от SAFER K-64 до SAFER++, можно предположить, что на этом развитие этих алгоритмов не закончено[2].

Интересные факты

Как известно, аббревиатура «_SK_» в алгоритмах SAFER SK-64/128/40 расшифровывается как Strengthened Key Schedule, что означает «Усиленное расширение ключа». Однако, существует известная шутка, что на самом деле «_SK_» означает «_Stop Knudsen_» (Остановить Кнудсена), объясняющаяся тем, что новая процедура генерации ключей делает атаку Кнудсена безуспешной. Стоит отметить, что эта процедура была разработана самим Ларсом Кнудсеном[21].

Примечания

  1. ↑ 1 2 3 4 Swarnendu Mukherjee, Debashis Ganguly, Somnath Naskar A New Generation Cryptographic Technique // International Journal of Computer Theory and Engineering, Vol. 1, No. 3. — Август 2009. — С. 284-287.
  2. ↑ 1 2 3 4 5 Панасенко С.П. Эволюция алгоритмов шифрования, шифры SAFER+ и SAFER++ (рус.) (12 июля 2007). — Статья с подробным рассмотрением алгоритмов SAFER+ и SAFER++. Проверено 12 ноября 2009.
  3. ↑ 1 2 Б. Киви Конкурс на новый криптостандарт AES (рус.) (апрель 1999). — Краткое описание алгоритма SAFER+. Архивировано из первоисточника 1 февраля 2012. Проверено 12 ноября 2009.
  4. ↑ James L. Massey SAFER K-64: A Byte.Oriented Block-Ciphering Algorithm // Fast Software Encryption. — 1993. — С. 1-17.
  5. ↑ 1 2 3 4 5 6 7 Шнайер Б. Глава 14. И ещё блочные шифры // Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си = Applied Cryptography. Protocols, Algorithms and Source Code in C. — М.: Триумф, 2002. — С. 382—384. — 816 с. — 3000 экз. — ISBN 5-89392-055-4
  6. ↑ 1 2 3 4 A. Menezes, P. van Oorschot, S. Vanstone. Handbook of Applied Cryptography. — CRC-Press, 1996. — 816 p. — (Discrete Mathematics and Its Applications). — ISBN 0-8493-8523-7
  7. ↑ 1 2 3 4 5 6 7 Панасенко С.П. Эволюция алгоритмов шифрования, алгоритмы SAFER K и SAFER SK (рус.) (15 июня 2007). — Статья с подробным рассмотрением алгоритмов SAFER K-64/128 и SAFER SK-64/128. Проверено 12 ноября 2009.
  8. ↑ Панасенко С.П. Современные методы вскрытия алгоритмов шифрования, часть 5 (рус.) (25 декабря 2006). — Описание метода невозможных дифференциалов. Проверено 12 ноября 2009.
  9. ↑ 1 2 3 4 Nakahara J.Jr., Preneel B., Vandewalle J. Impossible Differential Attacks on Reduced-Round SAFER Ciphers // Katholieke Universiteit Leuven, Belgium. — 12 марта, 2003.
  10. ↑ 1 2 Nakahara J.Jr. Cryptanalysis and Design of Block Ciphers // Katholieke Universiteit Leuven. — Июнь, 2003.
  11. ↑ Savard, John SAFER (Secure And Fast Encryption Routine) (англ.). — описание алгоритмов SAFER K и SAFER SK. Архивировано из первоисточника 31 января 2012. Проверено 22 декабря 2009.
  12. ↑ Панасенко С.П. Алгоритмы шифрования — финалисты конкурса AES (рус.) (24 августа 2006 г.). — содержатся выводы о характеристиках алгоритма SAFER+. Архивировано из первоисточника 31 января 2012. Проверено 12 ноября 2009.
  13. ↑ 1 2 3 4 С.Баричев, Р.Серов Основы современной криптографии. — V 1.2.. — Москва, 2001. — С. 36-41. — 122 с.
  14. ↑ 1 2 J. Kelsey, B. Schneier, and D. Wagner Key Schedule Weakness in SAFER+ (англ.) // Second AES Candidate Conference. — 1999.
  15. ↑ Eli Biham, Adi Shamir Power Analysis of the Key Scheduling of the AES Candidates (англ.) // Second AES Candidate Conference. — 1999.
  16. ↑ S. Chari, C. Jutla, J.R. Rao, P. Rohatgi A Cautionary Note Regarding Evaluation of AES Candidates on Smart-Cards (англ.) // Second AES Candidate Conference. — 1999.
  17. ↑ New European Schemes for Signatures, Integrity, and Encryption // v. 0.15. — Final report of European project IST-1999-12324, 19 апреля, 2004 г.. — С. 476.
  18. ↑ Nakahara J.Jr. An Update to Linear Cryptanalysis of SAFER++ (англ.) // Katholieke Universiteit Leuven, Belgium. — 12 марта, 2003.
  19. ↑ Piret G., Quisquater J.-J. Integral Cryptanalysis on reduced-round SAFER++ (англ.) // Universite catolique de Louvain, Louvain-la-Neuve, Belgium.
  20. ↑ Biryukov A., De Canniere C., Dellkrantz G. Cryptanalysis of SAFER++ (англ.) // K.U.Leuven, Belgium. — 2003.
  21. ↑ RSA FAQ (англ.). Архивировано из первоисточника 31 января 2012. Проверено 19 ноября 2009.

Литература

Ссылки

На русском языке

На других языках

Просмотр этого шаблона Симметричные криптосистемы
Поточный шифр A3 • A5 • A8 • Decim • MICKEY • RC4 • Rabbit • SEAL • SOSEMANUK • Trivium • VMPC
Сеть Фейстеля ГОСТ 28147-89 • Blowfish • Camellia • CAST-128 • CAST-256 • CIPHERUNICORN-A • CIPHERUNICORN-E • CLEFIA • Cobra • DFC • DEAL • DES • DESX • EnRUPT • FEAL • FNAm2 • HPC • IDEA • KASUMI • Khufu • LOKI97 • MARS • NewDES • Raiden • RC5 • RC6 • RTEA • SEED • Sinople • TEA • Triple DES • Twofish • XTEA • XXTEA
SP-сеть 3-WAY • ABC • AES (Rijndael) • Akelarre • Anubis • ARIA • BaseKing • BassOmatic • CRYPTON • Diamond2 • Grand Cru • Hierocrypt-L1 • Hierocrypt-3 • KHAZAD • Lucifer • Present • Rainbow • SAFER • Serpent • SHARK • SQUARE • Threefish
Другие FROG • NUSH • REDOC • SHACAL • SC2000

Эта статья входит в число хороших статей