Даламбер | это... Что такое Даламбер? (original) (raw)
Латур. Жан Лерон Даламбер.
Жан Леро́н Д’Аламбе́р (д’Аламбер, Даламбер; фр. Jean Le Rond d'Alembert, D'Alembert; 16 ноября 1717 — 29 октября 1783) — французский учёный-энциклопедист. Широко известен как философ, математик и механик. Член Парижской академии наук (1740), Французской Академии (1754), Петербургской (1764) и других академий.
Содержание
Биография
Даламбер был незаконным сыном маркизы де Тансен[1] от артиллерийского офицера Детуша. Вскоре после рождения младенец был подкинут матерью на ступени парижской церкви Св. Иоанна Круглого (фр. Jean le Rond). В честь этого святого ребёнок был назван Жаном Лероном. Воспитывался в усыновившей его семье стекольщика Руссо.
Отец в это время был за границей. Вернувшись во Францию, Детуш привязался к сыну, часто навещал его, помогал приёмным родителям и оплатил образование Даламбера, хотя официально признать не решился. Мать-маркиза никакого интереса к сыну так и не проявила. Позднее, став знаменитым, Даламбер никогда не забывал стекольщика и его жену, помогал им материально и всегда с гордостью называл своими родителями.
Фамилия д’Аламбер, по одним сведениям, произведена из имени его приёмного отца Аламбера, по другим — придумана самим мальчиком или его опекунами: сначала Жан Лерон был записан в школе как Дарамбер (Daremberg), потом сменил это имя на D’Alembert.
1726: Детуш, уже ставший генералом, неожиданно умирает. По завещанию Даламбер получает пособие в 1200 ливров в год и препоручается вниманию родственников. Мальчик воспитывается наряду с двоюродными братьями и сёстрами, но живёт по-прежнему в семье стекольщика. Он жил в доме приёмных родителей до 1765 года, то есть до 48-летнего возраста [2].
Рано проявившийся талант позволил мальчику получить хорошее образование — сначала в коллегии Мазарини (получил степень магистра свободных наук), затем в Академии юридических наук, где он получил звание лиценциата прав. Однако профессия адвоката ему была не по душе, и он стал изучать математику.
Уже в возрасте 22 лет Даламбер представил Парижской академии свои сочинения, а в 23 года был избран адъюнктом Академии.
«Трактат о динамике» Даламбера
1743: вышел «_Трактат о динамике_», где сформулирован фундаментальный «Принцип Д’Аламбера», сводящий динамику несвободной системы к статике. Здесь он впервые сформулировал общие правила составления дифференциальных уравнений движения любых материальных систем.
Позже этот принцип был применен им в трактате «Рассуждения об общей причине ветров» (1774) для обоснования гидродинамики, где он доказал существование наряду с океанскими также воздушных приливов.
1748: блестящее исследование задачи о колебаниях струны.
С 1751 года Д’Аламбер работал вместе с Дидро над созданием знаменитой «_Энциклопедии наук, искусств и ремёсел_». Статьи 17-томной «Энциклопедии», относящиеся к математике и физике, написаны Даламбером. В 1757 году, не выдержав преследований реакции, которым подвергалась его деятельность в «Энциклопедии», он отошёл от её издания и целиком посвятил себя научной работе (хотя статьи для «Энциклопедии» продолжал писать). «Энциклопедия» сыграла большую роль в распространении идей Просвещения и идеологической подготовке Французской революции.
1754: Даламбер становится членом Французской Академии.
1764: в статье «Размерность» (для Энциклопедии) впервые высказана мысль о возможности рассматривать время как четвёртое измерение.
Статуя Даламбера в Лувре
Даламбер вёл активную переписку с российской императрицей Екатериной II [3]. В середине 1760-х годов Даламбер был приглашён ею в Россию, в качестве воспитателя наследника престола, однако приглашения не принял.
1772: Даламбер избран непременным секретарём Французской Академии.
1783: после долгой болезни Даламбер умирает. Церковь отказывает «отъявленному атеисту» в месте на кладбище, и его похоронили в общей могиле, ничем не обозначенной.
Научные достижения
Математика
В первых томах знаменитой «Энциклопедии» Д’Аламбер поместил важные статьи: «Дифференциалы», «Уравнения», «Динамика» и «Геометрия», в которых подробно излагал свою точку зрения на актуальные проблемы науки.
Исчисление бесконечно малых Д’Аламбер стремился обосновать с помощью теории пределов, близкой к ньютоновскому пониманию «метафизики анализа». Он назвал одну величину пределом другой, если вторая, приближаясь к первой, отличается от нее менее чем на любую заданную величину. «_Дифференцирование уравнений состоит попросту в том, что находят пределы отношения конечных разностей двух переменных, входящих в уравнение_» — эта фраза могла бы стоять и в современном учебнике. Он исключил из анализа понятие актуальной бесконечно малой, допуская его лишь для краткости речи.
Перспективность его подхода несколько снижалась тем, что стремление к пределу он почему-то понимал как монотонное (видимо, чтобы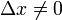 
), да и внятной теории пределов Даламбер не дал, ограничившись теоремами о единственности предела и о пределе произведения. Большинство математиков (в т. ч. Лазар Карно) возражали против теории пределов, так как она, по их мнению, устанавливала излишние ограничения — рассматривала бесконечно малые не сами по себе, а всегда в отношении одной к другой, и нельзя было в стиле Лейбница свободно использовать алгебру дифференциалов. И всё же подход Даламбера к обоснованию анализа в конце концов одержал верх, правда, только в XIX веке.
В теории рядов его имя носит широко употребительный достаточный признак сходимости.
Основные математические исследования Д’Аламбера относятся к теории дифференциальных уравнений, где он дал метод решения дифференциального уравнения 2-го порядка в частных производных, описывающего поперечные колебания струны (волнового уравнения). Даламбер представил решение как сумму двух произвольных функций, и по т. н. граничным условиям сумел выразить одну из них через другую. Эти работы Д’Аламбера, а также последующие работы Л. Эйлера и Д. Бернулли составили основу математической физики.
В 1752 году, при решении одного дифференциального уравнения с частными производными эллиптического типа (модель обтекания тела), встретившегося в гидродинамике, Д’Аламбер впервые применил функции комплексного переменного. У Д’Аламбера (а вместе с тем и у Л. Эйлера) встречаются те уравнения, связывающие действительную и мнимую части аналитической функции, которые впоследствии получили название условия Коши — Римана, хотя по справедливости их следовало бы назвать условиями Даламбера-Эйлера. Позже те же методы применялись в теории потенциала. С этого момента начинается широкое и плодотворное использование комплексных величин в гидродинамике.
Д’Аламберу принадлежат также важные результаты в теории обыкновенных дифференциальных уравнений с постоянными коэффициентами и систем таких уравнений 1-го и 2-го порядков.
Д’Аламбер дал первое (не вполне строгое) доказательство основной теоремы алгебры. Во Франции она называется теоремой Даламбера-Гаусса.
Физика, механика и другие работы
Выше уже упоминался открытый им принцип Д’Аламбера, указавший, как строить математическую модель движения несвободных систем.
Выдающийся вклад Д’Аламбер внёс также в небесную механику. Он обосновал теорию возмущения планет и первым строго объяснил теорию предварения равноденствий и нутации.
Опираясь на систему Фрэнсиса Бэкона, Д’Аламбер классифицировал науки, положив начало современному понятию «гуманитарные науки».
Д’Аламберу принадлежат также работы по вопросам музыкальной теории и музыкальной эстетики: трактат «О свободе музыки», в котором подведены итоги т. н. войны буффонов — борьбы вокруг вопросов оперного искусства, и др.
Философия
Из философских работ наиболее важное значение имеют вступительная статья к «Энциклопедии», «Очерк происхождения и развития наук» (1751, рус. пер. в книге «Родоначальники позитивизма», 1910), в которой дана классификация наук, и «Элементы философии» (1759).
В теории познания вслед за Дж. Локком Д’Аламбер придерживался сенсуализма. В решении основных философских вопросов Д’Аламбер склонялся к скептицизму, считая невозможным что-либо достоверно утверждать о Боге, взаимодействии его с материей, вечности или сотворённости материи и т. п. Сомневаясь в существовании Бога и выступая с антиклерикальной критикой, Д’Аламбер, однако, не встал на позиции атеизма.
В отличие от французских материалистов, Д’Аламбер считал, что существуют неизменные, не зависящие от общественной среды нравственные принципы. Взгляды Д’Аламбера по вопросам теории познания и религии были подвергнуты критике со стороны Дидро в произведении: «Сон Д’Аламбера» (1769), «Разговор Д’Аламбера и Дидро» (1769) и др.
Цитаты
- Работайте, работайте — а понимание придёт потом.
- Я не могу считать законным трату своих избытков, пока другие люди лишены необходимого…
Примечания
- ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. III. — С. 71.
- ↑ Стиллвелл Д. Математика и ее история. — Москва-Ижевск: Институт компьютерных исследований, 2004, стр. 270.
- ↑ Избранная переписка Даламбера и Екатерины II.
См. также
Литература
История математики под редакцией А. П. Юшкевича, в 3 т. — М.: Наука.
Избранная переписка Даламбера и Екатерины II. // Исторический вестник. № 4, 1884.
История в энциклопедии Дидро и Д’Аламбера. Серия «Памятники исторической мысли». — Л: Наука, Ленинградское отделение, 1978.
Джон Дж. О’Коннор и Эдмунд Ф. Робертсон. Д’Аламбер, Жан Лерон в архиве MacTutor
English translation of part of the Encyclopédie of Diderot and d’Alembert
Ссылки
Wikimedia Foundation.2010.