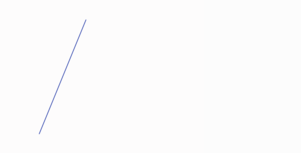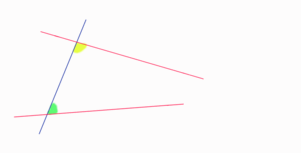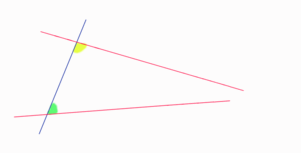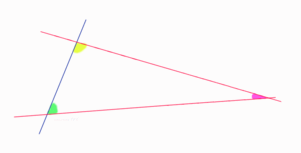Аксиома параллельности Евклида | это... Что такое Аксиома параллельности Евклида? (original) (raw)

Пересечения прямых (анимация)
Аксио́ма паралле́льности Евкли́да, или пя́тый постула́т — одна из аксиом, лежащих в основании классической планиметрии. Впервые приведена в «Началах» Евклида:[1]
И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньшие двух прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых.
Оригинальный текст (др.-греч.)
Καὶ ἐὰν εἰς δύο εὐθείας εὐθεῖα ἐμπίπτουσα τὰς ἐντὸς καὶ ἐπὶ τὰ αὐτὰ μέρη γωνίας δύο ὀρθῶν ἐλάσσονας ποιῇ, ἐκβαλλομένας τὰς δύο εὐθείας ἐπ' ἄπειρον συμπίπτειν, ἐφ' ἃ μέρη εἰσὶν αἱ τῶν δύο ὀρθῶν ἐλάσσονες.
Евклид различает понятия постулат и аксиома, не объясняя их различия; в разных манускриптах «Начал» Евклида разбиение утверждений на аксиомы и постулаты различно, равно как не совпадает и их порядок. В классическом издании «Начал» Гейберга сформулированное утверждение является пятым постулатом.
На современном языке текст Евклида можно переформулировать так[2]:
Если [на плоскости] при пересечении двух прямых третьей сумма внутренних односторонних углов меньше двух прямых, то эти прямые при достаточном продолжении пересекаются, и притом с той стороны, с которой эта сумма меньше двух прямых.
Уточнение, с какой именно стороны пересекаются прямые, Евклид добавил, вероятно, для ясности — легко доказать, что оно вытекает из самого факта существования пересечения[2].
Пятый постулат чрезвычайно сильно отличается от других постулатов Евклида, простых и интуитивно очевидных (см. Начала Евклида). Поэтому в течение двух тысячелетий не прекращались попытки исключить его из списка аксиом и вывести как теорему. Все эти попытки окончились неудачей. «Вероятно, невозможно в науке найти более захватывающую и драматичную историю, чем история пятого постулата Евклида»[3]. Несмотря на отрицательный результат, эти поиски не были напрасны, так как в конечном счёте привели к полному пересмотру научных представлений о геометрии Вселенной.
Содержание
- 1 Эквивалентные формулировки постулата о параллельных
- 2 Абсолютная геометрия
- 3 Попытки доказательства
- 4 Первые наброски неевклидовой геометрии
- 5 Открытие неевклидовой геометрии
- 6 Доказательство независимости пятого постулата
- 7 Примечания
- 8 Литература
- 9 Ссылки
Эквивалентные формулировки постулата о параллельных
В современных источниках обычно приводится другая формулировка постулата о параллельных, эквивалентная (равносильная) V постулату и принадлежащая Проклу[4] (за рубежом её часто называют аксиомой Плейфера):

Постулат Прокла
В этой формулировке слова «одну и только одну» часто заменяют на «только одну» или «не более одной», так как существование хотя бы одной такой параллельной сразу следует из теорем 27 и 28 «Начал» Евклида.
Вообще у V постулата имеется огромное количество эквивалентных формулировок, многие из которых кажутся довольно очевидными. Вот некоторые из них[5] [6] [7].
- Существует прямоугольник (хотя бы один), то есть четырёхугольник, у которого все углы прямые[8].
- Вариант: существует хотя бы 1 квадрат (правильный 4-угольник) с прямым внутренним углом.
- Существуют подобные, но не равные треугольники (аксиома Валлиса, 1693). И здесь достаточно, чтобы существовала хотя бы одна пара таких треугольников[8].
- Любую фигуру можно пропорционально увеличить.
- Вариант: существует по меньшей мере одна фигура, которую можно пропорционально увеличить.
- Существует треугольник сколь угодно большой площади.
- Прямая, проходящая через точку внутри угла, пересекает по крайней мере одну его сторону (аксиома Иоганна Фридриха Лоренца, 1791).
- Через каждую точку внутри острого угла всегда можно провести прямую, пересекающую обе его стороны (одно из предположений Лежандра, 1800).
- Сближающиеся прямые рано или поздно пересекутся.
- Варианты: не существует 2 асимптотически сближающихся прямых.
- перпендикуляр и наклонная к одной и той же прямой непременно пересекаются. Утверждение известно как постулат Лежандра, хотя эта формулировка встречалась ещё в XIII веке у ат-Туси.
- Точки, равноудалённые от данной прямой (по одну её сторону), образуют прямую.
- Если две прямые начали сближаться, то невозможно, чтобы они затем начали (в ту же сторону, без пересечения) расходиться (аксиома Роберта Симсона, 1756).
- Вариант: Если две прямые в одну сторону расходятся, то в другую — сближаются.
- Если 2 прямые параллельны, то длина перпендикуляра, опущенного из любой точки одной из этих прямых на другую, всегда одинакова для данной пары прямых. Это означает, неформально говоря, что расстояние между параллельными прямыми всегда постоянно, то есть параллельные прямые не могут ни сближаться, ни расходиться.
- Сумма углов одинакова у всех треугольников.
- Вариант: существует, как минимум, одна пара неравновеликих треугольников с одинаковой суммой углов.
- Существует треугольник (по меньшей мере один), сумма углов которого равна двум прямым[8].
- Вариант: существует N-угольник, сумма углов которого равна 180°*(N-2).
- Две прямые, параллельные третьей, параллельны и друг другу (аксиома Остроградского, 1855).
- Линия, ортогональная некоторому семейству параллельных прямых, является прямой.
- Прямая, пересекающая одну из параллельных прямых, непременно пересечёт и другую.
- Через любые три точки можно провести либо прямую, либо окружность.
- Вариант: для всякого невырожденного треугольника существует описанная окружность (аксиома Фаркаша Бойяи).
- Справедлива теорема Пифагора (как минимум в одном прямоугольном треугольнике).
- Вариант: пространство имеет Евклидову метрику.
- Отношение длины окружности к её диаметру является константой, то есть одинаково для любой окружности.
- Вариант: отношение длины окружности к её диаметру равно числу Пи (хотя бы у одной окружности).
Эквивалентность их означает, что все они могут быть доказаны, если принять V постулат, и наоборот, заменив V постулат на любое из этих утверждений, мы сможем доказать исходный V постулат как теорему.
Если вместо V постулата допустить, что для пары точка—прямая V постулат неверен, то полученная система аксиом будет описывать геометрию Лобачевского. Понятно, что в геометрии Лобачевского все вышеперечисленные эквивалентные утверждения неверны.
Система аксиом сферической геометрии требует изменения также и других аксиом Евклида.[9].
Пятый постулат резко выделяется среди других, вполне очевидных, он больше похож на сложную, неочевидную теорему. Евклид, вероятно, сознавал это, и поэтому первые 28 предложений в «Началах» доказываются без его помощи.
«Евклиду безусловно должны были быть известны различные формы постулата о параллельных».[4] Почему же он выбрал приведенную, сложную и громоздкую? Историки высказывали различные предположения о причинах такого выбора. В. П. Смилга полагал, что Евклид такой формулировкой указывал на то, что данная часть теории является незавершённой[10]. М. Клайн обращает внимание на то, что пятый постулат Евклида имеет локальный характер, то есть описывает событие на ограниченном участке плоскости, в то время как, например, аксиома Прокла утверждает факт параллельности, который требует рассмотрения всей бесконечной прямой.[11] Надо пояснить, что античные математики избегали использовать актуальную бесконечность; например, второй постулат Евклида утверждает не бесконечность прямой, а всего лишь то, что «прямую можно непрерывно продолжать». С точки зрения античных математиков, вышеприведенные эквиваленты постулата о параллельных могли казаться неприемлемыми: они либо ссылаются на актуальную бесконечность или (ещё не введенное) понятие измерения, либо тоже не слишком очевидны. Ещё одну версию выдвинул историк Имре Тот[12]: евклидова формулировка, возможно, была вначале (ошибочно доказанной) теоремой у кого-то из предшественников Евклида, и когда убедились, что доказать её не удаётся, статус теоремы повысили до постулата, не меняя текста формулировки.
Абсолютная геометрия
Если из списка аксиом исключить V постулат, то полученная система аксиом будет описывать так называемую абсолютную геометрию. В частности, первые 28 теорем «Начал» Евклида доказываются без использования V постулата и поэтому относятся к абсолютной геометрии. Для дальнейшего отметим две теоремы абсолютной геометрии:
- Параллельные прямые существуют; это следует из теорем 27 и 28 «Начал» Евклида.
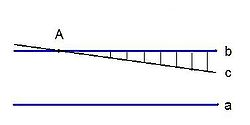
- При продолжении двух прямых от точки их пересечения расстояние между ними неограниченно возрастает[13].
Попытки доказательства
Математики с давних времён пытались «улучшить Евклида» — либо исключить пятый постулат из числа исходных утверждений, то есть доказать его, опираясь на остальные постулаты и аксиомы, либо заменить его другим, столь же очевидным, как другие постулаты. Надежду на достижимость этого результата поддерживало то, что IV постулат Евклида (все прямые углы равны) действительно оказался лишним — он был строго доказан как теорема и исключён из перечня аксиом.[5]
За два тысячелетия было предложено много доказательств пятого постулата, но в каждом из них рано или поздно обнаруживался порочный круг: оказывалось, что среди явных или неявных посылок содержится утверждение, которое не удаётся доказать без использования того же пятого постулата.

Доказательство Прокла
Прокл (V век н. э.) в «Комментарии к I книге Начал Евклида» сообщает, что такое доказательство предложил Клавдий Птолемей, критикует его доказательство и предлагает своё собственное.[13] В несколько упрощённом виде его можно описать так: пусть прямая  проходит через заданную точку
проходит через заданную точку  параллельно прямой
параллельно прямой  ; докажем, что любая другая прямая
; докажем, что любая другая прямая  , проведенная через ту же точку, пересекается с прямой
, проведенная через ту же точку, пересекается с прямой  . Как упоминалось выше, расстояние между прямыми от точки их пересечения возрастает неограниченно (ещё раз подчеркнём, что доказательство этой теоремы не опирается на V постулат). Но тогда в конце концов расстояние между
. Как упоминалось выше, расстояние между прямыми от точки их пересечения возрастает неограниченно (ещё раз подчеркнём, что доказательство этой теоремы не опирается на V постулат). Но тогда в конце концов расстояние между  и
и  превысит расстояние между параллельными прямыми, то есть прямые
превысит расстояние между параллельными прямыми, то есть прямые  и
и  пересекутся.
пересекутся.
Приведенное доказательство опирается на допущение, что расстояние между двумя параллельными прямыми постоянно (или, по крайней мере, ограничено). Впоследствии выяснилось, что это допущение равносильно V постулату.
Учёный I века до н. э. Посидоний предложил определить параллельные как прямые, на всём протяжении равноудалённые друг от друга. Из такого определения легко выводится пятый постулат. Однако определение Посидония некорректно: ниоткуда не следует, что линия, равноудалённая от данной прямой, есть прямая[14].
После упадка античной культуры V постулатом занялись математики стран ислама. Доказательство ал-Джаухари, ученика ал-Хорезми (IX век) [15], неявно подразумевало: если при пересечении двух прямых какой-либо третьей накрест-лежащие углы равны, то то же имеет место при пересечении тех же двух прямых любой другой. И это допущение равносильно V постулату.
Сабит ибн Курра (IX век) дал два доказательства; в первом он опирается на предположение, что если две прямые удаляются друг от друга с одной стороны, они обязательно приближаются с другой стороны. Во втором, как и Посидоний, он исходит из существования равноотстоящих прямых, причём этот факт ибн Курра пытается вывести из представления о «простом движении», т. е. о равномерном движении на фиксированном расстоянии от прямой (ему представляется очевидным, что траектория такого движения — тоже прямая) [16]. Каждое из двух упомянутых утверждений Ибн Курры эквивалентно V постулату.
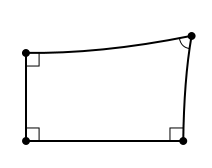
Четырёхугольник Ламберта
Аналогичную ошибку сделал ибн ал-Хайсам, но он впервые рассмотрел фигуру, позже получившую название «четырёхугольник Ламберта» — четырёхугольник, у которого три внутренних угла — прямые. Он сформулировал три возможных варианта для четвёртого угла: острый, прямой, тупой. Обсуждение этих трёх гипотез, в разных вариантах, многократно возникало в позднейших исследованиях.
Поэт и математик Омар Хайям подверг критике попытки ввести в геометрию механическое движение. Он предложил заменить V постулат на другой, более простой: две сходящиеся прямые пересекаются, и невозможно, чтобы две сходящиеся прямые расходились в направлении схождения. Каждая из двух частей этого утверждения равносильна постулату Евклида [17].
Ал-Абхари предложил доказательство, сходное с доказательством ал-Джаухари. (Это доказательство приводит в своей книге ас-Самарканди, и ряд исследователей считал его доказательством ас-Самарканди.) Он исходит из верного в абсолютной геометрии утверждения о том, что для всякой прямой, пересекающей стороны данного угла, может быть построена ещё одна прямая, пересекающая стороны этого же угла и отстоящая от его вершины дальше, чем первая. Но из этого утверждения он делает логически необоснованный вывод о том, что через всякую точку внутри данного угла можно провести прямую, пересекающую обе стороны этого угла, — и основывает на этом последнем утверждении, эквивалентном V постулату, всё дальнейшее доказательство.
Насир ад-Дин ат-Туси предложил построение, аналогичное построению Омара Хайяма [18]. Отметим, что сочинения ат-Туси стали известны Джону Валлису, и тем самым сыграли роль в развёртывании исследований по неевклидовой геометрии в Европе.
Первую в Европе известную нам попытку доказательства аксиомы параллельности Евклида предложил живший в Провансе (Франция) Герсонид (он же Леви бен Гершом, XIV век). Его доказательство опиралось на утверждение о существовании прямоугольника [19].
К XVI веку относится доказательство учёного-иезуита Христофора Клавиуса. Доказательство его, как и у ибн Курры, основывалось на утверждении, что линия, равноотстоящая от прямой — тоже прямая [20].
Валлис в 1693 году в одной из своих работ воспроизводит перевод сочинения ат-Туси и предлагает эквивалентную, но более простую формулировку: существуют подобные, но не равные фигуры [21]. Клеро в своих «_Началах геометрии_» (1741), как и Герсонид, вместо V постулата взял его эквивалент «существует прямоугольник».
В целом можно сказать, что все перечисленные попытки принесли немалую пользу: была установлена связь между V постулатом и другими утверждениями, были отчётливо сформулированы две альтернативы V постулату — гипотезы острого и тупого угла.
Первые наброски неевклидовой геометрии

Сочинение Саккери
Глубокое исследование V постулата, основанное на совершенно оригинальном принципе, провёл в 1733 году итальянский монах-иезуит, преподаватель математики Джироламо Саккери. Он опубликовал труд под названием «_Евклид, очищенный от всех пятен, или же геометрическая попытка установить самые первые начала всей геометрии_». Идея Саккери состояла в том, чтобы заменить V постулат противоположным утверждением, вывести из новой системы аксиом как можно больше следствий, тем самым построив «ложную геометрию», и найти в этой геометрии противоречия или заведомо неприемлемые положения. Тогда справедливость V постулата будет доказана от противного [22].
Саккери рассматривает всё те же три гипотезы о 4-м угле четырёхугольника Ламберта. Гипотезу тупого угла он отверг сразу по формальным соображениям. Легко показать, что в этом случае вообще все прямые пересекаются, а тогда можно заключить, что V постулат Евклида справедлив — ведь он как раз и утверждает, что при некоторых условиях прямые пересекаются. Отсюда делается вывод, что «_гипотеза тупого угла всегда целиком ложна, так как она сама себя разрушает_» [23].
После этого Саккери переходит к опровержению «гипотезы острого угла», и здесь его исследование гораздо интереснее. Он допускает, что она верна, и, одно за другим, доказывает целый ряд следствий. Сам того не подозревая, он продвигается довольно далеко в построении геометрии Лобачевского. Многие теоремы, доказанные Саккери, выглядят интуитивно неприемлемыми, но он продолжает цепочку теорем. Наконец, Саккери доказывает, что в «ложной геометрии» любые две прямые или пересекаются, или имеют общий перпендикуляр, по обе стороны от которого они удаляются друг от друга, или же удаляются друг от друга с одной стороны и неограниченно сближаются с другой. В этом месте Саккери делает неожиданный вывод: «_гипотеза острого угла совершенно ложна, так как противоречит природе прямой линии_» [24].
Видимо, Саккери чувствовал необоснованность этого «доказательства», потому что исследование продолжается. Он рассматривает эквидистанту — геометрическое место точек плоскости, равноотстоящих от прямой; в отличие от своих предшественников, Саккери понимает, что в рассматриваемом случае это вовсе не прямая. Однако, вычисляя длину её дуги, Саккери допускает ошибку и приходит к реальному противоречию, после чего заканчивает исследование и с облегчением заявляет, что он «_вырвал эту зловредную гипотезу с корнем_». К сожалению, пионерская работа Саккери, изданная посмертно, не обратила на себя того внимания математиков, которого заслуживала, и только спустя 150 лет (1889) его соотечественник Бельтрами обнаружил этот забытый труд и оценил его историческое значение.
Во второй половине XVIII века было опубликовано более 50 работ по теории параллельных. В обзоре тех лет (Г. С. Клюгель) исследуется более 30 попыток доказать V постулат и доказывается их ошибочность. Известный немецкий математик и физик И. Г. Ламберт, с которым Клюгель переписывался, тоже заинтересовался проблемой; его «Теория параллельных линий» была издана (как и труд Саккери, посмертно) в 1786 году.

Сферическая геометрия: все прямые пересекаются
Ламберт первым обнаружил, что «геометрия тупого угла» реализуется на сфере, если под прямыми понимать большие круги. Он, как и Саккери, вывел из «гипотезы острого угла» множество следствий, причём продвинулся гораздо дальше Саккери; в частности, он обнаружил, что дополнение суммы углов треугольника до 180° пропорционально площади треугольника.
В своей книге Ламберт проницательно отметил:[25]
Мне кажется очень замечательным, что вторая гипотеза [тупого угла] оправдывается, если вместо плоских треугольников взять сферические. Я из этого почти должен был бы сделать вывод — заключение, что третья гипотеза имеет место на какой-то мнимой сфере. Во всяком случае, должна же существовать причина, почему она на плоскости далеко не так легко поддаётся опровержению, как это могло быть сделано в отношении второй гипотезы.

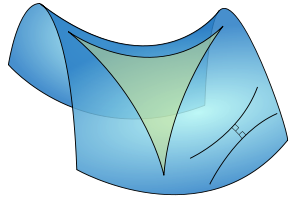
Геометрия на поверхности отрицательной кривизны
Ламберт не нашёл противоречия в гипотезе острого угла и пришёл к заключению, что все попытки доказать V постулат безнадёжны. Он не высказал каких-либо сомнений в ложности «геометрии острого угла», однако, судя по другому его проницательному замечанию, Ламберт размышлял о возможной физической реальности неевклидовой геометрии и о последствиях этого для науки[26]:
В этом есть что-то восхитительное, что вызывает желание, чтобы третья гипотеза была справедлива. И всё же я хотел бы <…>, чтобы это было не так, потому что это было бы сопряжено с целым рядом <…> неудобств. Тригонометрические таблицы стали бы бесконечно пространными, подобие и пропорциональность фигур не существовали бы вовсе <…>, астрономии пришлось бы плохо.
Замечательная работа Ламберта, как и книга Саккери, далеко опередила своё время и не вызвала интереса у тогдашних математиков. Та же судьба постигла «астральную геометрию» немецких математиков Ф. К. Швейкарта (1817) и Ф. А. Тауринуса (1826), по идеям близкую к построенной Ламбертом.
Тем временем попытки «смыть пятна» с Евклида продолжались (Луи Бертран, Лежандр, Семён Гурьев и другие). Лежандр дал целых три доказательства V постулата, ошибочность которых быстро показали его современники.[27] Последнее «доказательство» он опубликовал в 1823 году, за три года до первого доклада Лобачевского о новой геометрии.
Открытие неевклидовой геометрии
В первой половине XIX века по пути, проложенному Саккери, пошли сразу три математика: К. Ф. Гаусс, Н. И. Лобачевский и Я. Бойяи. Но цель у них была уже иная — не разоблачить неевклидову геометрию как невозможную, а, наоборот, построить альтернативную геометрию и выяснить её возможную роль в реальном мире. На тот момент это была совершенно еретическая идея; никто из учёных ранее не сомневался, что физическое пространство евклидово. Интересно, что Гаусса и Лобачевского учил в молодости один и тот же учитель — Мартин Бартельс, который, впрочем, сам неевклидовой геометрией не занимался.
Первым был Гаусс. Он не публиковал никаких работ на эту тему, но его черновые заметки и несколько писем однозначно подтверждают его глубокое понимание неевклидовой геометрии. Вот несколько характерных отрывков из писем Гаусса, где впервые в науке появляется термин «неевклидова геометрия»:[28]
Допущение, что сумма трёх углов треугольника меньше 180°, приводит к своеобразной, совершенно отличной от нашей (евклидовой) геометрии; эта геометрия совершенно последовательна, и я развил ее для себя совершенно удовлетворительно; я имею возможность решить в этой геометрии любую задачу, за исключением определения некоторой постоянной [кривизны], значение которой a priori установлено быть не может. Чем большее значение мы придадим этой постоянной, тем ближе мы подойдем к евклидовой геометрии, а бесконечно большое её значение приводит обе системы к совпадению. Предложения этой геометрии отчасти кажутся парадоксальными и непривычному человеку даже несуразными; но при строгом и спокойном размышлении оказывается, что они не содержат ничего невозможного. Так, например, все три угла треугольника можно сделать сколь угодно малыми, если только взять достаточно большие стороны; площадь же треугольника не может превысить, даже не может достичь некоторого предела, как бы велики ни были его стороны. Все мои старания найти в этой неевклидовой геометрии противоречие или непоследовательность остались бесплодными, и единственное, что в этой системе противится нашему разуму, это то, что в пространстве, если бы эта система была справедлива, должна была бы существовать некоторая сама по себе определенная (хотя нам и неизвестная) линейная величина. Но мне кажется, что мы, кроме ничего не выражающей словесной мудрости метафизиков, знаем очень мало или даже не знаем ничего о сущности пространства. (Из письма к Тауринусу, 1824)
В 1818 году в письме к австрийскому астроному Герлингу Гаусс выразил свои опасения:[29]
Я радуюсь, что вы имеете мужество высказаться так, как если бы Вы признавали ложность нашей теории параллельных, а вместе с тем и всей нашей геометрии. Но осы, гнездо которых Вы потревожите, полетят Вам на голову.
Ознакомившись с работой Лобачевского «Геометрические исследования по теории параллельных», Гаусс энергично ходатайствует об избрании русского математика иностранным членом-корреспондентом Гёттингенского королевского общества (что и произошло в 1842 году).

Евклид

Н. И. Лобачевский
Лобачевский и Бойяи проявили бо́льшую смелость, чем Гаусс, и почти одновременно (Лобачевский — в докладе 1826 года и публикации 1829 года; Бойяи — в письме 1831 года и публикации 1832 года), независимо друг от друга, опубликовали изложение того, что сейчас называется геометрией Лобачевского. Лобачевский продвинулся в исследовании новой геометрии дальше всех, и она в настоящий момент носит его имя. Но главная его заслуга не в этом, а в том, что он поверил в новую геометрию и имел мужество отстаивать своё убеждение (он даже предложил экспериментально проверить V постулат, измерив сумму углов треугольника). [30]
Во вступлении к своей книге «Новые начала геометрии» Лобачевский решительно заявляет:[31]
Всем известно, что в геометрии теория параллельных до сих пор оставалась несовершенной. Напрасное старание со времён Евклида, в продолжении двух тысяч лет, заставили меня подозревать, что в самых понятиях ещё не заключается той истины, которую хотели доказывать и которую проверить, подобно другим физическим законам, могут лишь опыты, каковы, например, астрономические наблюдения.<…> Главное заключение <…> допускает существование геометрии в более обширном смысле, нежели как ее представил нам первый Евклид. В этом пространном виде дал я науке название Воображаемой Геометрии, где как частный случай входит Употребительная Геометрия.
Трагическая судьба Лобачевского, подвергнутого остракизму в научном мире и служебном окружении за слишком смелые мысли, показала, что опасения Гаусса были не напрасны. Но и его борьба была не напрасна. По иронии судьбы торжество смелых идей Лобачевского обеспечил (посмертно) осторожный Гаусс. В 1860-е годы была опубликована переписка Гаусса, в том числе несколько восторженных отзывов о геометрии Лобачевского, и это привлекло внимание к трудам русского математика. В 1868 году выходит статья Э. Бельтрами, который показал, что плоскость Лобачевского имеет постоянную отрицательную кривизну (у евклидовой плоскости кривизна нулевая, у сферы — положительная); очень быстро неевклидова геометрия приобретает легальный научный статус, хотя всё ещё рассматривается как чисто умозрительная.
В конце XIX—начале XX века сначала математики (Бернхард Риман, Уильям Кингдон Клиффорд), а затем и физики (Общая теория относительности, Эйнштейн), окончательно покончили с догматом о евклидовой геометрии физического пространства.
Доказательство независимости пятого постулата
Доказать непротиворечивость новой геометрии ни Лобачевский, ни Бойяи не сумели — тогда математика ещё не располагала необходимыми для этого средствами. Только спустя 40 лет появились модель Клейна (1871) и модель Пуанкаре (1882), реализующие аксиоматику геометрии Лобачевского на базе евклидовой геометрии. Эти модели убедительно доказывают, что отрицание V постулата не противоречит остальным аксиомам геометрии; отсюда вытекает, что V постулат независим от остальных аксиом и доказать его невозможно.
Примечания
- ↑ Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.-Л.: ГТТИ, 1948. — Т. I. — С. 15.
- ↑ 1 2 Каган. Лобачевский, 1948, с. 164-165
- ↑ Смилга, 1988, с. 4
- ↑ 1 2 История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 110.
- ↑ 1 2 Мордухай-Болтовской Д. Д. Комментарии к «Началам» Евклида, книги I-VI. Указ. соч. — С. 241-244.
- ↑ Euclid’s Fifth Postulate
- ↑ Каган. Лобачевский, 1948, с. 167-175
- ↑ 1 2 3 Лелон-Ферран Ж., 1989, с. 255-256.
- ↑ Joel Castellanos. Non-Euclid. Axioms and Theorems (англ.). Архивировано из первоисточника 19 августа 2011. Проверено 11 февраля 2010.
- ↑ Смилга, 1988, с. 59-61
- ↑ Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 169.
- ↑ Tóth I. Das Parallelenproblem im Corpus Aristotelicum // Archive for history of exact sciences. — Berlin—Heidelberg—New York, 1967. — В. 4,5. — Т. 3. — С. 249-422.
- ↑ 1 2 Смилга, 1988, с. 72
- ↑ Лаптев Б. Л. Н. И. Лобачевский и его геометрия. — М.: Просвещение, 1976. — С. 71. — 112 с.
- ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — С. 231.
- ↑ Ибн Корра. Книга о том, что две линии, проведённые под углом, меньшим двух прямых, встречаются / Перевод и примечания Б. А. Розенфельда. — М.: ИМИ, 1963. — Т. XV. — С. 363—380.
- ↑ Хаййам. Трактаты / Перевод Б. А. Розенфельда. Редакция В. С. Сегаля и А. П. Юшкевича. Статья и комментарии Б. А. Розенфельда и А. П. Юшкевича. — М., 1962.
- ↑ Ат-Туси. Трактат, исцеляющий сомнение по поводу параллельных линий / Перевод Б. А. Розенфельда, примечания Б. А. Розенфельда и А. П. Юшкевича. — М.: ИМИ, 1960. — Т. XIII. — С. 483—532.
- ↑ Розенфельд Б. А. Доказательства пятого постулата Евклида средневековых математиков Хасана ибн ал-Хайсама и Льва Герсонида. — М.: ИМИ, 1958. — Т. XI. — С. 733—742.
- ↑ Clavius C. Euclidis Elementorum, libri XV. — Romae, 1574.
- ↑ Wallis. Opera mathematica, v. II. — Oxoniae, 1693. — С. 665.
- ↑ История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III. — С. 215-217.
- ↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. — Leipzig, 1895. — С. 100.
- ↑ G. Saccheri. Euklid von jedem Makel befreit. In: F. Engel, P. Stackel. Die Theorie der Parallellinien von Euklid bis auf Gauss, eine Urkundensammlung zur Vorgeschichte der Nicht-Euklidischen Geometrie. — Leipzig, 1895. — С. 105.
- ↑ Lambert J. H. Deutscher Gelehrter Briefwechsel. Bd. 1-5. Herausg. von J. Bernoulli. — Berlin, 1781—1784. — С. 202—203.
- ↑ Смилга, 1988, с. 121
- ↑ История математики, том III, стр. 218.
- ↑ Об основаниях геометрии, стр. 101-120.
- ↑ Об основаниях геометрии, с. 119—120.
- ↑ Лобачевский Н. И. Сочинения по геометрии (Полн. собр. соч., тт. 1—3). — М. — Л.: ГИТТЛ, 1946—1949.
- ↑ Об основаниях геометрии, с. 61-62.
Литература
- Начала Евклида / Перевод с греческого и комментарии Д. Д. Мордухай-Болтовского при редакционном участии М. Я. Выгодского и И. Н. Веселовского. — М.-Л.: ГТТИ, 1948.
- Текст книг I—VI на www.math.ru или на mccme.ru
- Вилейтнер Г. История математики от Декарта до середины XIX столетия. — М.: ГИФМЛ, 1960. — 468 с.
- Гильберт Д. Основания геометрии. — Л.: Сеятель, 1923. — 152 с.
- История математики с древнейших времён до начала XIX столетия. — М.: Наука, 1972.
- Каган В. Ф. Геометрия Лобачевского и её предыстория. — М.—Л., 1949.
- Каган В. Ф. Лобачевский. — Издание второе, дополненное. — М.-Л.: АН СССР, 1948. — 507 с.
- Лелон-Ферран Ж. Основания геометрии. — М.: Мир, 1989. — 312 с. — ISBN 5-03-001008-4
- Об основаниях геометрии. Сборник классических работ по геометрии Лобачевского и развитию её идей. — М., 1956.
- Розенфельд Б. А. История неевклидовой геометрии: Развитие понятия о геометрическом пространстве. — М.: Наука, 1976.
- Розенфельд Б. А., Юшкевич А. П. Теория параллельных линий на средневековом Востоке. — М.: Наука, 1983.
- Смилга В. П. В погоне за красотой. Занимательное введение в неевклидову геометрию. — 2-е изд. — М.: Молодая гвардия, 1988. — 288 с. — (Эврика).
- Успенский В. А. Апология математики. Глава 8. Параллельные прямые — в мифологии, реальности и математике. — М.: Амфора, 2009. — ISBN 978-5-367-00689-6
Ссылки
 |
Аксиома параллельности Евклида на Викискладе? |
|---|
- Александров А. Д. Тупость и гений. «Квант», №№ 11, 12 (1982). Архивировано из первоисточника 19 августа 2011. Проверено 9 октября 2009.
- Возникновение неевклидовой геометрии. Архивировано из первоисточника 19 августа 2011. Проверено 9 октября 2009.
- Пятый постулат Евклида. Архивировано из первоисточника 21 августа 2011. Проверено 9 октября 2009.