Когомологии | это... Что такое Когомологии? (original) (raw)
Гомоло́гия — одно из основных понятий алгебраической топологии. Замкнутая линия гомологична нулю, если она ограничивает кусок поверхности, который отделяется от неё, если мы произведём разрез по этой линии. Например, на сфере любая замкнутая линия является таковой, а на торе, хотя и сущeствуют гомологичные нулю замкнутые линии, но разрез по меридиану или параллели не приведет к отделению куска поверхности. Ниже мы рассмотрим более общие и строгие определения этого понятия.
Содержание
- 1 Симплициальные гомологии
- 2 Сингулярные гомологии
- 3 Гомологии с коэффициентами в произвольных группах
- 4 Когомологии
- 5 Относительные гомологии и точная гомологическая последовательность
- 6 Аксиомы Стинрода — Эйленберга
- 7 Экстраординарные гомологии
- 8 Литература
- 9 См. также
Симплициальные гомологии
Симплициальные гомологии определяются наиболее просто. Вначале определим некоторые понятия.
Симплексы и компле́ксы
Симплексом размерности k будем называть выпуклую оболочку точек 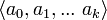 , таких, которые не лежат в каком-нибудь (k − 1)—мерном подпространстве. 0-мерный симплекс
, таких, которые не лежат в каком-нибудь (k − 1)—мерном подпространстве. 0-мерный симплекс 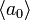 является точкой, 1-мерный
является точкой, 1-мерный 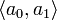 отрезком, 2-мерный
отрезком, 2-мерный 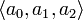 треугольником, 3-мерный
треугольником, 3-мерный 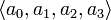 тетраэдром и т. д. Симплекс, порождённый частью точек
тетраэдром и т. д. Симплекс, порождённый частью точек 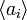 , называется гранью симплекса.
, называется гранью симплекса.
Далее вводится понятие симплициального компле́кса (с ударением на е). Компле́ксом K называется множество симплексов, причём с любым из которых в комплекс входят все его грани и любые два симплекса либо вообще не имеют общей точки, либо они пересекаются только по целой грани какой-то размерности, причем только по одной грани. Обычно требуют ещё, чтобы любая точка комплекса имела окрестность, пересекающуюся не более чем с конечным числом симплексов (т. н. локальная конечность).
Цепи комплексов
Мы будем рассматривать градуированную абелеву группу с целочисленными коэффициентами, порождённую симплексами комплекса, т. н. группу цепей C(K), являющуюся прямой суммой групп цепей размерности 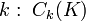 . Симплексы считаем имеющими ориентацию и симплекс
. Симплексы считаем имеющими ориентацию и симплекс 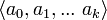 будем считать равным
будем считать равным 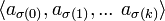 , если перестановка σ чётная и имеющим противоположный знак, если она нечётная.
, если перестановка σ чётная и имеющим противоположный знак, если она нечётная.
Грани цепи
Определим оператор взятия _i_-й грани:
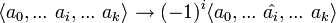 , где
, где 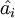 означает, что _i_-я вершина должна быть пропущена.
означает, что _i_-я вершина должна быть пропущена.
Этот оператор зависит только от самого симплекса, а не фиксированного порядка вершин. Для этого достаточно доказать, что оператор взятия _i_-й грани не изменится при перестановке двух вершин (транспозиции). Если эта транспозиция не затрагивает a i, то это очевидно. Если она переставляет a i на _j_-е место, то имеем (пусть, например, j < i):
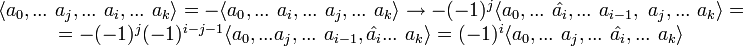
— что и ожидалось (возвращая 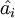 на старое место, надо сделать i − j + 1 транспозицию, соответственно столько же раз поменять знак).
на старое место, надо сделать i − j + 1 транспозицию, соответственно столько же раз поменять знак).
Определим оператор ориентированной границы симплекса следующим образом:
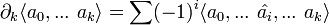
Независимость этого определения относительно перестановок вершин уже доказана, поэтому это определение строго. Взятие граничного оператора понижает размерность на 1. Для 0-мерного симплекса (точки) A считаем 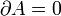 . По линейности распространим оператор
. По линейности распространим оператор 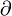 на любую цепь. Основным свойством граничного оператора является следующее:
на любую цепь. Основным свойством граничного оператора является следующее:
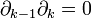
В результате применения  к симплексу
к симплексу 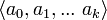 результатом будет цепь симплексов с двумя выброшенными вершинами. Предположим, что j < i. Симплекс
результатом будет цепь симплексов с двумя выброшенными вершинами. Предположим, что j < i. Симплекс 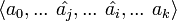 входит в результат первого действия оператора
входит в результат первого действия оператора 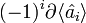 со знаком ( − 1)i + j, а в
со знаком ( − 1)i + j, а в 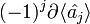 со знаком ( − 1)i + j − 1, так как по удалению
со знаком ( − 1)i + j − 1, так как по удалению 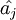 вершина
вершина 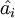 будет уже не на _i_—ом месте, а на (i − 1)—ом. Эти знаки противоположны, значит
будет уже не на _i_—ом месте, а на (i − 1)—ом. Эти знаки противоположны, значит  будет равен нулю для любого симплекса, а по линейности - для любой цепи.
будет равен нулю для любого симплекса, а по линейности - для любой цепи.
Симплициальные гомологии на комплексах и полиэдрах
Полиэдром (в широком смысле) называется множество, гомеоморфное комплексу. Этот гомеоморфизм называется триангуляцией. На комплексах и полиэдрах вводятся симплициальные гомологии следующим образом:
Рассмотрим группу цепей размерности k из симплексов нашего комплекса K, обозначаемую C k(K).
Цепь c, на которой значение граничного оператора 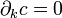 равно нулю (иначе говоря,
равно нулю (иначе говоря,  ) называется циклом; их множество обозначим Z k(K).
) называется циклом; их множество обозначим Z k(K).
Если для некоторой цепи c' выполняется 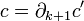 (иначе говоря,
(иначе говоря, 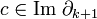 ), то цепь c называется границей; множество границ обозначим B k(K). Так как оператор
), то цепь c называется границей; множество границ обозначим B k(K). Так как оператор 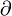 линеен, то и границы, и циклы образуют подгруппы группы цепей. Из того, что
линеен, то и границы, и циклы образуют подгруппы группы цепей. Из того, что  ясно, что любая граница является циклом, то есть,
ясно, что любая граница является циклом, то есть, 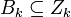 .
.
Две цепи называются гомологичными, если они отличаются на границу.Это записывается 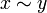 (то есть
(то есть 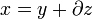 ).
).
Фактор-группа 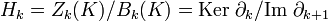 называется группой k-мерных симплициальных гомологий комплекса.
называется группой k-мерных симплициальных гомологий комплекса.
Пример
Пусть _S_1 - одномерный комплекс, являющийся границей двумерного симплекса (треугольника) 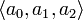 . Найдём его гомологии.
. Найдём его гомологии.
_B_1 = 0, так как в комплексе двумерных симплексов нет. Поэтому _H_1 = _Z_1 / _B_1 = _B_1. Узнаем теперь, когда одномерная цепь может быть циклом.
Возьмём произвольную цепь 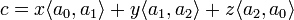 . Имеем:
. Имеем:
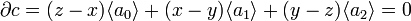 .
.
Значит, 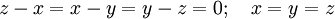 . Поэтому любой одномерный цикл c имеет вид
. Поэтому любой одномерный цикл c имеет вид

— значит _H_1 = _Z_1 есть просто бесконечная циклическая группа 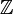 .
.
Найдём нульмерные гомологии. Так как 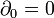 , то _Z_0 = _C_0. Из равенства
, то _Z_0 = _C_0. Из равенства 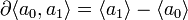 следует, что
следует, что 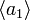 и
и 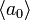 отличаются на границу. Аналогично
отличаются на границу. Аналогично 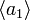 и
и 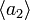 отличаются на границу, поэтому с точностью до границы любая нульмерная цепь имеет вид
отличаются на границу, поэтому с точностью до границы любая нульмерная цепь имеет вид  . То есть, _C_0является просто бесконечной циклической группой
. То есть, _C_0является просто бесконечной циклической группой  . Если она сама является границей, то есть
. Если она сама является границей, то есть 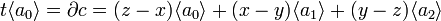 , то имеем, что
, то имеем, что  , поэтому _B_0 = 0 и
, поэтому _B_0 = 0 и 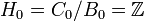 .
.
Итого, для границы двумерного симплекса 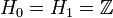 .
.
Некоторые свойства гомологий
Если гомологии комплекса K определены, то они же считаются гомологиями полиэдра | K | , соответствующего этому комплексу. Тут возникает проблема — данный полиэдр можно триангулировать по-разному. Однако можно доказать что непрерывному отображению полиэдров 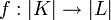 сооветствует гомоморфизм
сооветствует гомоморфизм 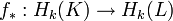 , причём это соответствие, как говорят, функториально, то есть произведению непрерывных отображений соответствует произведение гомоморфизмов групп гомологий (f g) * = f * g * , а тождественному отображению соответствует тождественный гомоморфизм (i d) * = i d * . Из этого следует, что группа гомологий полиэдра полностью определяется им самим.
, причём это соответствие, как говорят, функториально, то есть произведению непрерывных отображений соответствует произведение гомоморфизмов групп гомологий (f g) * = f * g * , а тождественному отображению соответствует тождественный гомоморфизм (i d) * = i d * . Из этого следует, что группа гомологий полиэдра полностью определяется им самим.
Если комплекс состоит из конечного числа симплексов, то группа гомологий будет иметь конечное число образующих. В этом случае она представляется в виде прямой суммы нескольких экземпляров группы целых чисел 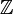 (их число, то есть ранг группы гомологий называется числом Бетти) и конечных циклических групп
(их число, то есть ранг группы гомологий называется числом Бетти) и конечных циклических групп 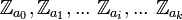 где каждое a i является делителем a i − 1 (эти числа называются коэффициентами кручения). Число Бетти и коэффициенты кручения определяются однозначно. Первоначально А.Пуанкаре как раз их и ввёл для характеристики топологических свойств. Э.Нётер показала важность перехода к изучению самих групп гомологий.
где каждое a i является делителем a i − 1 (эти числа называются коэффициентами кручения). Число Бетти и коэффициенты кручения определяются однозначно. Первоначально А.Пуанкаре как раз их и ввёл для характеристики топологических свойств. Э.Нётер показала важность перехода к изучению самих групп гомологий.
Сингулярные гомологии
Симплициальные гомологии были даны только для полиэдров, причём доказательство их инвариантности и функториальности довольно сложно. Сингулярные гомологии вводятся так, что их инвариантность и функториальность сразу становятся очевидными.
Пусть X — любое топологическое пространство. Сингулярный симплекс размерности k — это пара (Δ_k_,f) где Δ_k_ — это стандартный симплекс 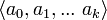 , а f — его непрерывное отображение в X;
, а f — его непрерывное отображение в X; 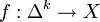 . Группу сингулярных цепей определим как множество формальных линейных комбинаций:
. Группу сингулярных цепей определим как множество формальных линейных комбинаций:
с целыми (обычно их полагают также ограниченными) коэффициентами z i. При этом для линейного отображения  определяемого перестановкой π точек
определяемого перестановкой π точек 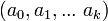 полагают
полагают 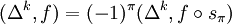 . Граничный оператор
. Граничный оператор 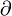 определяется на сингулярном симплексе (Δ_k_,f) так:
определяется на сингулярном симплексе (Δ_k_,f) так:
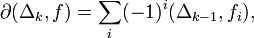
где Δ_k_ − 1 стандартный (k − 1)-мерный симплекс, а  , где ε_i_ — это его отображение на _i_-ю грань стандартного симплекса
, где ε_i_ — это его отображение на _i_-ю грань стандартного симплекса 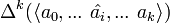 . Аналогично симплициальным гомологиям доказывается что
. Аналогично симплициальным гомологиям доказывается что  . Как и раньше вводятся понятия сингулярных циклов — таких цепей c k, что
. Как и раньше вводятся понятия сингулярных циклов — таких цепей c k, что 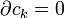 , и границ — цепей
, и границ — цепей  для некоторого c k + 1. Фактор-группа группы циклов по группе границ H k = Z k / B k называется группой сингулярных гомологий.
для некоторого c k + 1. Фактор-группа группы циклов по группе границ H k = Z k / B k называется группой сингулярных гомологий.
Пример
Найдём, к примеру, сингулярные гомологии пространства из одной точки X = * . Для каждой размерности существует только одно-единственное отображение 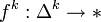 . Граница симплекса
. Граница симплекса 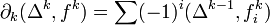 , где все
, где все 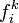 равны, так как отображают симплекс в одну точку (обозначим f k − 1). Значит:
равны, так как отображают симплекс в одну точку (обозначим f k − 1). Значит:
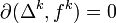 , если k нечетно (число членов в сумме четно, а знаки чередуются);
, если k нечетно (число членов в сумме четно, а знаки чередуются);
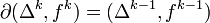 , если
, если 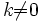 и четно;
и четно;
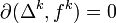 , если k = 0.
, если k = 0.
Отсюда получаем для нулевой размерности:  .
.
Для нечётной размерности  .
.
Для чётной размерности 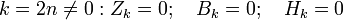 .
.
То есть группа гомологий равна 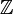 для нулевой размерности и равна нулю для всех положительных размерностей.
для нулевой размерности и равна нулю для всех положительных размерностей.
Можно доказать, что на множестве полиэдров сингулярные гомологии совпадают с ранее определенными симплициальными.
История
Сингулярные гомологии были введены Лефшецом.
Гомологии с коэффициентами в произвольных группах
Можно определять гомологии, позволяя коэффициентам при симплексах в цепях быть элементами любой абелевой группы G. Группы гомологий (симплициальные, сингулярные и т. д.) пространства X с коэффициентами в группе G обозначаются H k(X,G). Обычно применяют группу действительных чисел 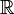 , рациональных чисел
, рациональных чисел 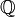 , или циклическую группу вычетов по модулю m —
, или циклическую группу вычетов по модулю m — 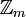 , причём обычно берётся m = p — простое число, тогда
, причём обычно берётся m = p — простое число, тогда 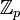 является полем.
является полем.
Когомологии
Кроме цепей можно ввести понятие коцепей — линейных форм на цепях со значением в группе G для каждой размерности  . Определяется граничный оператор
. Определяется граничный оператор  по формуле: (δ_k_ x)(c) = x(d k + 1_c_) (где xÎCk, cÎCk+1). Так как δ_k_ + 1δ_k_ = 0, а именно (δ_k_ + 1δ_k_(x))(c) = δ_k_ x(d k + 2_c_) = x(d k + 1_d_ k + 2_c_) = x(0) = 0. Поэтому аналогично тому, что было сказано выше, можно ввести понятия коциклов Z k(X,G) = K e r_δ_k, кограниц
по формуле: (δ_k_ x)(c) = x(d k + 1_c_) (где xÎCk, cÎCk+1). Так как δ_k_ + 1δ_k_ = 0, а именно (δ_k_ + 1δ_k_(x))(c) = δ_k_ x(d k + 2_c_) = x(d k + 1_d_ k + 2_c_) = x(0) = 0. Поэтому аналогично тому, что было сказано выше, можно ввести понятия коциклов Z k(X,G) = K e r_δ_k, кограниц 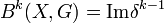 и когомологий H k(X,G) = Z k(X,G) / B k(X,G). Понятие когомологии двойственно понятию гомологии. Если G — кольцо, то в группе когомологий H * (X,G) определено естественное умножение (произведение Колмогорова — Александера или
и когомологий H k(X,G) = Z k(X,G) / B k(X,G). Понятие когомологии двойственно понятию гомологии. Если G — кольцо, то в группе когомологий H * (X,G) определено естественное умножение (произведение Колмогорова — Александера или 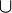 -npоизведение), превращающее эту группу в градуированное кольцо, называемое кольцо когомологий. В случае, когда X — дифференцируемое многообразие, кольцо когомологий
-npоизведение), превращающее эту группу в градуированное кольцо, называемое кольцо когомологий. В случае, когда X — дифференцируемое многообразие, кольцо когомологий 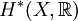 может быть вычислено при помощи дифференциальных форм на X (см. теорема де Рама). Понятие когомологии было введено Александером и Колмогоровым.
может быть вычислено при помощи дифференциальных форм на X (см. теорема де Рама). Понятие когомологии было введено Александером и Колмогоровым.
Относительные гомологии и точная гомологическая последовательность
Возьмём случай двух топологических пространств YÌ X; Группа цепей Ck(Y)Ì Ck(X) (цепи могут быть как с целочисленными коэффициентами, так и с коэффициентами в любой группе G). Относительными цепями будут называться элементы фактор группы Ck(X,Y)=Ck(X)/Ck(Y). Так как граничный оператор d на группе гомологий подпространства Y переводит dk:Ck(Y)→Ck-1(Y), то можно определить на фактор группе Ck(X,Y) граничный оператор (мы его также обозначим через d) dk:Ck(X,Y)→Ck-1(X,Y). Те относительные цепи, которые он переводит в 0 будут называться относительными циклами Zk(X,Y), а цепи, которые являются его значениями — относительными границами Bk(X,Y). Так как dd=0 на абсолютных цепях, то это же будет верно для относительных, отсюда Bk(X,Y)ÌZk(X,Y). Фактор-группа Hk(X,Y)=Zk(X,Y)/Bk(X,Y) называется группой относительных гомологий. Так как каждый абсолютный цикл в Hk(X) является также и относительным то имеем гомоморфизм jk:Hk(X)→Hk(X,Y). По функториальному свойству вложение ik:Y→X приводит к гомоморфизму i*:Hk(Y)→Hk(X). В свою очередь можно построить гомоморфизм d* k:Hk(X,Y)→Hk-1(Y), который мы определим следующим образом. Пусть сkÎCk(X,Y) — относительная цепь, которая определяет цикл из Hk(X,Y). Рассмотрим её как абсолютную цепь в Ck(X) (с точностью до элементов Ck(Y)). Так как это относительный цикл, то dkc будет равен нулю с точностью до некой цепи ck-1ÎCk-1(Y). Положим d* k равным классу гомологий ck-1=dkcÎZk-1(Y). Если мы возьмём другую абсолютную цепь c'kÎCk(X), определяющую тот же относительный цикл, то мы будем иметь c=c'+u, где uÎCk(Y). Имеем dkc=dkc'+dku, но так как dku является границей в Zk-1(Y) то dkc и dkc' определяют один и тот же элемент в группе гомологий Hk-1(Y). Если взять другой относительный цикл c", дающий тот же элемент в группе относительных гомологий c=c"+b, где b — относительная граница, то в силу того, что b граница для относительных гомологий b=dk+1x+v, где vÎCk(Y) , отсюда dkc=dkc"+dkdk+1x+dkv, но dd=0, а dkv — граница в Zk-1(Y). Поэтому класс гомологий d* kck определен однозначно. Ясно по линейности оператора d* k, что он является гомоморфизмом. Итак мы имеем гомоморфизмы: i* k:Hk(Y)→Hk(X); j* k:Hk(X)→Hk(X,Y) и d* k:Hk(X,Y)→Hk-1(Y);
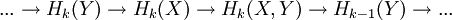
Можно доказать, что эта последовательность точна, то есть образ любого гомоморфизма равен ядру следующего гомоморфизма.
Аксиомы Стинрода — Эйленберга
Помимо уже известных нам симплициальных и сингулярных гомологий существуют ещё другие теории гомологий и когомологий, например клеточные гомологии, когомологии Чеха, когомологии де Рама и т.д. Стинрод и Эйленберг определили систему аксиом теории (ко)гомологий. Вначале они определяют т. н. допустимый класс пар D топологических пространств, удовлетворяющий следующим свойствам:
- Если (X, Y)∈D, то (X, X)∈D, (X,Æ)∈D, (Y, Y)∈D и (Y,Æ)∈D
- Если (X, Y)∈D, то и (X×I, Y×I)∈D, где I — замкнутый интервал [0,1]
- (*,Æ)∈D, где * — одноточечное пространство.
В теории гомологий по Стинроду-Эйленбергу каждой допустимой паре и любому целому числу k соответствует абелева группа Hk(X,Y) и непрерывному отображению пар f:(X,Y)→(X',Y') соответствует гомоморфизм f* k:Hk(X,Y)→Hk(X',Y') (Пространство X отождествляется с парой (X,Æ), а Hk(X) с Hk(X,Æ), причём выполняются следующие аксиомы:
- Тождественному отображению пары id соответствует тождественный гомоморфизм id* k
- (gf)* k=g* kf* k
(функториальные свойства) - Определен граничный гомоморфизм d* k:Hk(X,Y)→Hk-1(Y) причём если f:(X,Y)→(X',Y') то для соответствующего гомоморфизма f* k:Hk(X,Y)→Hk(X',Y') d* kf* k=f* k-1d* k для любой размерности k.
- Пусть i:Y→X и j:X→(X,Y) вложения, ik:Hk(Y)→Hk(X) и jk:Hk(X)→Hk(X,Y) — соответствующие гомоморфизмы, d* k:Hk(X,Y)→Hk-1(Y) — граничный гомоморфизм. Тогда определяемая ими последовательность
…→Hk(Y)→Hk(X)→Hk(X,Y)→Hk-1(Y)→… точна
(аксиома точности) - Если отображения f, g:(X,Y)→(X',Y') гомотопичны то соответствующие гомоморфизмы равны f* k=g* k для любой размерности k
(аксиома гомотопической инвариантности). - Если U⊂X — открытое подмножество X, причём его замыкание содержится во внутренности множества Y: (Ū⊂Int Y), тогда если пары (X\U, Y\U) и (X, Y) принадлежат допустимому классу, то для любой размерности k включению (X\U, Y\U)→(X, Y) соответствует изоморфизм Hk(X\U, Y\U)→Hk(X, Y)
(аксиома вырезания). - Для одноточечного пространства Hk(*)=0 для всех размерностей k>0. Абелева группа G=H0(*) называется группой коэффициентов
(аксиома размерности).
Для сингулярных гомологий допустимый класс пар состоит из всех пар топологических пространств. Ранее определенные группы сингулярных гомологий с коэффициентами в группе G их отображения и граничный гомоморфизм d* удовлетворяют всем этим аксиомам. Если в качестве допустимого класса взять класс полиэдров, то можно доказать, что гомологии, определенные с помощью данной системы аксиом, совпадают с симплициальными.
Аналогично можно ввести систему аксиом для когомологий, которая полностью аналогична. Необходимо только иметь в виду, что отображению f: (X, Y)→(X', Y') соответствует f* k: Hk(X', Y')→Hk(X, Y) (контравариантность) и что кограничный гомоморфизм δ* k:Hk-1(Y)→Hk(H, Y) увеличивает размерность.
Экстраординарные гомологии
В системе аксиом Стинрода — Эйленберга аксиома размерности оказывается не столь важна, как остальные. Теории (ко)гомологий, которые могут иметь ненулевые группы (ко)гомологий одноточечного пространства для размерностей k>0, называются экстраординарными или обобщёнными. Наиболее важными экстраординарными теориями являются K-теория Атьи (надо отметить важный вклад в эту теорию Хирцебруха, Ботта и Адамса) и теория бордизмов Р.Тома.
Литература
- Вик Дж. У. Теория гомологий. Введение в алгебраическую топологию. — М.: МЦНМО, 2005
- Дольд А. Лекции по алгебраической топологии. — М.: Мир, 1976
- Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия: Методы теории гомологий. — М.: Наука, 1984
- Зейферт Г., Трельфалль В. Топология. — Ижевск: РХД, 2001
- Лефшец С. Алгебраическая топология. — М.: ИЛ, 1949
- Новиков П. С. Топология. — 2 изд. испр. и доп. — Ижевск: Институт компьютерных исследований, 2002
- Прасолов В. В. Элементы теории гомологий. — М.: МЦНМО, 2006
- Свитцер Р. М. Алгебраическая топология. — гомотопии и гомологии. — М.: Наука, 1985
- Спеньер Э. Алгебраическая топология. — М.: Мир, 1971
- Стинрод Н., Эйленберг С. Основания алгебраической топологии. — М.: Физматгиз, 1958
- Фоменко А. Т., Фукс Д. Б. Курс гомотопической топологии. — М.: Наука, 1989
См. также
- Гомологическая алгебра
- Гомотопия
Wikimedia Foundation.2010.