Deciphering the Structure and Function of Nuclear Pores using Single Molecule Fluorescence Approaches (original) (raw)
. Author manuscript; available in PMC: 2017 May 22.
Published in final edited form as: J Mol Biol. 2016 Mar 2;428(10 Pt A):2091–2119. doi: 10.1016/j.jmb.2016.02.023
Abstract
Due to its central role in macromolecular trafficking and nucleocytoplasmic information transfer, the nuclear pore complex (NPC) has been studied in great detail using a wide spectrum of methods. Consequently, many aspects of its architecture, general function and role in the life cycle of a cell are well understood. Over the last decade, fluorescence microscopy methods have enabled the real-time visualization of single molecules interacting with and transiting through the NPC, allowing novel questions to be examined with nanometer precision. While initial single molecule studies focused primarily on import pathways using permeabilized cells, it has recently proven feasible to investigate the export of mRNAs in living cells. Single molecule assays can address questions that are difficult or impossible to answer by other means, yet the complexity of nucleocytoplasmic transport requires that interpretation be based on a firm genetic, biochemical, and structural foundation. Moreover, conceptually simple single molecule experiments remain technically challenging, particularly with regards to signal intensity, signal-to-noise ratio, and the analysis of noise, stochasticity, and precision. We discuss nuclear transport issues recently addressed by single molecule microscopy, evaluate the limits of existing assays and data, and identify open questions for future studies. We expect that single molecule fluorescence (SMF) approaches will continue to be applied to outstanding nucleocytoplasmic transport questions, and that the approaches developed for NPC studies are extendable to additional complex systems and pathways within cells.
Keywords: nuclear pore complex, nucleocytoplasmic transport, single molecule fluorescence, protein import, mRNA export
GRAPHICAL ABSTRACT
INTRODUCTION
With the evolution of eukaryotes and the cell nucleus, a demand arose for the exchange of material, information and energy between the cytoplasm and nucleus. From yeast to man, cells have controlled gates within the nuclear double membrane called nuclear pore complexes (NPCs), which contain a semi-permeable barrier and have distinct architectural features at the nucleoplasmic and cytoplasmic exits. Though NPCs were long considered the only conduits between the nucleus and the cytoplasm, the egress of “mega-RNPs” via a budding mechanism was recently described.1,2 Nonetheless, the vast majority of nucleocytoplasmic traffic occurs via NPCs. Some of the most striking features of NPCs are that they catalyze rapid bi-directional transport (milliseconds), they transport cargos ranging in size from small to very large (up to ~40 nm in diameter), they are stably integrated into the nuclear envelope (NE) during interphase but disassemble and re-assemble during mitosis, and they execute regulatory functions in gene expression.3-8 This Special Review Issue of the Journal of Molecular Biology (JMB) summarizes some of the latest structural and mechanistic findings about NPCs and nucleocytoplasmic transport mechanisms. Here, we discuss questions recently addressed by single molecule fluorescence (SMF) microscopy approaches. But first, we briefly outline the structural and transport properties of NPCs. The reader is referred to other reviews in this Issue for more detailed information regarding these properties.
The NPC Structure: An Overview
NPCs are large (~60-120 MDa) structures composed of at least 30 different nuclear pore proteins called nucleoporins (Nups). Based on the octagonal rotational symmetry of an NPC, each Nup is thought to be present in integer multiples of eight.5,9-11 Eight flexible filaments extend ~30-50 nm into the cytoplasm. Eight thin filaments extend ~40-75 nm into the nucleoplasm and terminate in a ring to form a nuclear basket.10,12-14 Images of NPCs obtained by electron microscopy (EM) reveal a large hourglass-shaped central pore with a minimum diameter of ~40-50 nm and a length of ~40-95 nm (dimensions vary between species but are fairly constant within an organism – yeast NPCs have the smaller dimensions).13,15-17 The proteins that form the basic framework of the NPC’s core structure are termed ‘scaffold Nups.’ Despite the large central pore formed by the scaffold Nups, the NPC is largely impermeable to molecules larger than ~4-5 nm.18,19 The permeability barrier is generated by a network of ~200-250 intrinsically disordered polypeptide domains that occupy the central pore and decorate the cytoplasmic and nucleoplasmic exits.20-22 These disordered polypeptides contain, in aggregate, 3,000-4,000 phenylalanine-glycine (FG) repeats to which nuclear transport receptors (NTRs) transiently bind as they carry cargos through NPCs.11,23-27 This system of intrinsically disordered FG-containing polypeptides (FG-domains) is generically termed the FG-network. As the FG-network is a central focus of this review, its hierarchical organization bears repeating: the FG-network is composed of hundreds of FG-polypeptides (or FG-domains), each of which contains FG repeats (from a few to ~50 FG repeats/polypeptide).20
Transport Pathways
Cargos are transported through NPCs in both directions. These processes are choreographed via multiple transport pathways and a cast of nuclear transport factors. Small molecules (< ~20-40 kDa; diameter < ~4-5 nm) can transit NPCs relatively unhindered without specific recognition (passive diffusion or signal-independent transport). Larger cargos, however, require an active transport mechanism mediated by NTRs (also known as karyopherins). NTRs bind a nuclear localization signal (NLS) or a nuclear export signal, and the resultant NTR/cargo complexes readily migrate through NPCs (facilitated translocation or signal-dependent transport).4,28-31 NTRs are classified as importins or exportins, reflecting their ability to carry cargos into or out of the nucleus, respectively. In the nucleus, RanGTP promotes disassembly of import complexes, freeing the cargo and allowing NTRs to diffuse back to the cytoplasm.32 In the cytoplasm, export complexes containing RanGTP are disassembled upon activation of the RanGTPase by RanGAP and Ran binding proteins (RanBPs).33-35
The FG-Network
The FG-network has two main functions: it creates a permeability barrier that prevents the free flow of material through the large central pore created by the NPC scaffold, and it contains the binding sites (FG repeats) for NTRs, thereby generating selectivity. Each FG-Nup consists of a globular anchor domain, which is embedded in or attached to the NPC scaffold, and an intrinsically disordered domain of ~100 to ~1000 residues, which contains the FG repeats.20,36 FG-domains are generally considered to be flexible polymers that do not form ordered secondary structures. The hydrophobic FG repeats are typically separated by short (~10 to 20 amino acids) hydrophilic segments,37,38 resulting in a highly hydrated network, although the water molecules are likely highly ordered. The FG-network is sufficiently fluid and mobile such that it is rapidly displaced by cargos undergoing transport after which it reseals.39,40
What is the Biophysical Nature of the Permeability Barrier?
The fundamental biophysical nature of the FG-network remains unsolved. The two most widely cited models of the last decade are the polymer brush20,41 and hydrogel models,42,43 which can be considered as two extremes in the phase space describing the potential arrangements and properties of the FG-domains on the NPC scaffold.44 The polymer brush model postulates that the FG-domains are largely non-interacting, relatively extended and unentangled.20,40,41 The hydrogel model posits that the FG-domains exhibit significant interstrand affinity via interactions between FG repeats, which results in a cohesive network.39,42,43,45 A hybrid, two-gate model postulates brush-like structures on both cytoplasmic and nuclear sides of the NPC, suitable for binding and (dis)assembly reactions, and a central cohesive structure in the center of the pore that generates a permeability barrier.46 A similar hybrid model was postulated in a recent cryo-EM study.47 Polymer brush behavior depends critically on anchoring density and geometrical constraints,20 which are not known precisely due to the absence of a complete high-resolution structure of the NPC scaffold. In contrast, untethered Nup98 FG-domains can phase separate, even in a complex mixture such as the bacterial cytoplasm, yielding a material with permeability properties resembling authentic NPCs.48 A composite picture including brush-like and hydrogel-like regions depending on the local FG-polypeptide composition and density is consistent with these data.
Considering that the micromolar concentrations of NTRs inside a cell are typically higher than their affinities (low- to sub-micromolar _KD_’s) for FG-polypeptides in vitro,49 NPCs can be predicted to always contain high concentrations of NTRs.50 This is consistent with the finding that ~100 molecules of Imp β1 bind to each NPC during steady-state.51-53 Notably NPCs and NPC mimics (FG-polypeptide-decorated nanopores and FG-polypeptide hydrogels) are more selective against signal-independent cargos in the presence of NTRs.39,52,54 Thus, NTRs are likely to be an integral component of the permeability barrier. Further, the binding affinity of Imp β1 and NTF2 for FG-polypeptides becomes weaker (more transient) in the presence of excess Imp β1, indicating that the in vitro affinities of NTRs binding to empty FG-polypeptide arrangements does not likely reflect steady-state in vivo transport conditions.55-57 In fact, single molecule experiments have revealed that cargo transport efficiencies and rates are significantly modulated by NTR occupancy level of the FG-network.58 In the reduction-of-dimensionality model, increased selectivity is generated by molecular crowding of NTRs on the surface of FG-domains.50 In addition to crowding constraints, tightly bound NTRs reduce the concentration of free FG-repeats, which reduces the avidity for incoming cargo complexes, thus yielding weaker interactions and allowing for rapid transport.57 Thus, NTRs modulate the inherent properties of the FG-polypeptide distribution.
Multiple groups have sought to test these conceptual pictures of the FG-network using modeling approaches.59-69 Thus far, however, direct connections to experiments are generally lacking in these studies, primarily because the data needed for calibration of the modeling parameters are not available or are incomplete. Importantly, relatively small perturbations to initial conditions or parameters can significantly change the output and subsequent interpretation.70,71 Thus, the differences between various models can be small, and FG-domain arrangement, density, and cohesiveness can produce diverse behaviors in distinct regions of the NPC. For these reasons, high-precision measurements investigating various aspects of nucleocytoplasmic transport are required to obtain a clear understanding of the biophysical properties of the FG-network. Single molecule approaches are ideally suited to probe these properties.
FG-NETWORK PROPERTIES DEDUCED FROM SINGLE MOLECULE PROTEIN IMPORT/EXPORT STUDIES
Early single molecule studies on NPCs revealed a number of major findings. First, protein cargo complexes, as well as empty NTRs, generally spend ≤ ~10 ms within the central pore under active transport conditions.3,72 Thus, translocation is fast, allowing for hundreds of individual translocation events per second. It remains unverified in real-time experiments whether multiple cargo complexes occupy the central pore simultaneously, and, if so, whether simultaneous translocation in opposite directions can occur. EM data support this picture for smaller cargos, though this appears physically impossible in the case of very large cargos such as pre-ribosomal subunits. Second, not all interactions with the NPC result in translocation to the opposing compartment, i.e., the transport efficiency is < 1.58 This is readily understood considering the stochastic nature of translational diffusion, though assembly and disassembly reactions occurring at the entrance and exit of the NPC bias diffusion to some extent (see next section). And third, both transport time and transport efficiency are influenced by the identity and number of NTRs within the FG-network.58 These effects are poorly understood, but they most certainly arise from differences in properties of the FG-network and the rates of complex assembly and disassembly caused by the altered density or availability of NTRs or nuclear transport cofactors (such as RanGTP) at the NPC. The results of more recent single molecule studies of protein import and export are described below.
Complex Assembly and Disassembly
Early studies examining the import of single protein molecules through NPCs focused primarily on developing the technology to collect and analyze SMF and tracking data and on measuring basic physical parameters of the translocation process (i.e., the translocation time and transport efficiency).58,73-76 In these experiments, the time-integrated position of single protein molecules labeled with one or more dye molecules was estimated by fitting a two-dimensional (2D) Gaussian to the observed fluorescent spots, as is standard in single molecule fluorescence (SMF) microscopy experiments.77,78 This approach yields a sub-pixel tracking precision, typically on the order of ~10-30 nm.73,74,76,79,80 More recently, the spatial and temporal relationships between the series of molecular interactions required for nucleocytoplasmic transport have been examined in detail. Single molecule fluorescence resonance energy transfer (smFRET) measurements were the primary technical improvement used to monitor complex assembly and disassembly of protein cargos during the translocation event. A number of major findings were directly observed.
After import of the Imp β/Imp α/cargo complex, this complex needs to be disassembled, allowing the Imp β and Imp α molecules to return to the cytoplasm for another round of import and releasing the free cargo into the nucleoplasm. From ensemble studies with solubilized proteins, it was determined that RanGTP generates RanGTP/Imp β and Imp α/cargo complexes, i.e., RanGTP dissociates the Imp β/Imp α interaction, leaving the Imp α/cargo complex intact.81 In vitro, the nuclear basket nucleoporin Nup50 (Nup2 in yeast) catalyzes the dissociation of Imp α/cargo complexes.82-86 However, single molecule studies revealed that during real-time transport through intact NPCs, both CAS and RanGTP, in addition to Nup50, are required to dissociate Imp α/cargo complexes.87 CAS is the NTR that exports Imp α back to the cytoplasm. Notably, the smFRET experiments identified a novel CAS/Imp α/cargo complex (which presumably also includes RanGTP) that was not previously considered when analyzing nuclear import. This transient CAS/Imp α/cargo complex has a very short lifetime (< 1 ms), and it disassembles into Imp α/cargo or CAS/Imp α complexes,88 i.e., both productive (forward) and non-productive (reverse) reactions occur. These observations clearly establish that the NPC is more than simply a sum of its parts – there are emergent properties that are not readily predicted.
The RanGTP/CAS/Imp α export complex is disassembled on the cytoplasmic side of the NPC. smFRET experiments confirmed that this dissociation process is enhanced by RanBP1, and SUMO-RanGAP1,88 factors that are known to be required for RanGTPase activity.33,35,89 Unexpectedly, however, the SUMOylated and un-SUMOylated forms of RanGAP behaved similarly.88 This was surprising because RanGAP1 requires the SUMO moiety to bind to Nup358, a major component of the cytoplasmic filaments.89-91 Thus, RanGAP apparently can promote RanGTPase activity during random diffusional encounters at the cytoplasmic exit of the NPC. Access to the RanGTP/CAS/Imp α complex could occur, for example, if this complex accumulates at the surface of the FG-network. However, an alternative, and more likely, possibility is that RanGTP/CAS/Imp α complex dissociation occurs within a low density region of the FG-network, which allows ready access to freely diffusing particles. Since the RanGAP binding domain on Ran is partially shielded by the exportin in the RanGTP/CAS/Imp α complex,92,93 it is unclear how RanGAP alone could promote dissociation of this complex. In vitro, RanBP1 and RanGAP work together to activate the RanGTPase,33,35 suggesting that the RanBP1-like domains of Nup35894,95 may assist soluble RanGAP with promoting dissociation of RanGTP/CAS/Imp α complexes at the NPC. While SUMO-RanGAP1 bound to the cytoplasmic filaments undoubtedly contributes to promoting RanGTP hydrolysis, these data indicate that soluble RanGAP1 also functions at the NPC. This is another emergent property that was not predicted or suggested by in vitro experiments with soluble proteins.
Single particle tracking analysis of the smFRET data clearly illustrate that CAS/Imp α complexes form in the nuclear basket during import and disassemble in the cytoplasmic filament region during export.87,88 These (dis)assembly sites were determined to be ~170 nm apart (see Figure 1), consistent with the span between the cytoplasmic filament and nuclear basket structural motifs.12,14,96-98 While the FG-network is generally discussed with regards to its properties within the central pore where it forms the permeability barrier, these data raise the following question: what is the nature of the FG-polypeptide distribution in the regions of complex assembly and disassembly? Since a significant fraction of complexes return to the originating compartment even after fully crossing through the NPC and reaching these (dis)assembly regions, a reasonable assumption is that there are at least some FG-polypeptides in these regions providing the necessary binding sites to retain the complex at the NPC and promote the return trip. On the other hand, the FG-polypeptide density is unlikely to be as dense as it is within the permeability barrier, thus allowing freely diffusing (dis)assembly factors (e.g., RanGTP and RanGAP) to enter the FG-network, and to find and interact with bound complexes. Thus, the FG-polypeptide distribution is likely to be relatively sparse at the nucleoplasmic and cytoplasmic exits of the pore. These regions have been termed ‘vestibules’,99 and are considered general sites of complex assembly and disassembly (Figure 2).
Figure 1. Locations at which Imp α/CAS Complexes Assemble and Disassemble during Nuclear Import and Export, as Determined by smFRET.
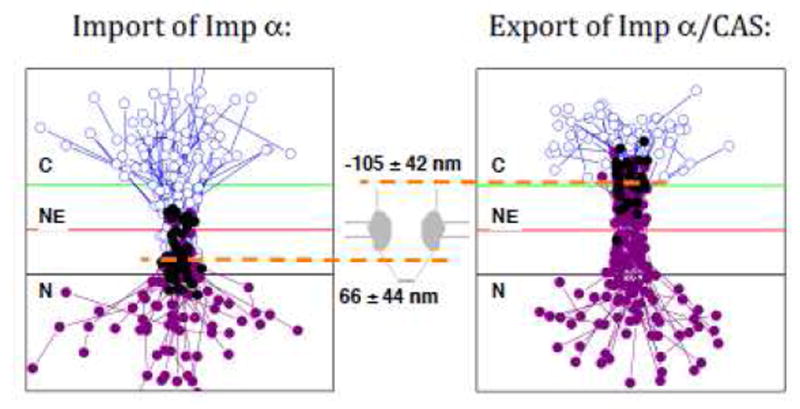
(Left) Trajectories in which Imp α (with donor dyes) bound to CAS (with acceptor dyes) during nuclear import, and then entered the nucleus. The positions of CAS-free Imp α are indicated by blue open circles, and the positions of Imp α/CAS complexes, as determined by smFRET, are identified by purple solid circles. The black solid circles identify the first location at which FRET was observed (N = 50). (Right) Trajectories in which Imp α/CAS complexes dissociated during nuclear export. Again, the positions of Imp α/CAS complexes, as determined by smFRET, are indicated by solid purple circles, and the positions of CAS-free Imp α are identified by blue open circles. In this case, however, the black solid circles identify the last location at which FRET was observed (N = 31). The orange dashed lines indicate the average location of Imp α/CAS complex assembly (in the nuclear basket) and disassembly (in the cytoplasmic filament region). For scale, the green and black lines are −100 and +100 nm from the NE. Trajectories from multiple NPCs were aligned and overlaid. Modified from reference 88.
Figure 2. Models of the Distribution and Density of the FG-polypeptides within NPCs and the Predicted Potential Energy within Various Regions.
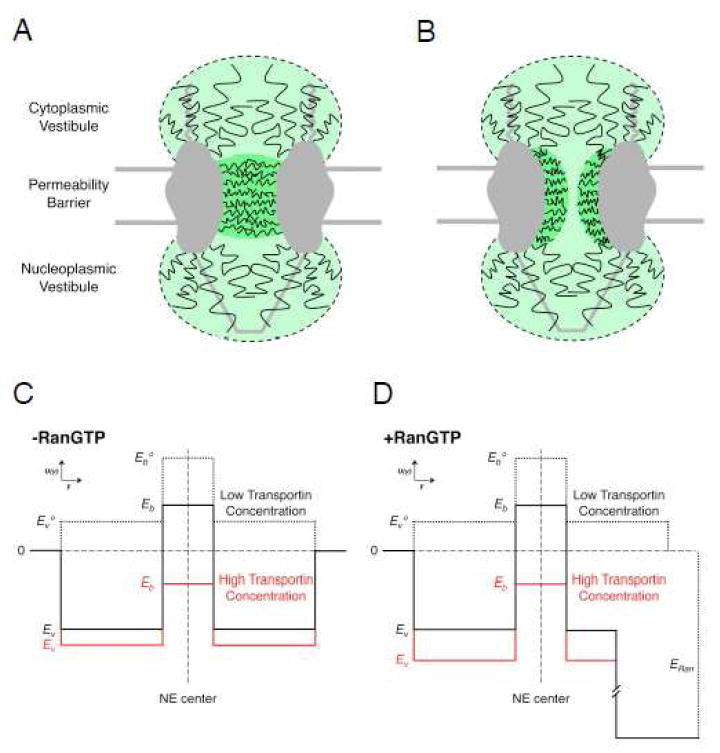
(A & B) FG-polypeptide distribution models. In these models, the permeability barrier is comprised of a relatively dense network of FG-polypeptides in the central pore, whereas the cytoplasmic and nucleoplasmic vestibules contain sparser distributions of FG-polypeptides. (A) An FG-network that completely occludes the central pore. (B) An FG-network with a relatively unoccluded region in the middle, which yields a ‘central channel’ for the passage of small, signal-independent cargos. (C & D) Double-well potential energy models. Based on the structural models in A & B, there is a significant free energy barrier for entry into the central pore, and a relatively low barrier for entering the cytoplasmic and nucleoplasmic vestibules (dashed black). The cargo M9-βGal requires multiple transportin molecules to efficiently lower and cross the central barrier (red), though binding and entry to the cytoplasmic vestibule is easily accomplished with a single transportin molecule (solid black). RanGTP promotes dissociation of import complexes, by strongly binding to the NTRs. This is modeled as a free energy sink in the nuclear basket region (D). Based on single molecule translocation times and transport efficiencies of M9-βGal, the vestibule well depth (Ev) is about -3 to -4 kB_T_, and the barrier heights (Eb) are about 1-2 and -1 kB_T_ at low and high concentrations of transportin, respectively. The barrier region width and vestibule widths are assumed to be 40 and 80 nm, respectively. Modified from reference 99.
Large Cargo Transport
The short interactions times (typically ≤ ~10 ms) observed in numerous single molecule experiments (summarized in references 72 and 3) are at least an order of magnitude shorter than the dissociation times (> 100 ms) predicted from in vitro measurements of FG-NTR affinities, which are ≤ ~2 μM (summarized in reference 49). Considering that the FG concentration within the permeability barrier is at least tens of millimolar,4,20 the apparent affinity of a cargo complex with two NTRs for this barrier is predicted to be sub-nanomolar due to avidity,99 with an off-time in the range of many minutes. Some cargos can have even more simultaneously bound NTRs – for example, nucleoplasmin is a pentamer, and thus has 5 NLSs.100 Clearly, extremely strong affinities are incompatible with rapid nucleocytoplasmic transport.49
These issues were examined in single molecule transport experiments using the large protein beta-galactosidase (βGal; 500 kDa) as a model cargo.99 The tetrameric M9-βGal with four M9 NLSs can simultaneously bind four NTRs. It was found that M9-βGal cargo complexes containing a single transportin (Imp β2) NTR transported 8-fold less efficiently than cargo complexes saturated with four Imp β2 molecules (3% vs. 24%). Thus, multiple bound NTRs enabled the βGal cargo to more easily penetrate the permeability barrier, consistent with earlier studies in which it was reported that multiple NLSs substantially improved translocation rates.100,101 Surprisingly, however, the interaction time for the two M9-βGal transport conditions differed by less than 2-fold (5 vs. 9 ms). It is not immediately obvious how the transport efficiency was increased substantially at higher transportin concentrations, presumably due to substantially more favorable interactions of the cargo complex with the permeability barrier, and yet the total NPC interaction time was minimally affected. A clue comes from the observation that the βGal cargo bound to one transportin molecule is found predominantly in the cytoplasmic vestibule region. With the concept of cytoplasmic and nucleoplasmic vestibules discussed in the previous section as a guide, a diffusion-based potential energy model was developed that is consistent with the βGal single molecule results. In short, the vestibules are energy wells, and the central FG-network generates a permeability (energy) barrier (Figure 2). Therefore, βGal cargo complexes spend most of the time in the vestibules (ideal for promoting complex (dis)assembly reactions) and little time is spent within the permeability barrier. Moreover, due to the lower density of FG-repeats in the vestibules, multivalent interactions are minimized, thus maintaining a low affinity interaction. This model predicts that the βGal cargo spends most of its time interacting with the NPC in the cytoplasmic vestibule bound by largely univalent interactions at both low and high transportin concentrations. Thus, interaction time depends little on the number of bound NTRs. Even though multivalent interactions within the permeability barrier are required for efficient transport of a large cargo, the overall affinity for the FG-network in this region remains weak due to the energy required to disrupt the FG-network (which includes entropic contributions from displacing the FG-polypeptides and enthalpic contributions from FG-polypeptide self-interactions). Crucially, the model predicts that the transportin interaction energy with an FG-polypeptide is maximally ~5-10 kB_T_, indicating an affinity of ~0.1-1 mM. Consistent with this model, millimolar FG-NTR affinities have been recently obtained with NMR experiments.102 Millimolar affinities are at least ~2 orders of magnitude weaker than FG-NTR affinities measured in most in vitro experiments (summarized in 49). Possible explanations for these discrepancies are that structural constraints within the FG-network limits the free accessibility of FG-repeats and/or that interaction energies are reduced by the energy required to displace FG-polypeptides.
For the double-well potential energy model described in Figure 2, the interaction energies within the vestibular and central barrier regions are dependent on the cargo complex – specifically, on its overall size, its surface properties, and the component NTR(s). These parameters determine the enthalpic (binding interactions, disruption of FG-polypeptide cohesive interactions) and entropic (volume constraints, FG-polypeptide displacements) contributions to the total interaction energy in the various regions. In the case of M9-βGal, the central region is a major barrier, and four transportin molecules are insufficient to lower the barrier height to the level of the vestibular binding energy.99 In contrast, the NLS-2xGFP/Imp α/Imp β cargo complex was observed primarily within the central pore region,73 indicating a single deep potential energy well. For a range of free NTRs and cargo complexes, particle distributions along the transport axis displayed single broad peaks, and particles were observed ~75 nm away from the pore center (on each side).75,76 These data are consistent with a deep central energy well, with shallow vestibules. While the βGal cargo presumably encounters a high central barrier due to its size, quantum dots (QDs) decorated with ~40 Imp β1 molecules (yielding cargo complexes of ~30 nm) were trapped within the central pore for tens of seconds,103 indicating that very large cargos decorated with a sufficiently high number of NTRs can collapse the central barrier.
Where is the Gate?
A major drawback of most SMF experiments is low emission intensity and photobleaching of the fluorescently-tagged molecule, which leads to insufficient precision and short trajectories. Ideal fluorescent tags would be extremely bright and stable, which would thus enable high-precision millisecond-scale particle tracking for many seconds to minutes. For these reasons, the brightness and photostability of QDs was used to investigate the substeps of nuclear import with high precision. QDs (~18 nm) were coated with ~40 Imp β1 binding (IBB) domains, yielding particles of ~30 nm that could be tracked with a precision of ~5-8 nm at 40 Hz (Figure 3A).103 Successful transport was achieved for 41% of NPC interactions and the mean cargo dwell time was ~120 s. QDs were mobile while bound to the NPC, and escape was rapid upon exit. The absence of RanGTP essentially completely (> 99%) blocked transport. The Ran-dependent gate was determined to be at the nucleoplasmic exit of the NPC. This gate was more thoroughly examined via direct stochastic optical reconstruction microscopy (dSTORM).52 In particular, it was found that there are at least two populations of Imp β1, a weaker binding population that exchanges in ~100 ms in the presence of RanGTP, and a strongly bound population that remains for ~3-4 min whose affinity is independent of RanGTP. Two distinct binding affinities for Imp β1 were also obtained in live cells, though in this case, both affinities indicate tight interactions (_KD_’s of ~0.3 and ~70 nM).51 In the dSTORM experiments,52 Imp β1 was found in two major pools, one each at the cytoplasmic and nucleoplasmic exits of the central pore (Figure 3B). Binding on the nucleoplasmic side was largely dependent on Nup153 and RanGTP. Knockdown of Nup153 increased the NPC permeability to both signal-independent and -dependent cargos and the absence of Imp β1 also increased permeability. It was therefore concluded that the combination of Imp β1 and Nup153 generates a nucleoplasmic gate, possibly as a size-filtering meshwork. The finding that NTRs generate a more selective barrier to inert cargo transport agrees with previous experimental and theoretical studies.39,54,64 In contrast, experiments with reconstituted Xenopus NPCs identified Nup98 as critical for creating the permeability barrier to both signal-independent and -dependent cargos,45 and deletion experiments in yeast identified a minimum of three or four central FG-polypeptides as essential for viability.25 The possibility exists that the permeability barrier is comprised of a combination of NTRs and FG-polypeptides that work together, and deletion or knock-down of any of a number of distinct components compromises the barrier.
Figure 3. Nuclear Import of Quantum Dots (QDs) and RanGTP Dependence of Imp β1 Localization.
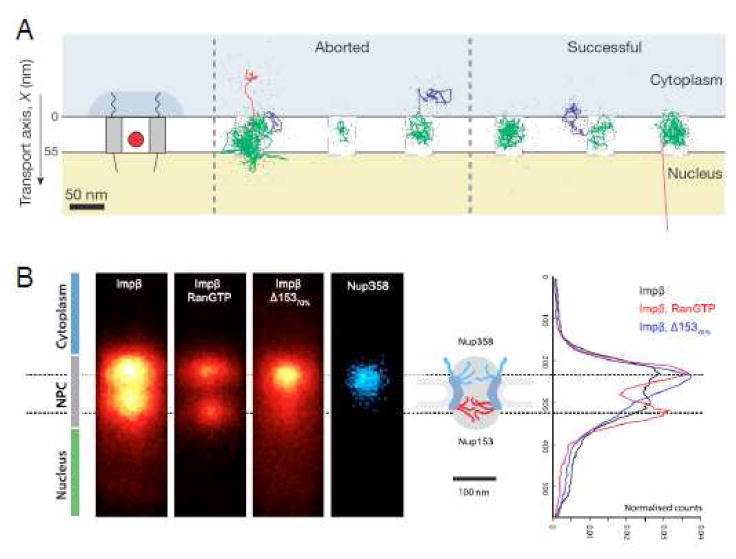
(A) Aborted and successful import trajectories for QDs (0.1 s running mean filtered). Substep coloring: docking events (blue), motion in the central pore (green) and undocking (red). (B) Localization of Imp β1 by dSTORM and its RanGTP-dependence. Δ153 signifies an siRNA knockdown of Nup153 (by 70%). Modified from references 103 and 52.
The pools of Imp β1 found at both exits of the central pore (Figure 3B)52 are consistent with the double-well/double-vestibule model (Figure 2). As discussed earlier, the depth of the energy wells and the height of the central barrier are cargo- and NTR-dependent for this model. Thus, for a free NTR such as Imp β1, the central energetic barrier could be low (or a shallow well), allowing fairly rapid exchange between the two bound pools of Imp β1. In the presence of RanGTP, which dissociates Imp β1 from the nucleoplasmic Nup153 binding sites, loss of Imp β1 from the cytoplasmic pool could therefore be a consequence of the equilibration between pools. According to this picture, RanGTP does not directly release the Imp β1 from the cytoplasmic pool. The long residence dwell time of QDs within the central pore103 implies a very deep potential well, much deeper than the vestibular wells, and consistent with the very large number (~40) of bound NTRs. Since the absence of RanGTP blocks QD transport (but not cytoplasmic release), there must be a nucleoplasmic barrier preventing exit from the deep central well. In contrast, it was not necessary to invoke a nucleoplasmic barrier to explain the transport behavior of βGal,99 another large cargo with multiple NLSs. The βGal data could also likely be explained by a model in which the densest FG-polypeptide distribution and the corresponding energy barrier is shifted towards the nuclear side of the pore. Alternatively, we note that the QD trajectories were assumed to be centered within the central pore, rather than aligned to an NE or NPC marker. Considering the high precision with which the QDs can be tracked and the very long trajectories, which allow the accessible space to be clearly established, it is a little puzzling that there are so many points located ‘within’ the NE (Figure 3A). More precisely, while trajectory points within the NPC central pore are expected, the large number of points outside the NPC scaffold in the NE region are unanticipated for such high resolution data as there is no known diffusion path between these regions. While NPC/NE positional fluctuations may contribute to broadening of the trajectories, particularly due to the long acquisition times, simulations to verify that such data are reasonable seem warranted. Note that due to the large size of the QD cargo complex, positional fluctuations relative to the central transport axis are expected to be on the order of a few nanometers. An alternate possibility, however, is that the central alignment assumption should be relaxed and that a greater portion of the QD trajectories should be positioned within the cytoplasmic vestibule. Presumably, a primary reason for this central alignment assumption was because fluorescent (YFP-Imp β1) NE localizations were highly variable. The recent finding of two pools of bound Imp β1 could largely explain this variability in NE localizations.52
Identifying Protein Import Pathways Through the FG-Network using SPEED
As indicated in the previous sections, the FG-network is inhomogeneous. Thus far, this inhomogeneity has been discussed in terms of differences in FG-polypeptide densities between the vestibules and the central permeability barrier. However, the permeability barrier itself is expected to be heterogeneous for at least two reasons. First, the FG-polypeptide density is likely to be variable. For example, an ~10 nm region in the center of the pore may be largely devoid of FG-polypeptides (Figure 2B), thus providing a conduit for the translocation of signal-independent cargos.50,104 Different packing densities may be influenced by the structural propensities of the individual FG-polypeptides.38 And second, different classes of FG-repeats (e.g., FxFG, GLFG, and FG) have different affinities for NTRs.105-109 The consequence of this heterogeneity is that different cargos can potentially migrate through different regions of the FG-network. This idea is supported by the differential transport defects observed with various yeast deletion mutants.25 These issues were examined using a high resolution particle tracking approach termed Single-Point Edge-Excitation Subdiffraction (SPEED) microscopy.79
In SPEED microscopy, the fluorescence excitation beam illuminates the sample at an angle of ~45° to the optical axis. 79 This illumination scheme is essentially the same as that described earlier for Highly Inclined and Laminated Optical Sheet (HILO) microscopy.51 The advantage of this off-axis illumination is that the signal-to-background ratio is increased ~3-fold compared to wide-field excitation because of the substantially reduced fluorescence excitation in the regions above and below the focal plane in the imaging cone.51 With high excitation intensities (500 kW/cm2), a time resolution as fast as 0.4 ms has been demonstrated,79 allowing for very rapid tracking of particles. A second focused and similarly aligned excitation beam illuminates only a single fluorescently-tagged NPC, enabling localization of the NPC and the tracked particle by alternating between the two illumination wavelengths.79 A key outcome of the SPEED approach is the generation of a three-dimensional (3D) probability map from two-dimensional (2D) xy tracking data, assuming a cylindrically symmetrical distribution (Figure 4). To do so, a cylindrically symmetric 3D spatial distribution model is hypothesized from which two-dimensional (2D) projections are calculated and fit to the experimental data. Note that no _z_-axis (optical axis) positional information is measured at any time. Therefore, generation of individual 3D trajectories is not possible.
Figure 4. SPEED Analysis.
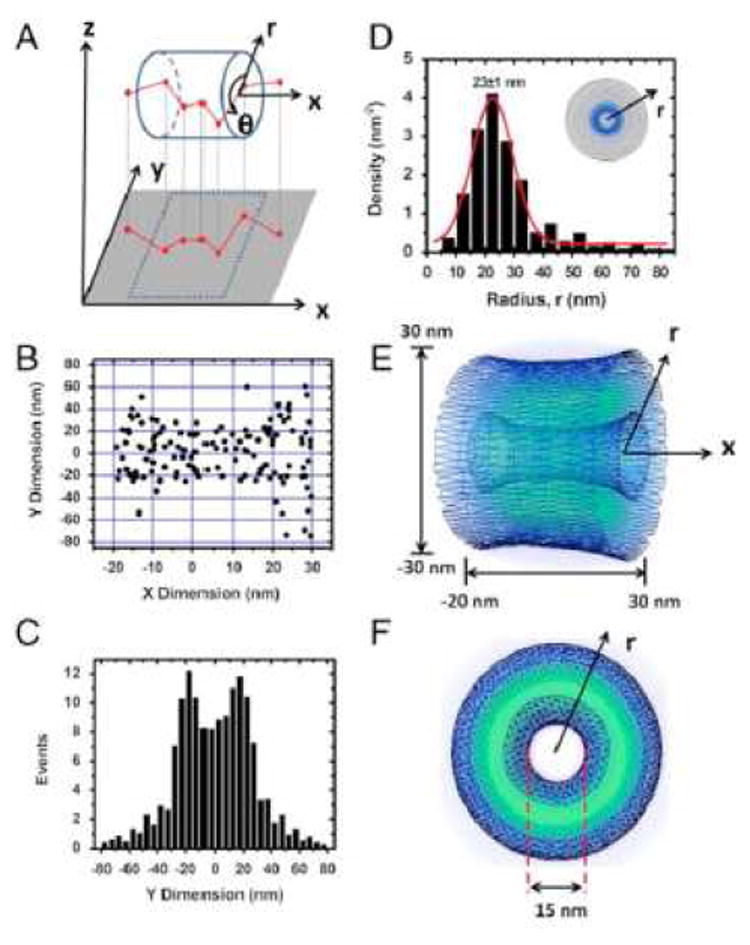
(A) Coordinate system used to describe the projection of a 3D trajectory into a 2D image. (B) Two-dimensional spatial locations of Imp β1 in the central pore obtained by SPEED microscopy. (C) Histogram of Imp β1 locations in the central pore region along the y dimension. (D) Histogram of spatial densities along the radial direction obtained by the SPEED coordinate transformation procedure. (E and F) The obtained 3D spatial densities of Imp β1. Brighter colors indicates higher densities. Reproduced from reference 79.
Using the SPEED approach, it was concluded that empty or cargo-carrying Imp β1 is generally located at the periphery of the central pore.79 A similar distribution pattern was obtained for transportin and NTF2.110 These results agree with EM data obtained from yeast cells in which Kap104 and Kap121 cargos were found near the periphery of the central pore.111 In contrast, again using the SPEED approach, small signal-independent cargos were concluded to transit through a central channel ~18 nm in diameter.110,27Note that we use the term ‘central pore’ (or ‘pore’) to describe the ~50 nm diameter opening in the center of the NPC that is observed in EM images,13,15-17 and the term ‘central channel’ to describe a hypothesized passageway in the center of the FG-network. Using the SPEED approach, the width of this central channel increases approximately 1.7-fold at high Imp β concentrations (15 µM),110 consistent with NTR-induced compaction of the FG-polypeptides along the scaffold walls.40,50,55 Based on a comparison of the expected and actual translocation times of signal-independent cargos, the effective viscosity in the central channel was estimated as ~3.4 cP for cargos < ~3 nm in diameter and ~1.6 cP for molecules ~3-7 nm in diameter. Since water has a viscosity of 1 cP, it was concluded that the central channel is filled with a complex, inhomogeneous and viscous medium rather than being an open aqueous conduit.110 However, cargo interactions with the ‘squishy’ walls of a channel (that likely has hydrophobic patches) can certainly significantly reduce translocation times, and transport is not truly one-dimensional, as assumed. Thus, a relatively open central channel is not ruled out by these data. Moreover, a completely open central channel is incompatible with permeability measurements. Early measurements were consistent with a single channel with a diameter of ~10 nm diameter,27 though a more recent results suggest a sieve-like barrier with a dominating mesh-diameter of ~5 nm.19 One possibility is that a relatively open central channel is gated at one or both ends by a constriction or a closed but porous structure (such as a hydrogel39,42,43,45,48), neither of which is likely to be directly detected by the reported SPEED experiments. Alternatively, the FG-network could permeate the entire central pore, but differences in FG-polypeptide composition, density and NTR loading could result in different translocation pathways. EM results in yeast, however, found no bias for GFP localizations, arguing against a central translocation conduit for small signal-independent cargos.111
Within the central pore, SPEED-generated spatial distribution models identify a peak Imp β1 density at a radius of ~23 nm (Figure 4),79,110 which corresponds to a location within a few nanometers of the scaffold wall. If the FG-network occludes most of the central pore, these data indicate that Imp β1 cargo traffic occurs near the NPC scaffold and the FG-polypeptide tether points, and likely not near the tips of the disordered polymers. In contrast, based on NTR binding affinities and the mobility of NTR-decorated beads on an FG-polypeptide monolayer, it was recently concluded that Imp β1 molecules are tightly bound along virtually the entire length of the FG-polypeptides, and that only Imp β1 interactions at the FG-network surface in the central channel are weak enough to allow for rapid NTR movement through the pore (Figure 5).55-57 This NTR-centric model explains how NTRs can be a critical element of the permeability barrier and how the free FG concentration can be reduced so that transiting NTRs bind to the FG-polypeptides with an affinity sufficiently low to enable fast movement. For the NTR-centric model to be consistent with the SPEED experiments, the cylindrical FG-network surface would have to have a diameter of ~40 nm, and thus, the central channel would enable passage of molecules with a diameter significantly larger than the size exclusion limit of ~4-5 nm.19 A potential solution to this dilemma is provided by the recent identification of two potential transport routes through the FG-network, as observed in cryo-electron tomography images of the central pore in native Xenopus NPCs. In addition to the commonly discussed central channel, peripheral channels were observed in a ring with a radius of ~23 nm (Figure 6).47 The conceptual implication is that the FG-polypeptides and NTRs can together form a structurally complex barrier with multiple translocation paths. Thus, the multiple transport paths postulated based on SPEED experiments can be reconciled with tightly-bound NTRs, assuming that these play an important role in creating the fine structure critical for a fully functioning NPC permeability barrier.
Figure 5. Kap-Centric (NTR-Centric) Model.
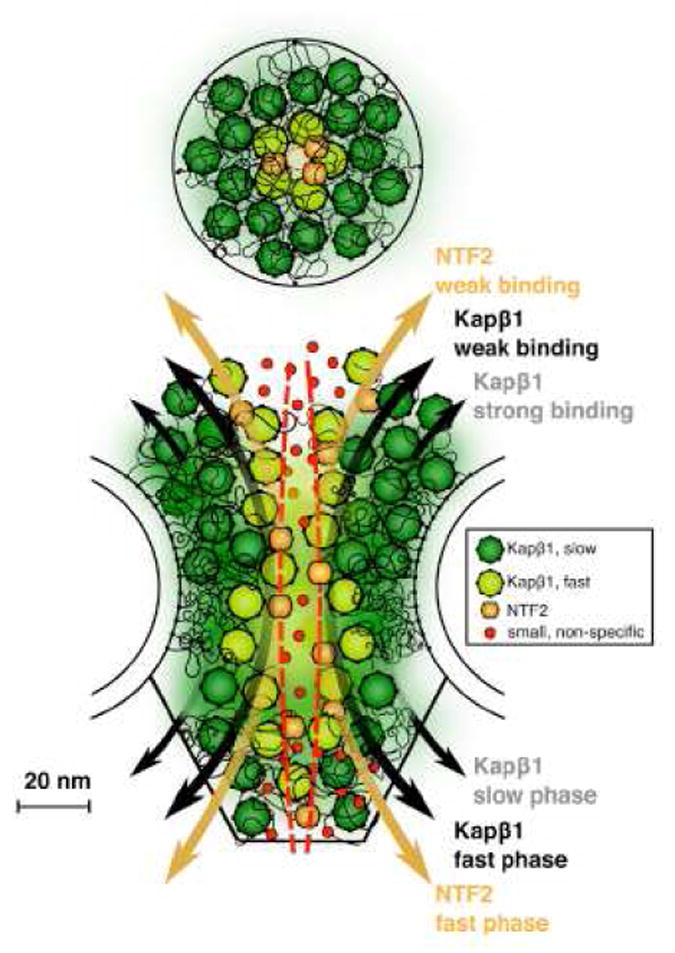
Strongly bound Imp β1 (Karyopherin β1; Kap β1) molecules occupy most of the FG-network region and are an integral constituent of the permeability barrier. When most of the FG binding sites are occupied, the Imp β1 affinity for the remaining sites is weak (low avidity), and therefore, the weakly-bound molecules can rapidly translocate through the pore. This model assumes that the weak affinity sites are centrally located, near the tips of the FG-polypeptides. Reproduced from reference 57.
Figure 6. Structural Elements within the NPC Central Pore.
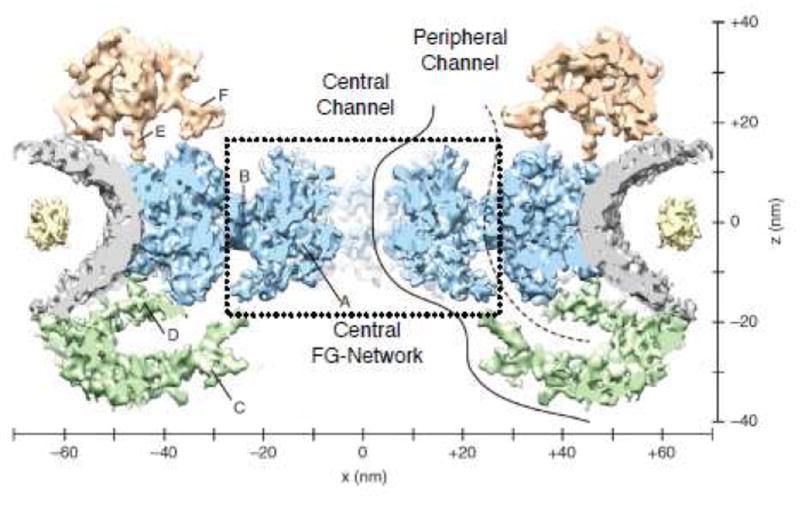
A 20 Å resolution map of the Xenopus laevis NPC showing elements of the FG-network, based on cryo-electron tomography. Gray, NE; blue, spoke ring (SR); green, nucleoplasmic ring (NPR); red, cytoplasmic ring (CPR); yellow, lumenal domains; solid, central conduit; dashed, peripheral conduit. The central channel ring (CCR) and SR-CCR interface are indicated as A & B, respectively. Extended linker structures are found in the nucleoplasmic ring (C & D) and in the cytoplasmic ring (E & F). Reproduced from reference 47 with minor modifications.
EXPORT OF mRNA CARGO
In the nucleus, eukaryotic mRNAs are packaged into ribonucleoprotein particles (mRNPs) and most are exported via diffusion through NPCs to the cytoplasm. Control of mRNA export is an important component of the regulation of gene expression.7 The extent to which mRNA export is regulated and the mechanisms underlying this regulation are poorly understood. Export of mRNAs is tightly linked to transcription and mRNA processing events, including capping, splicing, and polyadenlyation.112 For mRNA Pol II transcripts, presumably most, if not all, processing of the newly transcribed mRNA happens co-transcriptionally, thus influencing how mRNAs are packaged. The mRNA itself can have features that impact nuclear exit; for instance, the size of an mRNA directly impacts the transport pathway.113 Short mRNAs (200-300 nt) are exported by the U snRNP pathway, which uses CRM1 as an export factor, while longer transcripts likely predominantly use the NXF1-mediated mRNA export pathway.113 Recruitment of CRM1 to short mRNAs likely happens at the end of transcription elongation,114 whereas recruitment of NXF1 can occur cotranscriptionally and is mediated by formation of the TREX/TREX2 complex, thus providing a direct link between protein factor loading at the transcription site and the NPC.115,116
Single Molecule Characterization of mRNA Export
A first glimpse of the dynamics of mRNA export in live cells is now possible, due to creative labeling and sensitive detection strategies. Using RNA stem loop motifs, β-actin and dystrophin mRNAs were imaged during nuclear export in adherent mammalian cells.80,117 From EM work on BR2 export, a three-step process was predicted.118 In contrast, the export of β-actin mRNA was directly visualized as a four-stage process: the expected docking, translocation, and release steps, and an unexpected nucleoplasmic scanning step. For both β-actin and dystrophin mRNAs, translocation through the central pore was fast (< 20 ms). Nuclear docking and cytoplasmic release were significantly slower (~90 ms each for β-actin). Overall, complete transport of mRNAs including the docking and release steps was significantly slower than nuclear protein import, with initial average values reported as ~180 ms (β-actin) and ≤ 500 ms (dystrophin) with a range of individual translocation times from 40 ms to seconds.80,117 In more recent work in which a diverse random set of mRNAs was labeled, a wide range of NPC interaction times was found (from ~65 ms to ~6 s),119 in agreement with the initial reports. For mRNAs with interaction times in excess of 300 ms, the rate-limiting step of export was the nuclear docking step.119 In contrast, β-actin mRNPs spent a similar amount of time on the nucleoplasmic and cytoplasmic sides of the NPC.80 In contrast to this picture, more recent results from SPEED experiments yielded a total dwell time for β-actin and luciferase mRNPs of ~11-12 ms.120 SPEED-generated spatial distribution models for these mRNPs suggest that these particles translocate through the periphery of the central pore and they do not enter the central channel.120 In contrast, EM data reveal that the mRNA export factors Gle1 and Dbp5 are predominantly located in the central channel region.111 It is unclear if the conflicting results obtained using SPEED microscopy can be explained by the use of different cell lines and/or temperature.
Nucleoplasmic scanning, the unexpected fourth state in mRNA export, refers to high mobility behavior near the NE in which the mRNP appeared to interact with multiple NPCs prior to nuclear docking. During nucleoplasmic scanning, the β-actin mRNP had an average NPC interaction time of ~40 ms, which was shorter than the docking time for particles that ultimately were exported (~90 ms), but longer than expected for a particle freely diffusing. Thus, nucleoplasmic scanning and nuclear docking are distinct substeps of the export process. Nucleoplasmic scanning was observed in yeast for GLT1, CBL2 and MDN1 mRNPs, and the nuclear basket components Mlp1 and Mlp2 were found to promote scanning.121 Nucleoplasmic scanning was virtually absent for yeast GFA1 mRNPs after spheroblasting to remove the cell wall. Though GFA1 is involved in cell wall construction, it is unclear whether there is a connection between the lack of nucleoplasmic scanning and spheroblasting.122 Based on the observed behavior, scanning may reflect the availability of interaction sites for the different transport receptors or quality control mechanisms.
In 2D experiments, the distance from the mRNP to the NE during nucleoplasmic scanning was estimated as ≤ ~1 μm.123 Considering that the nucleus is a 3D object of irregular shape, 2D experiments could overestimate the average distance between the mRNA and the nearest NPC. This was confirmed by comparing the distances measured between mRNPs and the closest NPC in both 2D and 3D experiments. It was observed that more than 60% of mRNPs are found within 0.5 μm of an NPC in 3D experiments, whereas only 20% of mRNPs were found within this range of an NPC in 2D experiments.123 Interestingly, the number of mRNPs observed within 0.5 μm of the NE over 10 s is practically independent of the distance from the NE, indicating a relatively constant mRNP density within this region. Since the nuclear basket reaches only ~0.1 μm into the nucleoplasm,13,98 nucleoplasmic scanning does not occur by direct migration between core NPC proteins. One potential explanation for the diffusion space accessible for nucleoplasmic scanning is the chromatin exclusion zones near NPCs, which extend well beyond the expected NPC reach into the nucleoplasm. Tpr, a core part of the nuclear basket, appears to play a major role in generating these exclusion zones.124 Though clearly not fully understood at this point, nucleoplasmic scanning adds a novel, previously inaccessible, mRNA export component to gene regulation.
Cytoplasmic scanning was observed during GFA1 mRNA export, adding a fifth state to the export process at the NPC. In yeast, GFA1 mRNPs were highly mobile in a confined region for extended periods of time (up to 2 s) > 0.3 μm away from the NE on the cytoplasmic side after leaving the NPC through which they were exported. When the export factor Mex67p (NXF1 or Tap) was replaced with the temperature-sensitive mutant Mex67-5p at 26°C, cytoplasmic scanning occurred for as long as 7 s.122 Exclusion zones have also been observed on the cytoplasmic side of NPCs,125 suggesting that cytoplasmic scanning also results from confined diffusive motion.
Despite the wide range of cell types, labels and mRNAs that have been used, the general picture of the NXF1 mRNA export pathway from single molecule studies is relatively consistent. Namely, translocation through the central pore is rapid, and mRNP assembly and disassembly occur in the nucleoplasmic and cytoplasmic vestibules, respectively. These latter processes are significantly slower and mRNA-dependent. It remains unknown how quality control mechanisms and mRNA size and structure affect export. Nonetheless, a new window into the function of gene expression in the living cell has been opened.
Differences in NE Scanning by mRNPs
Considering that nucleoplasmic and cytoplasmic scanning are not always observed, and each is not observed for all mRNPs, it is intriguing to speculate whether mRNP scanning correlates with the function of the mRNAs. Nucleoplasmic scanning could be influenced by the transport state of the encountered NPCs (e.g., the presence of another cargo), a quality control mechanism, or a feedback mechanism that senses a localized need. In the case of β-actin, which is a housekeeping protein found throughout the cytoplasm, mRNA export is thought to be a continuously ongoing process in cells. However, cytoplasmic distributions of β-actin mRNPs can be polarized to the periphery or leading edge of a cell.126 At steady-state, β-actin mRNP interactions with the NE appeared random for ~40% of cells within a population (11 out of 27 cells), while for the remaining 60% of cells (16 out of 27 cells), interactions with only one half or even one quarter (5 of the 16 cells) of the NE perimeter were observed (Figure 7).80 These data suggest that β-actin mRNA export is controlled in response to a localized cytoplasmic need of the encoded protein. Nuclear scanning of NPCs by the mRNP could be one mechanism to correlate preferential localization of export events with the cytoplasmic localization of the mRNA. In contrast, as mentioned above, nucleoplasmic scanning was largely non-existent for yeast GFA1 mRNPs.122
Figure 7. Steady-state Distribution of β-actin mRNA in the Nucleus.
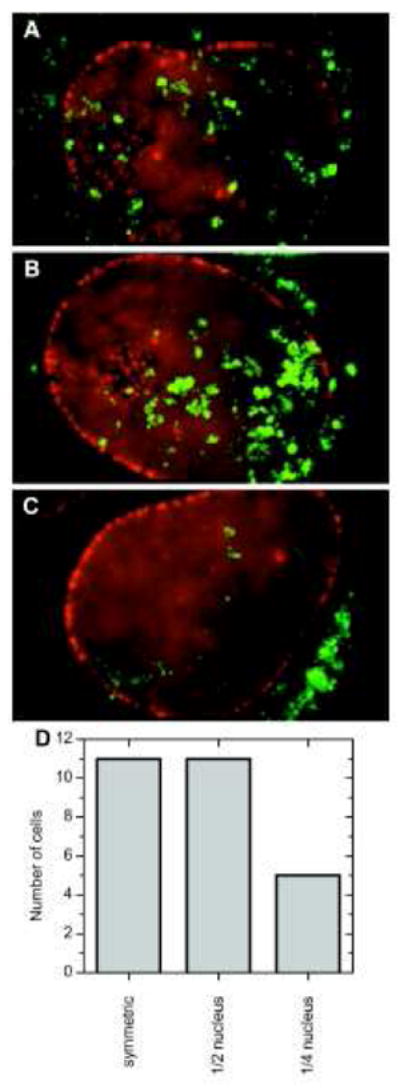
Interactions between β-actin mRNA (green) and the NE (red) were examined. The β-actin-24×MS2 mRNA was visualized with the stem loop binding protein MS2-YFP, and NPCs were tagged with tdTomato-Pom121. (A) Randomly distributed interactions between β-actin mRNA and the NE were observed for ~40% of cells. (B) For another ~40% of cells, such interactions were only found in one half of the nucleus. (C) For the remaining ~20% of cells, the mRNA interacts with a quarter or less of the NE. Modified from reference 80.
Cytoplasmic scanning is also observed for only some mRNPs. mRNPs of GFA1 (involved in cell wall synthesis) stay close to the cytoplasmic side of the NE and can move substantial distances (> 1 μm) along the NE.122 In contrast, scanning of the cytoplasmic face of the NE was not found for CLB2 (B-type cyclin), which is a DNA damage repair protein, and MDN1, which is linked to cell inheritance in yeast.121 It is unclear whether these differences in cytoplasmic scanning are related to the mRNA’s function.
Strategies for Labeling of mRNAs
Three principle methods for labeling mRNA in living cells – stem loops, hybridization probes and recombinant labeled proteins – have been used to fluorescently label and visualize single mRNA molecules. These labeling strategies require some comment, as there are advantages and valid concerns with all of them.
RNA stem loops like MS2 and PP7 are the most common labeling approach. RNA stem loops recruit specific protein binding partners, thus allowing RNA binding proteins genetically modified with fluorescent protein tags to be recruited to only one species of mRNA. The RNA binding proteins bind to stem loops with an affinity of ~1 nM. Stem loops are normally used in long (16 – 24x) repeats with a total size of ~1 kb.80 Multiple types of stem loops, e.g., MS2 and PP7, can be used simultaneously in the same cell.127-131 The influence of many added stem loops and their associated proteins on the mRNA export process is unclear. In addition, the spatial relationship between the tags and the mRNP-associated export factors required for NPC binding is unknown, thus introducing uncertainty into the meaning of the positional information. Yeast polyA mRNPs with RNA lengths ranging from about 0.5 to 6 kb are roughly cigar-shaped with a width of 5-7 nm and a length of 20-30 nm.132 Presumably, these mRNPs are most easily transported with their long axis aligned with the transport axis – the short axis is less than the diameter of the NPC’s putative central channel.132 The spherical Balbiani ring mRNP (~50 nm diameter) unfolds into a 7 nm diameter linearized structure for translocation through the NPC.133 Thus, stem loop tags could potentially be tens of nanometers away from mRNP-associated NPC binding proteins. The β-actin-24×MS2 mRNA is 3.3 kb, corresponding to an end-to-end length of ~20 nm for its mRNP.134 While the translocation channel (40-50 nm) is longer than most mRNPs, a conservative localization precision for most mRNP export studies of ~25 nm could lead to some serious localization errors, as recently discussed.122 Theoretical modeling indicates that tag position is important and while single and double end-tagged mRNAs report equally well on successful export events, a double end-tagged RNA is needed to correctly measure export efficiencies.135 A potential additional complication is the recent finding that stem loop tags can be cleaved from their mRNA in yeast.136 However, comparable data do not exist for mammalian cells.
A second type of labeling approach with single particle sensitivity is the use of dye-labeled hybridization probes that are target specific.137 Multiple approaches exist for which the fluorescence of the target bound form is much higher than that of the unbound form.138 Although not yet often used for single particle detection, development of this class of fluorescent labels is an active area.139-142 Delivery of these probes into the cell often calls for microinjection as bright membrane permeable versions do not yet exist. As for stem loops, the position and number of fluorescent hybridization probes within the mRNA are important. A primary concern is whether the tags affect any step of mRNA processing or mRNP transport, including any assembly and disassembly reactions occurring at the NPC. Whereas stem loop cassettes could interrupt unknown functional non-coding regions or structurally alter the mRNP, hybridization probes might bind to unknown regulatory domains or interfere with the recruitment of mRNP components.
The above issues with stem loops and hybridization probes are mitigated by a third method, microinjection of recombinant labeled mRNP-proteins, at the expense of losing the ability to target a specific mRNA species.119,137 The mRNA binding proteins hrp36 and DBP5 are assumed to randomly distribute along the entire length of the mRNP.119 Microinjected mRNP proteins are expected to occupy endogenous binding sites and mix with the endogenous population of the same protein factor, thus overcoming the ‘non-physiological’ concerns of stem loops and hybridization probes. Proper validation requires testing whether the microinjected and the endogenous factors have the same affinity and specificity. Differential mRNA binding interactions would result in over-/under-labeling, which could potentially introduce bias. Microinjection can potentially affect cell physiology (added components, volume change, and permeation stress), and these issues need to be examined. With regards to the amount of material microinjected, relatively few proteins are required for single molecule detection. Nonetheless, a substantial concentration jump is necessary to generate particles with a sufficient number of probes for detection over the background fluorescence from unbound, labeled and injected mRNP proteins. Particles that recruit a larger number of the probe proteins will be more likely to generate signals above the detection threshold but a high concentration of labeled probes will result in substantial out-of-focus fluorescence. Thus, the amount of injected material must be carefully calibrated.
Current work seeks to address the caveats mentioned in this section by developing new labeling strategies and improving existing ones. The newly developed Spinach and Broccoli hybridization probes are visualized using cell permeable dyes, but current versions of these dyes are unsuitable for imaging of individual RNAs due to multiplexing problems and poor brightness levels.143,144 Such cell permeable probes as well as CRISPR-Cas derived methods145,146 overcome the concerns inherent to microinjection. New dyes with optimal imaging properties are also being developed.147
STRUCTURAL STUDIES USING SUPER-RESOLUTION MICROSCOPY
Super-resolution fluorescence microscopy refers to any of a number of techniques designed to distinguish between two or more fluorescence particles located within the diffraction limit (which is ~200-300 nm for visible light), and/or to locate such particles with a precision better than this diffraction limit (see references 148 and 149 for reviews). The latter approach is exemplified by the 2D Gaussian fitting used for the sub-pixel resolution tracking of single proteins or mRNPs, the results of which were summarized in the previous sections. While NPCs are indeed very large, alternative super-resolution approaches are needed to determine the spatial relationship between multiple fluorescent molecules simultaneously present within an individual NPC. The fundamental problem is that multiple fluorophores spaced by less than the diffraction limit have overlapping fluorescence emission spots.148,149 In many cases, this problem is solved with one of multiple strategies that activate fluorescence emission from the different fluorophores at different points in time. Results from recent applications of super-resolution fluorescence microscopy approaches to NPC structural questions are described below.
Location of gp210 and the WGA Binding Sites
In dSTORM, fluorescent dyes are stochastically and individually photoactivated and then localized by 2D Gaussian fitting.150 Using dSTORM, the 8-fold rotational symmetry of the membrane anchoring protein gp210 was observed in Xenopus laevis NE’s in a 164 nm diameter ring (Figure 8A).151 Since the maximum outer diameter as visualized in EM images of a Xenopus NPC is ~125 nm (see Figure 6),16,47 the fluorophores apparently were located a significant distance away from the known NPC scaffold (by at least ~20 nm). One possibility is that the monoclonal antibodies, Fab fragments, and fluorophore tether combined to position the fluorophore fairly far from the antigenic region on gp210. Alternatively, it is possible that a protruding gp210 domain is not recovered in EM structures. The dSTORM approach also revealed that wheat germ agglutinin (WGA; a lectin that binds to O-linked GlcNAc moieties on the FG-polypeptides152,153) binds to NPCs in a doughnut-shaped distribution with a diameter of 41 nm (Figure 8B).151 It is unclear how WGA can inhibit both signal-dependent and -independent transport19,152 if it is located at the periphery of the central pore. In particular, how could WGA binding at the periphery of the ~50 nm pore block cargo translocation through the center of the pore? One possibility is that sample fixation interfered with reagent binding or caused structural modifications. Alternatively, it is possible that WGA binds within the peripheral conduits identified in recent EM images (Figure 6), and that a high WGA occupancy of these channels results in a structural change (e.g., swelling) that prevents translocation through a central channel. Since the superimposed averaged images in Figure 8C were generated from tens of thousands of individual localizations by directly imaging the plane of the NE from along the transport axis, these particle distribution clouds are expected to be more accurate than the 3D distribution models that can be generated by current SPEED analysis, for which only hundreds of values are typically collected within the central pore and a 3D image is generated from 2D side projections by assuming a model. However, the dSTORM images represent 3D distributions projected into 2D along the central axis, so different localizations along the transport axis cannot be resolved. Note that Löschberger and coworkers originally reported a spatial resolution of ~15 nm with 3500 collected photons per localization.151 In their more recent work, however, this resolution is reported as ~6 nm, which is likely more realistic given the number of photons collected (see later section on Biases and Errors).154
Figure 8. dSTORM Detection of gp210 and WGA in Fixed Nuclear Envelopes from Xenopus laevis Oocytes.
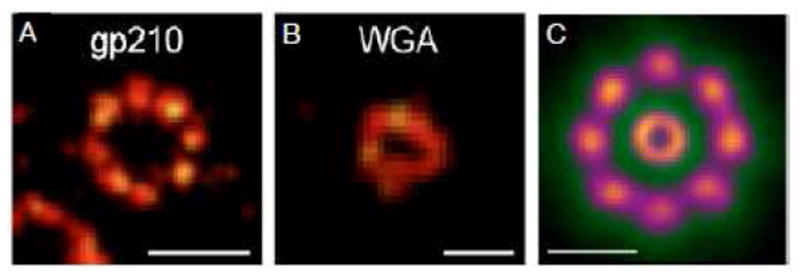
(A) NPCs tagged with monoclonal antibodies against gp210 and Alexa647-labeled Fab fragments. (B) NPCs tagged with WGA-Alexa647. (C) Superimposed averaged images of gp210 and WGA visualized structures. The 164±7 nm diameter gp210 ring was obtained from 426 individual rings containing ~160,000 localizations. The 41±7 nm diameter WGA ring was obtained from 621 rings containing ~40,000 localizations. Scale bars: 150 nm (A), 50 nm (B), and 100 nm (C).
Structural Composition & Variability
Because of the complexity of NPCs and the opportunity to regulate the diverse and massive amount of cargo traffic in both directions, a natural question is, are all NPCs the same? The answer seems to be no from both a functional and a structural standpoint. One form of structural diversity is variations in oligomerization state. For example, a small population of NPCs observed in dSTORM experiments (< 0.1%) had 9-fold rotational symmetry, instead of the normal 8-fold symmetry.154 This is consistent with previous EM studies, in which 9- and 10-fold symmetry were observed.155 In addition to these symmetry variations, individual polypeptide abundances vary within standard-symmetry NPCs. More precisely, using a proteomics approach, the relative abundance of about a quarter of NPC proteins was found to vary significantly (2- to 4-fold differences were common) between the NPCs in human cancer cell lines and five Nups showed variations across 44 tissue types and 30 disease states.156 To obtain absolute stoichiometries in these studies, photoactivated localization microscopy (PALM)157 was used to image NPCs and quantify the number of labeled proteins present. PALM is similar to dSTORM in that fluorophores are stochastically and individually photoactivated, the difference being the use of genetically-encoded photoactivatable fluorescent proteins rather than dyes. These PALM experiments revealed that > 90% of NPCs had over 16 copies of Nup107 (a wide distribution extending up to ~40 copies).156 Since fluorophore counting is complicated by blinking and inefficient fluorophore maturation (or premature photobleaching),158-160 Monte Carlo simulations were used to test various models, leading to the conclusion that there are 32 copies of Nup107 per NPC, an abundance which was essentially invariant over the different cell lines tested.156 In contrast, an inventory of 24 Nups in the yeast NPC by fluorescence intensity and stepwise photobleaching revealed that none of the examined proteins was present in more than 16 copies per NPC, including the yeast homolog of Nup107 (Nup84p).161 The aforementioned proteomics study identified ~32 copies of gp210 per NPC in HeLa cells,156 which contrasts with the 16 copies of gp210 per Xenopus NPC obtained with dSTORM experiments.154 Notably, gp210 varies significantly amongst different cell lines with close to 16 copies/NPC in RKO and SK-MEL-5 cells.156 These studies reveal the complexity of quantifying the oligomeric compositions of different NPCs, and indicate that variations can be expected between species, amongst different cell types, and even within a single nucleus. The functional implications of these differences have yet to be determined. Notably, however, mRNP tracking experiments revealed that some NPCs repeatedly exported mRNPs (up to 3 events in 5 s), whereas other NPCs were scanned, but were not observed to export any mRNPs, suggesting that not all NPCs may be simultaneously active in mRNA export.80 Whether these apparent functional differences are a consequence of variations in NPC structure or biochemically induced functional activities resulting from differences in bound material remains to be investigated.
The Y Complex
An atomic resolution structural model of the NPC scaffold is a major undertaking due to its large size, its rotationally symmetric but complex shape, and the large number of component polypeptides. A map of polypeptide positions has been generated computationally using experimentally determined constraints obtained with diverse methods.162,163 In addition, recent EM density maps of NPCs from different species have yielded a significantly improved picture of the architecture of the NPC (see von Appen & Beck Review in this JMB Special Issue). While an atomic model of the entire NPC is not yet available, multiple high-resolution structures for component polypeptides and oligomeric complexes are available (see Knockenhauer et al. Review in this JMB Special Issue). The Y complex is a major structural component of the NPC scaffold, the conserved core of which is comprised of six components.164 The orientation of the Y complex within NPCs was examined using ground state depletion (GSD) fluorescence microscopy.165 In GSD microscopy, fluorescent molecules near, but not at, the focus of an illuminating beam are photo-converted to a dark state, thus enabling selection of fluorophores actively emitting to those within a volume significantly smaller than a typical diffraction-limited beam waist.166 Using this approach, ring-shaped images were obtained for NPCs tagged at various positions on the Y complex with antibodies and nanobodies. From thousands of NPCs, the average radial distance of the fluorophore tags from the NPC center was determined with a precision of 0.1 nm and an accuracy of 0.3 nm. With such high resolution, it was argued that three different models of the orientation of the Y complex in the NPC could be ruled out.165 There is now convergence between single molecule, fluorescence anisotropy, EM, and crystallographic data to position the Y complex in a head-to-tail orientation on the cytoplasmic side, and perhaps also on the nucleoplasmic side. However, the exact positioning of the Y complex and whether there are one or two rings at each face of the pore remain open questions.47,164,165,167-169 Despite the high resolution of the GSD results, two rings of the Y complex could not be resolved, even if they do in fact exist (discussed later).
BIASES AND ERRORS IN PARTICLE LOCALIZATION MEASUREMENTS
Single molecule experiments have repeatedly demonstrated their ability to provide insight and information about biological processes that would be difficult or impossible to obtain by other approaches. Unfortunately, while single molecule experiments can be conceptually simple, the complexities and implications of the results can be difficult to fully understand due to numerous sources of error, which can lead to misrepresentations and misinterpretations. It is therefore important to discuss such sources of error in SMF experiments.
Particle Localization Error
Since light microscope images have pixel dimensions of tens to hundreds of nanometers and yet molecular positions that differ by nanometers can support substantially different molecular interpretations, the particle localization error is a major concern for the SMF microscopist. Multiple particle localization algorithms exist and fitting the pixelated emission pattern from a CCD camera to a 2D Gaussian was initially determined to be the best approach for determining the position of point sources to sub-pixel precision, particularly at low signal-to-noise ratios.77 This is the approach used for most of the single molecule particle tracking data discussed in this review. The maximum likelihood estimator actually yields a better precision under some conditions that more closely approximates the Cramér-Rao lower bound (CRLB), which is the theoretical limit based on the Fisher information matrix.170-172 The maximum likelihood estimator has not been generally adopted by the NPC field, though it was used to evaluate mRNA tracking in yeast.122,173 The first model for the localization error using a 2D Gaussian fit was estimated by Thompson et al.78 as:
| σg=s2+a2/12N+8πb2s4a2N2 | (1) |
|---|
where σg is the error in each of the two dimensions defined by the CCD array, s is the standard deviation of the Gaussian fit, a is the effective pixel dimension, b is the background noise (in photons per pixel), and N is the total number of photons collected in the spot. Note that for a sufficiently low background, the error scales approximately with the square root of N. A more rigorous mathematical derivation yields:171
| σg=F[(43)2s2+a2/12N+8πb2(s2+a2/12)2a2N2] | (2) |
|---|
where F is 1 for a CCD or CMOS detector and 2 for an electron multiplying CCD (EMCCD).171,174,175 While these derivations assume a static (immobile) particle, the blurring (spot broadening) expected for a mobile particle is accounted for as follows:176
| s2=s02+Dt3+λ248π2n2s02(Dt+zlim2) | (3) |
|---|
where s0 is the Gaussian standard deviation in the focal plane, D is the diffusion constant of the particle, t is the image integration time, λ is the emission wavelength, n is the refractive index of the medium, and ±zlim are the optical axis boundaries in which the average particle position must be during image acquisition to remain detectable. Since the fluorescence emission pattern is no longer expected to be symmetric due to the particle’s movement, the centroid localization precision, σc, is a better estimate of the error:176
| σc=F[s2+a2/12N+(92)2πb2(s2+a2/12)2a2N2] | (4) |
|---|
Note that Eq. 3 was derived to be used with Eq. 4.
The particle localization precision can be determined experimentally for static particles (e.g., molecules attached to a coverslip surface) by repeatedly measuring the position of the particle. The standard deviation of these measurements is defined as the precision.74 Based on this approach, Eq. 1 underestimates the precision by ~30%, which is corrected by the 4/3 factor in Eq. 2.78,171 According to Eqs. 2 and 4, the precision is worse for EMCCD cameras by a factor of 2 due to the noise from the electronic multiplication gain (accounted for by F = 2; but see Figure 9).175 Particle diffusion introduces additional error, which depends both on the diffusion constant and the integration time. For zlim2 ≈ 0 (i.e., the average position of the diffusing particle is near the focal plane), particle diffusion becomes relevant when Dt ≥ ~0.005 μm2. As D values within the NPC are typically ~1-10 μm2/s,58 integration times < ~1 ms are usually sufficient to reduce the error due to particle motion to a negligible level. These error estimation models are graphically illustrated for different N values in Figure 9A. Importantly, Eqs. 1-4 do not account for readout noise, and hence are really only valid for high photon counts (N = thousands). Calculations including readout noise and electronic multiplication gain indicate that the Mortensen formula with F = 2 (Eq. 2) OVERestimates the localization error for EMCCD cameras at low N. In contrast, the Mortensen formula with F = 1 UNDERestimates the localization error for CCD and CMOS cameras at low N (Figure 9B).
Figure 9. Localization Error.
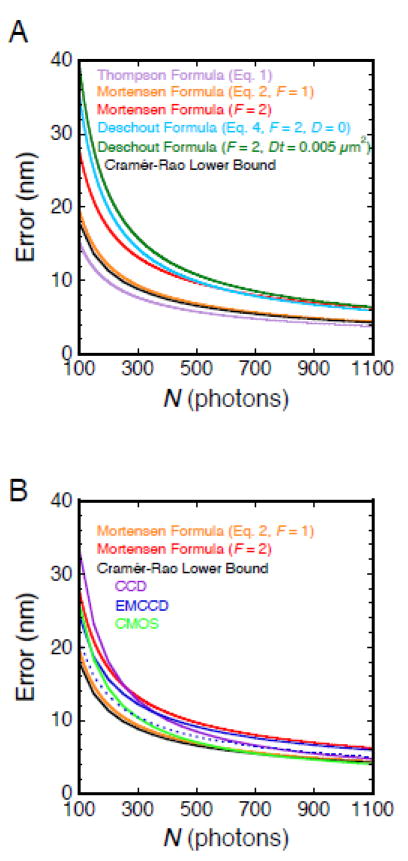
(A) Different localization error estimators. The Cramér-Rao lower bound (CRLB) is the fundamental limit of localization precision based on the Fisher information matrix, and was calculated using the FandPLimitTool (http://www.wardoberlab.com/software/fandplimittool/).170,172,201,202 The CRLB shown here (black) was calculated for an Airy profile and does not include any readout noise, as this is not accounted for in any of the localization error estimators. The commonly used Thompson formula (Eq. 1; lavender), which estimates the localization error when fitting the point spread function with a 2D Gaussian, underestimates the CRLB, and is therefore an unsuitable approximation. The Mortensen formula (Eq. 2) is a more accurate approximation of the localization error, and more closely matches the CRLB when F = 1 (orange). The Mortensen formula with F = 2 (red) accounts for the electronic multiplication gain error inherent in EMCCD cameras. The Deschout formula (Eq. 4; light blue; Dt = 0, s0 ≈ 100 nm, _zlim_2 = 0, n = 1.33, λ = 670 nm) estimates the localization error for the centroid of the emission pattern from a moving particle, and closely approximates the Mortensen formula at higher N values. The localization error due to particle movement is larger than the static precision when Dt > ~0.005 μm2 (dark green; Dt = 0.005 μm2). Parameters (unless otherwise noted): NA = 1.45, magnification = 100X, λ = 690 nm, s = 100 nm, a = 240 nm, and b = 4.5 photons/pixel. (B) Localization errors for different types of cameras. The localization errors using different imaging modes were calculated with the approach used for the CRLB in (A) with the following parameters, which are typical for modern cameras: CCD (purple, a = 130 nm, readout noise = 6 e-/pixel); EMCCD (dark blue solid, a = 240 nm, readout noise = 46 e-/pixel, EM gain = 950); CMOS (green, a = 65 nm, readout noise = 1.5 e-/pixel). While the CCD and CMOS results approach the Mortensen formula curve for F = 1 at high N, as expected, divergence occurs at low N values, emphasizing the need to account for readout noise. Also as expected, the EMCCD results approach the Mortensen formula curve for F = 2 at high N. However, at low N, the Mortensen formula curve substantially deviates from the EMCCD results since the F = 2 value is not valid in the low photon count region, according to rigorous mathematical modeling that accounts for the EM gain and readout noise of an EMCCD detector.201 The CMOS imaging mode outperforms the EMCCD in most cases, though not accounted for here is the lower quantum efficiency of CMOS detectors (~20-25% less). An EMCCD with 160 nm pixels and readout noise = 65 e-/pixel (dark blue dashed) yields a substantial improvement compared with 240 nm pixels. In all cases, the model pixel array approximates a similar region of interest (approximately 1.2 μm × 1.2 μm).
Reference, Registration and System Stability Errors
In order to properly interpret particle distribution maps of molecules interacting with NPCs, there are additional errors that must be accounted for. In addition to the particle localization error, there is an error associated with the localization of the reference point, e.g., a labeled Nup (σNPC). If the NE, rather than an individual NPC, is used as a reference, trajectories are typically assumed to pass though the center of the pore, which is often unlikely to be true (e.g., Imp β binding to the periphery of the central pore – see Figure 4), giving rise to a lateral localization error (σNE-l) in addition to the NE localization error (σNE-a), which is perpendicular (axial) to the NE plane. These errors introduce broadening in particle distribution maps (such as those shown in Figures 1, 3A & 4B). Different optical paths and wavelengths imply an image registration error (σR) that must be accounted for in precision work, regardless of whether the same or different cameras are used for the transiting particle and NPC/NE images. Stability of the image (σi), which is influenced by microscope stage drift and/or movement of the reference (e.g., the NE or the NPC), also contributes to the overall error. Fortunately, σi is typically small (< ~1 nm/s) for single molecule NPC studies in permeabilized cells,73,103 and simultaneous tracking of reference and particle can be used to minimize σi under live conditions where long-term stability is more problematic.79,80
The Total Error and Its Importance for Interpreting SMF Images
The distinct and independent errors described in the previous sections need to be combined to obtain the total error. We will use the SPEED approach to provide an example since the total error is critical to interpreting the data from these experiments. The σR is reported as ~3 nm,120 similar to what was found by others.87,99,177 The σi is not reported for SPEED, presumably since NPC and single particle positions are alternately and continuously acquired.79 The σNPC is reported as ~1-2.5 nm in permeabilized cells,79 and 5-11 nm in live cells.120 The former value appears to be an underestimate, as the error predictors discussed earlier (Figure 9) indicate that N well in excess of 5000 photons is required to achieve this error level (not shown). Consequently, σNPC is likely no better than ~4-6 nm in permeabilized cells. The higher σNPC value reported for live cells is explained by higher NPC mobility under these conditions (i.e., implying an increase in σi),120 though presumably continuous NPC tracking should minimize the effects of sample movement. Since only well-isolated NPCs exhibiting 8 photobleaching substeps are assumed to have been selected for analysis,120 the error due to incomplete/inhomogeneous labeling of the NPCs (σL) is considered insignificant. Consequently, assuming σg = 10 nm as reported,79,110 the total error in SPEED experiments can then be estimated from σ = (σg2 + σNPC2 + σR2)1/2 as ~11 nm in permeabilized cells. However, it is unclear how σg was calculated from Eq. 1 as described,79 since, using the parameters provided, the Thompson formula (used by the authors)78 yields σg ≈ 4 nm. Instead, recalling that Eq. 1 significantly underestimates the localization error (Figure 9) and assuming N = 1100 photons as reported,79 Figure 9 indicates that σg ≈ 6 nm (Mortensen, F = 2), which yields σ ≈ 8 nm (better than the 11 nm calculated from the authors’ numbers).
In most SMF experiments, a low total localization error is implicitly required to draw meaningful conclusions, i.e., if differences between conditions are observed, the error must be sufficiently low to observe the differences. However, a more explicit analysis of the effects of error is required when testing the data against a model, or for more refined interpretations of particle distribution maps. To demonstrate the role of error in distinguishing a tube-shaped distribution from a center-filled distribution for Imp β1 as determined by SPEED experiments (Figures 4E & 4F), simulations were performed using the following model. Particles were assumed to be randomly positioned on the surface of a 50 nm long cylinder with a radius of 23 nm. These values correspond to the length of the NPC central pore and the location of the peak Imp β1 intensity obtained from SPEED analysis.79 We then determined how this cylindrical particle distribution would look if examined from the side in SMF experiments over a range of particle localization precisions. As the total error, σ, is increased from 5 nm to 20 nm, the two peaks diagnostic for a tube-shaped distribution merge into a single peak in the particle distribution histogram, with a transition point around 8-10 nm (Figure 10A). A thicker (and more realistic) Imp β1 interaction volume would further broaden peaks, requiring even greater localization precision. As discussed in the previous paragraph, the total error in SPEED experiments is ~8-11 nm.110 Notably, the ability to distinguish the presence of one or two peaks in the particle distribution histogram also depends on N. For example, assuming σ = 10, two independent distributions obtained for N = 10,000 are similar, whereas N = 200 datasets (approximate size of central pore datasets in current SPEED analysis79,110) vary significantly (Figure 10B). This analysis suggests that most current SPEED datasets are likely undersampled.
Figure 10. Noise Level Required to Detect a Tube-shaped Particle Distribution in NPCs.
(A) Simulations assuming different noise levels. 10,000 particle positions were randomly selected on the surface of a cylinder with length 50 nm and radius 23 nm, a simple model of the 3D spatial distribution for Imp β1 in the central channel of the NPC according to Figure 4. Noise in the 3D position measurements was added based on the selected noise level (σ), i.e., normally distributed random error in position. Errors in x and y were assumed to be equal. An error in z is not included because it does not affect the position measurement in the _xy_-plane. The coordinate system of Figure 4 was used. Note that distinguishing one peak from two in the particle density histograms requires low error (the error per bin can be roughly approximated as the square root of the number of measurements in the bin). (B) Examples of particle density histograms obtained under undersampling conditions (low N). (top panel) The simulation in (A) was repeated for σ = 10 (N = 10,000). This histogram is similar to that obtained in row 3 of (A), indicating sufficient sampling. (lower panels) The lower 5 histograms show N = 200 groups of data (similar to N in Fig. 4B) from the simulation in the top panel. It appears impossible to draw conclusions from one of these panels, none of which resembles the parent distribution.
Bias due to Pixel Size
Besides the measurement errors discussed in the previous sections, SMF data are also prone to bias. The term ‘bias’ is used, rather than ‘error,’ to differentiate between factors influencing accuracy (bias or systematic error) from those affecting precision (random error). Accuracy reflects how close the true position is to the experimental average position whereas precision refers to the variation in repeated measurements.
Equations 1, 2 and 4 were derived assuming that a ≤ σ.78,171,176 This condition is typically not satisfied in SMF experiments on NPCs as pixel sizes – in image space – are often ~240 or ~160 nm whereas σ is ~100 nm (all pixels are assumed to be square, so only one dimension is given). Using the typical 2D Gaussian fitting algorithm, the consequences of violating the above assumption can be severe for 240 nm pixels, depending on the position of the particle relative to the pixel center. The fitting bias appears substantially smaller for 160 nm pixels.178 The problem arises from the method by which the expectation value for a given pixel is determined. The traditional approach is that the value of the 2D Gaussian at the center of the pixel is a reasonable approximation for the average value of this model integrated across the pixel. This is, not surprisingly, a reasonable assumption for small pixels, but not for large ones. The bias in a single _x_- or _y_-dimension can be > 15 nm for pixels of ~250 nm.178 At this time, it is unclear what the average bias is, as the bias was only estimated for the particle located at a few positions relative to a pixel’s center.178 Importantly, however, a solution was provided, namely that a more accurate estimation of the expectation value for the collected photons according to the 2D Gaussian model would improve the accuracy to < 1 nm.178
Bias Due to Rotational Immobility
With the report of sub-nanometer precision in SMF microscopy experiments on NPCs151,154,165 and the continuous improvement of instruments to address various questions, a word of caution is advisable regarding rotational mobility, which is not generally considered in SMF experiments. Single particle positions are typically determined by fitting the observed fluorescence intensity distribution to a 2D Gaussian. Since the direction of fluorescence emission is dependent on dipole orientation, an implicit assumption in single molecule experiments is that the molecule of interest is able to freely rotate. In many cases, this is reasonable. However, isotropic molecular rotation can be hindered in dense structures, by tethering, by high local viscosity, and/or by non-covalent interactions (e.g., a dye sticking to the surface of a protein). If molecular rotation is not averaged over the integration time, the center of the fluorescence intensity distribution may no longer be a suitably accurate measure of the particle’s position, as the point spread function becomes asymmetric.179,180 For slow molecular rotation (e.g., a fixed particle), a bias of up to 40 nm is possible, although a moderate bias (< ~10 nm) is more typical, but nonetheless significant, for mobile but oriented molecules.181-183 The bias can be substantial (> 100 nm) for out-of-focus, oriented molecules (≥ 300 nm from the focal plane).184 The orientation of the transition dipole relative to the optical axis determines the direction of the bias. Importantly, use of an azimuthal polarization filter eliminates bias due to both rotational immobility and out-of focus emission, but the reduced collection efficiency results in a worse localization precision (by ~30-75%).185
What does Current Single Molecule Data on NPCs Really Tell Us?
The above discussion on biases and errors can certainly raise concerns about the confidence a reader should place on the results reported in studies of nucleocytoplasmic transport using SMF approaches. We therefore summarize where we expect that results would be minimally affected by any necessary corrections, and areas where current results are not so definitive.
SMF experiments investigating various aspects of nucleocytoplasmic transport are typically analyzed and reported as single molecule localizations or trajectories overlaid onto an NPC scaffold or the NE (e.g., Figures 1 and 3). Since numerous NPCs are typically analyzed, the average bias is likely ~0, and thus biases effectively increase the width of particle distributions, but do not influence the average position. Therefore, the consequences of both the errors and biases described earlier are broader distributions of single molecule spots.27,110 Though particle distributions may be broadened, it is often the centers of such distributions that are the relevant outcome of the experiment. For example, assigning a particular particle average to one of the vestibules or to the central pore is likely generally reliable (such as the region for the appearance/disappearance of smFRET in Figure 1), though reliability does depend on distance from a transition zone since individual particle localizations near a transition zone cannot be reliably assigned to one region or another. In contrast, distribution broadening could explain, at least in part, why the central passageway for signal-independent cargos is found to be ~18 nm in SPEED experiments,110 compared with ~5-10 nm from permeability measurements.19,27 Since NPC-bound molecules move significantly slower than freely diffusing molecules, average interaction times are likely fairly reliable, though photobleaching, blinking, and sufficient movement from the focal plane would all result in reduced individual interaction times.
The error of individual measurements plays a critical role in distinguishing between two different populations of single molecules. An illustrative example is the GSD microscopy approach discussed earlier for examining the orientation of the Y complex.165 While a precision of 0.1 nm in the GSD experiments suggests that the presence of multiple rings of the Y complex with radii that differ by a few nanometers should be readily resolvable, this is actually not possible with the approach used. The precision of 0.1 nm refers to the error in the average radius (standard error of the mean) of the ring-shaped fluorescence distributions from various labeled Y complexes. The reason that this number is so low is because of the high number of single particle measurements (in the high thousands). In contrast, the precision with which an individual fluorophore is located in these experiments is ~30 nm, which implies that it is not possible to place individually detected events into separate bins representing two distinct rings that differ in radius by only a few nanometers. The individual fluorophore localization precision is independent of the number of measurements. This message applies to dSTORM, PALM and particle tracking experiments as well, namely that the error in the average position can be substantially minimized with high N values, although the individual measurement error is unaffected. These limitations suggest that it is likely to be impossible to determine the presence of two Y complex rings using averaged positional information (which includes added tags) unless the precision can be substantially improved. Such an analysis would be even more complex if there were different double-ring Y complexes on the cytoplasmic and nucleoplasmic faces of the NPC.47,164,168,169
Measurement error also influences the ability to characterize the shape of a distribution comprised of only a single type of particle. For example, the simulations in Figure 10 illustrate the role of measurement error in SPEED analysis. Importantly, however, comparison of SPEED generated particle distribution maps for signal-independent and -dependent particles (the raw 2D data rather than computer-generated 3D maps) reveals clear differences in widths at the NPC central pore,79,110,120,186 implying that the two transport pathways use different parts of the FG-network. That is, signal-independent cargos access a significantly smaller region within the central pore, consistent with the central channel hypothesis. The pathway for signal-dependent cargos is less certain since additional possible models have not been tested. Moreover, as discussed earlier, the total error in current SPEED data is unclear and the distributions are undersampled. Thus, whether signal-dependent cargos are confined to the periphery of the pore, to distinct peripheral channels, or whether they access a central channel to some extent remains an open question. In addition, the significance and magnitude of differences in widths of the central channel at different Imp β1 concentrations110 remains uncertain. Simulations incorporating the experimental conditions and analysis algorithms would significantly strengthen interpretations and provide insight to direct future experiments. Nonetheless, the conceptual problems that the SPEED approach has been applied to are important, and the basic concept that back projected transforms of 2D experimental data can be tested against the predictions of a 3D model is powerful.
SUMMARY AND CHALLENGES FOR THE FUTURE
Single molecule approaches can answer many structural and functional questions about nucleocytoplasmic transport. Despite major improvements in methods and instrumentation and the richly satisfying images and videos that can be recorded, these data nonetheless still require careful interpretation and analysis. For example, the errors inherent within recordings of particle localizations are typically underappreciated, and are generally not summarized in a concise manner. This can lead to overanalysis. On the other hand, due to the diffraction limit, a stationary particle will yield a Gaussian-like distribution of localizations, implying that the real spatial distribution of stationary and moving particles may be substantially smaller than an image portrays. Simulations in which particle distribution models are tested by including experimental parameters and noise values will lead to a better understanding of how stochasticity influences the system being probed and the ability of the resultant experimental data to distinguish between various models. In addition, the 3D nature of nuclear transport is often simplified when trying to communicate single molecule data, and this can unfortunately lead to misleading images and inaccurate interpretation. For example, the central pore is ~50 nm in diameter, and yet particles in the vestibules could potentially be found in a range of ~100 nm along the optical axis. Thus, for similar binding affinities, approximately twice as many particles should be observed in the vestibule regions. This contrast is magnified if the entire central pore is not available for binding, which is likely the case. Consequently, it is uncertain if the two peaks observed in Figure 3B arise due to a higher affinity for Imp β1 in the vestibule regions or because the accessible volume and number of binding sites is substantially higher.
While only a handful of labs were able to execute early single molecule experiments, numerous fluorescence microscopy approaches are now more readily available to the wider research community. Nonetheless, the 3D nature of the cell does present challenges for interpreting 2D images, raising the need for real-time 3D imaging. True 3D information can be obtained using several strategies, including using astigmatism, double-helix and corkscrew engineering of the point spread function (PSF) as well as by multiplane imaging.187-190 Similar to the double-helix and corkscrew approaches, multi-focus-microscopy (MFM) uses Fourier engineering of the PSF but records classical images rather than transformed PSFs encoding the _z_-information.191 The alignment of MFM data is challenging but can be accomplished by using 3D single molecule real-time (SMRT) microscopy with internal registration markers.123 All these 3D techniques use lower excitation power than SPEED microscopy, but have worse time resolution. These methods demonstrate the potential for advances in image analysis and processing. Finally, similar to the way Fourier ring correlation was introduced as a direct measure of resolution in super-resolution microscopy,192 it would be beneficial if user-dependent signal selection could be replaced by defined (automated) particle analysis algorithms. One step in this direction is a generalized likelihood ratio test method for signal detection in raw images.193
While traditional approaches (e.g., X-ray, NMR and EM) are expected to dominate structural studies of the scaffold proteins, single molecule methods can certainly help resolve specific structural questions, especially if stochastic imaging modalities can be pushed into cryogenic temperature regimes. The use of nanobodies and short tethers will reduce error caused by distance from the epitope.194 Where SMF methods will really shine, however, is in understanding structural and functional aspects of the FG-network. Combining such approaches with theoretical modeling and analyses is expected to be particularly powerful as the dynamic and stochastic nature of the FG-network and cargo transport can be directly modeled and tested. Super-resolution fluorescence microscopy methods are expected to help resolve the dynamics and spatial distribution of the FG-polypeptides, the extent to which NTRs penetrate the FG-network vs. interact with its surface, and the role(s) of NTRs in defining the characteristics of the permeability barrier. While it is certainly likely and expected that import and export cargos (both proteins and mRNAs) transit through a central channel,195 perhaps simultaneously, it is unclear to what extent the pathways overlap and modulate each other. It seems inevitable that high concentrations of import and export cargos that both use the same translocation conduit would lead to jamming of the pore. Separate import and export conduits through the FG-network, as supported by recent EM data, seems more likely, but requires additional experimental support. It remains unknown how massive cargos that occupy much of the central pore during transit (e.g., QDs, ribosomal subunits or viruses) are able to temporarily displace the FG-polypeptides and any bound NTRs in order to penetrate the permeability barrier. The long residence times of such cargos are likely to significantly perturb the steady-state distribution of NTRs, impede the translocation of both import and export cargos, and modulate the local RanGTP gradient. Such effects could even temporarily bias the direction of transport, and thus, on an instantaneous level, NPCs are likely to have different functional activities by stochastically switching from a net import mode to a net export mode depending on the recent history of transported cargos.196 Even in the case of smaller cargos, can cargos condition NPCs, i.e., make the transport of similar cargo more or less likely, at least briefly?
While some structural and functional differences in NPCs have been detected and some can be strongly argued to exist, as discussed above, it is critical to establish the biological implications of such differences. An important question in this regard is whether and what biochemical mechanisms spatially and differentially regulate NPC activity by changes in NPC properties, and to distinguish such modulations from stochastic variability, or spatial variations in subcellular localization. There is evidence that mRNA export is differentially regulated,197 though it is unclear whether mRNA exporting NPCs transport all mRNAs, or whether they are pathway specific or otherwise regulated, e.g. in response to cell polarization or development, as has been suggested.198,199 For some proteins, nuclear import is enhanced by microtubule trafficking, presumably by cargo unloading near a subset of NPCs.200 Single molecule imaging is poised to play a major role in addressing these questions and in clarifying the role of NPCs as autonomous transporters versus their local influences on the quality control of transport complex assembly and maturation, and their broader influences on other cellular processes, such as transcription and intracellular trafficking.
HIGHLIGHTS.
- Nuclear pores mediate macromolecular exchange between the nucleus and cytoplasm.
- A network of intrinsically disordered polypeptides forms the permeability barrier.
- Single molecule fluorescence approaches have enabled biophysical characterization.
- Transport complex assembly and disassembly occurs in vestibules at the pore exits.
- Future single molecule studies are needed to resolve numerous outstanding problems.
Acknowledgments
We thank Thomas Schwartz, Guo Fu, and Darryl Conte for discussions and proofreading, and Amir Tahmasbi, Jerry Chao, and Raimund Ober for assistance with Figure 9 and the section on biases and errors. This work was supported by the Welch Foundation (BE-1541, SMM).
Abbreviations
NPC
nuclear pore complex
NE
nuclear envelope
SMF
single molecule fluorescence
Nup
nucleoporin
NTR
nuclear transport receptor
NLS
nuclear localization signal
smFRET
single molecule fluorescence resonance energy transfer
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Jokhi V, Ashley J, Nunnari J, Noma A, Ito N, Wakabayashi-Ito N, Moore MJ, Budnik V. Torsin mediates primary envelopment of large ribonucleoprotein granules at the nuclear envelope. Cell Rep. 2013;3:988–95. doi: 10.1016/j.celrep.2013.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Speese SD, Ashley J, Jokhi V, Nunnari J, Barria R, Li Y, Ataman B, Koon A, Chang YT, Li Q, Moore MJ, Budnik V. Nuclear envelope budding enables large ribonucleoprotein particle export during synaptic Wnt signaling. Cell. 2012;149:832–46. doi: 10.1016/j.cell.2012.03.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Tu L-C, Musser SM. Single molecule studies of nucleocytoplasmic transport. Biochim Biophys Acta - Mol Cell Res g. 2010;1813:1607–18. doi: 10.1016/j.bbamcr.2010.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Stewart M. Molecular mechanism of the nuclear protein import cycle. Nat Rev Mol Cell Biol. 2007;8:195–208. doi: 10.1038/nrm2114. [DOI] [PubMed] [Google Scholar]
- 5.Grossman E, Medalia O, Zwerger M. Functional architecture of the nuclear pore complex. Annu Rev Biophys. 2012;41:557–84. doi: 10.1146/annurev-biophys-050511-102328. [DOI] [PubMed] [Google Scholar]
- 6.Raices M, D’Angelo MA. Nuclear pore complex composition: a new regulator of tissue-specific and developmental function. Nat Rev Mol Cell Biol. 2012;13:687–99. doi: 10.1038/nrm3461. [DOI] [PubMed] [Google Scholar]
- 7.Rodriguez-Navarro S, Hurt E. Linking gene regulation to mRNA production and export. Curr Opin Cell Biol. 2011;23:302–9. doi: 10.1016/j.ceb.2010.12.002. [DOI] [PubMed] [Google Scholar]
- 8.Hetzer MW, Wente SR. Border control at the nucleus: biogenesis and organization of the nuclear membrane and pore complexes. Dev Cell. 2009;17:606–16. doi: 10.1016/j.devcel.2009.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rout MP, Aitchison JD. The nuclear pore complex as a transport machine. J Biol Chem. 2001;276:16593–6. doi: 10.1074/jbc.R100015200. [DOI] [PubMed] [Google Scholar]
- 10.Fahrenkrog B, Aebi U. The nuclear pore complex: nucleocytoplasmic transport and beyond. Nat Rev Mol Cell Biol. 2003;4:757–66. doi: 10.1038/nrm1230. [DOI] [PubMed] [Google Scholar]
- 11.Cronshaw JM, Krutchinsky AN, Zhang W, Chait BT, Matunis MJ. Proteomic analysis of the mammalian nuclear pore complex. J Cell Biol. 2002;158:915–27. doi: 10.1083/jcb.200206106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Stoffler D, Feja B, Fahrenkrog B, Walz J, Typke D, Aebi U. Cryo-electron tomography provides novel insights into nuclear pore architecture: implications for nucleocytoplasmic transport. J Mol Biol. 2003;328:119–30. doi: 10.1016/s0022-2836(03)00266-3. [DOI] [PubMed] [Google Scholar]
- 13.Beck M, Förster F, Ecke M, Plitzko JM, Melchior F, Gerisch G, Baumeister W, Medalia O. Nuclear pore complex structure and dynamics revealed by cryoelectron tomography. Science. 2004;306:1387–90. doi: 10.1126/science.1104808. [DOI] [PubMed] [Google Scholar]
- 14.Kiseleva E, Allen TD, Rutherford S, Bucci M, Wente SR, Goldberg MW. Yeast nuclear pore complexes have a cytoplasmic ring and internal filaments. J Struct Biol. 2004;145:272–88. doi: 10.1016/j.jsb.2003.11.010. [DOI] [PubMed] [Google Scholar]
- 15.Maimon T, Elad N, Dahan I, Medalia O. The human nuclear pore complex as revealed by cryo-electron tomography. Structure. 2012;20:998–1006. doi: 10.1016/j.str.2012.03.025. [DOI] [PubMed] [Google Scholar]
- 16.Frenkiel-Krispin D, Maco B, Aebi U, Medalia O. Structural analysis of a metazoan nuclear pore complex reveals a fused concentric ring architecture. J Mol Biol. 2010;395:578–86. doi: 10.1016/j.jmb.2009.11.010. [DOI] [PubMed] [Google Scholar]
- 17.Yang Q, Rout MP, Akey CW. Three-dimensional architecture of the isolated yeast nuclear pore complex: functional and evolutionary implications. Mol Cell. 1998;1:223–34. doi: 10.1016/s1097-2765(00)80023-4. [DOI] [PubMed] [Google Scholar]
- 18.Görlich D, Kutay U. Transport between the cell nucleus and the cytoplasm. Annu Rev Cell Dev Biol. 1999;15:607–60. doi: 10.1146/annurev.cellbio.15.1.607. [DOI] [PubMed] [Google Scholar]
- 19.Mohr D, Frey S, Fischer T, Güttler T, Görlich D. Characterization of the passive permeability barrier of nuclear pore complexes. EMBO J. 2009;28:2541–53. doi: 10.1038/emboj.2009.200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Peleg O, Lim RY. Converging on the function of intrinsically disordered nucleoporins in the nuclear pore complex. Biol Chem. 2010;391:719–30. doi: 10.1515/BC.2010.092. [DOI] [PubMed] [Google Scholar]
- 21.Lim RYH, Ullman KS, Fahrenkrog B. Biology and biophysics of the nuclear pore complex and its components. Int Rev Cell Mol Biol. 2008;267:299–342. doi: 10.1016/S1937-6448(08)00632-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Suntharalingam M, Wente SR. Peering through the pore: nuclear pore complex structure, assembly, and function. Dev Cell. 2003;4:775–589. doi: 10.1016/s1534-5807(03)00162-x. [DOI] [PubMed] [Google Scholar]
- 23.Denning DP, Patel SS, Uversky V, Fink AL, Rexach M. Disorder in the nuclear pore complex: the FG repeat regions of nucleoporins are natively unfolded. Proc Natl Acad Sci USA. 2003;100:2450–5. doi: 10.1073/pnas.0437902100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Rout MP, Aitchison JD, Suprapto A, Hjertaas K, Zhao Y, Chait BT. The yeast nuclear pore complex: composition, architecture, and transport mechanism. J Cell Biol. 2000;148:635–51. doi: 10.1083/jcb.148.4.635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Strawn LA, Shen T, Shulga N, Goldfarb DS, Wente SR. Minimal nuclear pore complexes define FG repeat domains essential for transport. Nat Cell Biol. 2004;6:197–206. doi: 10.1038/ncb1097. [DOI] [PubMed] [Google Scholar]
- 26.Tran EJ, Wente SR. Dynamic nuclear pore complexes: life on the edge. Cell. 2006;125:1041–53. doi: 10.1016/j.cell.2006.05.027. [DOI] [PubMed] [Google Scholar]
- 27.Keminer O, Peters R. Permeability of single nuclear pores. Biophys J. 1999;77:217–28. doi: 10.1016/S0006-3495(99)76883-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chook YM, Süel KE. Nuclear import by karyopherin-βs: recognition and inhibition. Biochem Biophys Acta - Mol Cell Res. 2011;1813:1593–606. doi: 10.1016/j.bbamcr.2010.10.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Güttler T, Görlich D. Ran-dependent nuclear export mediators: a structural perspective. EMBO J. 2011;30:3457–74. doi: 10.1038/emboj.2011.287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jamali T, Jamali Y, Mehrbod M, Mofrad MRK. Nuclear pore complex: biochemistry and biophysics of nucleocytoplasmic transport in health and disease. Int Rev Cell Mol Biol. 2011;287:233–86. doi: 10.1016/B978-0-12-386043-9.00006-2. [DOI] [PubMed] [Google Scholar]
- 31.Wente SR, Rout MP. The nuclear pore complex and nuclear transport. Cold Spring Harb Perspect Biol. 2010;2:a000562. doi: 10.1101/cshperspect.a000562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chook YM, Blobel G. Karyopherins and nuclear import. Curr Opin Struct Biol. 2001;11:703–15. doi: 10.1016/s0959-440x(01)00264-0. [DOI] [PubMed] [Google Scholar]
- 33.Bischoff FR, Görlich D. RanBP1 is crucial for the release of RanGTP from importin β-related nuclear transport factors. FEBS Lett. 1997;419:249–54. doi: 10.1016/s0014-5793(97)01467-1. [DOI] [PubMed] [Google Scholar]
- 34.Bischoff FR, Klebe C, Kretschmer J, Wittinghofer A, Ponstingl H. RanGAP1 induces GTPase activity of nuclear Ras-related Ran. Proc Natl Acad Sci U S A. 1994;91:2587–91. doi: 10.1073/pnas.91.7.2587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Kutay U, Bischoff FR, Kostka S, Kraft R, Görlich D. Export of importin a from the nucleus is mediated by a specific nuclear transport factor. Cell. 1997;90:1061–71. doi: 10.1016/s0092-8674(00)80372-4. [DOI] [PubMed] [Google Scholar]
- 36.Devos D, Dokudovskaya S, Williams R, Alber F, Eswar N, Chait BT, Rout MP, Sali A. Simple fold composition and modular architecture of the nuclear pore complex. Proc Natl Acad Sci USA. 2006;103 doi: 10.1073/pnas.0506345103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Denning DP, Rexach MF. Rapid evolution exposes the boundaries of domain structure and function in natively unfolded FG nucleoporins. Mol Cell Proteomics. 2007;6:272–82. doi: 10.1074/mcp.M600309-MCP200. [DOI] [PubMed] [Google Scholar]
- 38.Yamada J, Phillips JL, Patel S, Goldfien G, Calestagne-Morelli A, Huang H, Rexza R, Acheson J, Krishnan VV, Newsam S, Gopinathan A, Lau EY, Colvin ME, Uversky VN, Rexach MF. A bimodal distribution of two distinct categories of intrinsically-disordered structures with separate functions in FG nucleoporins. Mol Cell Proteomics. 2010;9:2205–24. doi: 10.1074/mcp.M000035-MCP201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Frey S, Görlich D. FG/FxFG as well as GLFG repeats form a selective permeability barrier with self-healing properties. EMBO J. 2009;28:2554–67. doi: 10.1038/emboj.2009.199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lim RYH, Fahrenkrog B, Koser J, Schwarz-Herion K, Deng J, Aebi U. Nanomechanical basis of selective gating by the nuclear pore complex. Science. 2007;318:640–3. doi: 10.1126/science.1145980. [DOI] [PubMed] [Google Scholar]
- 41.Lim RYH, Huang NP, Koser J, Deng J, Lau KHA, Schwarz-Herion K, Fahrenkrog B, Aebi U. Flexible phenylalanine-glycine nucleoporins as entropic barriers to nucleocytoplasmic transport. Proc Natl Acad Sci USA. 2006;103:9512–7. doi: 10.1073/pnas.0603521103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Frey S, Richter RP, Görlich D. FG-rich repeats of nuclear pore proteins form a three-dimensional meshwork with hydrogel-like properties. Science. 2006;314:815–7. doi: 10.1126/science.1132516. [DOI] [PubMed] [Google Scholar]
- 43.Frey S, Görlich D. A saturated FG-repeat hydrogel can reproduce the permeability properties of nuclear pore complexes. Cell. 2007;130:512–23. doi: 10.1016/j.cell.2007.06.024. [DOI] [PubMed] [Google Scholar]
- 44.Eisele NB, Labokha AA, Frey S, Görlich D, Richter RP. Cohesiveness tunes assembly and morphology of FG nucleoporin domain meshworks - implications for nuclear pore permeability. Biophys J. 2013;105:1860–70. doi: 10.1016/j.bpj.2013.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hülsmann BB, Labokha AA, Görlich D. The permeability of reconstituted nuclear pores provides direct evidence for the selective phase model. Cell. 2012;150:738–51. doi: 10.1016/j.cell.2012.07.019. [DOI] [PubMed] [Google Scholar]
- 46.Patel SS, Belmont BJ, Sante JM, Rexach MF. Natively unfolded nucleoporins gate protein diffusion across the nuclear pore complex. Cell. 2007;129:83–96. doi: 10.1016/j.cell.2007.01.044. [DOI] [PubMed] [Google Scholar]
- 47.Eibauer M, Pellanda M, Turgay Y, Dubrovsky A, Wild A, Medalia O. Structure and gating of the nuclear pore complex. Nat Comm. 2015;6:7532. doi: 10.1038/ncomms8532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Schmidt HB, Görlich D. Nup98 FG domains from diverse species spontaneously phase-separate into particles with nuclear pore-like permselectivity. eLife. 2015;4:e04251. doi: 10.7554/eLife.04251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Tetenbaum-Novatt J, Hough LE, Mironska R, McKinney SA, Rout MP. Nucleocytoplasmic transport: a role for nonspecific competition in karyopherin-nucleoporin interactions. Mol Cell Proteomics. 2012;11:31–46. doi: 10.1074/mcp.M111.013656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Peters R. Translocation through the nuclear pore: Kaps pave the way. Bioessays. 2009;31:466–77. doi: 10.1002/bies.200800159. [DOI] [PubMed] [Google Scholar]
- 51.Tokunaga M, Imamoto N, Sakata-Sogawa K. Highly inclined thin illumination enables clear single-molecule imaging in cells. Nat Methods. 2008;5:159–61. doi: 10.1038/nmeth1171. [DOI] [PubMed] [Google Scholar]
- 52.Lowe AR, Tang JH, Yassif J, Graf M, Huang WYC, Groves JT, Weis K, Liphard JT. Importin-β modulates the permeability of the nuclear pore complex in a Ran-dependent manner. eLife. 2015;4:e04052. doi: 10.7554/eLife.04052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Paradise A, Levin MK, Korza G, Carson JH. Significant proportions of nuclear transport proteins with reduced intracellular mobilities resolved by fluorescence correlation spectroscopy. J Mol Biol. 2007;365:50–65. doi: 10.1016/j.jmb.2006.09.08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Jovanovic-Talisman T, Tetenbaum-Novatt J, McKinney SA, Zilman A, Peters R, Rout MP, Chait BT. Artificial nanopores that mimic the transport selectivity of the nuclear pore complex. Nature. 2009;457:1023–7. doi: 10.1038/nature07600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kapinos LE, Schoch RL, Wagner RS, Schleicher KD, Lim RYM. Karyophein-centric control of nuclear pores based on molecular occupancy and kinetic analysis of multivalent binding with FG nucleoporins. Biophys J. 2014;106:1751–62. doi: 10.1016/j.bpj.2014.02.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Schleicher KD, Dettmer SL, Kapinos LE, Pagliara S, Keyser UF, Jeney S, Lim RYH. Selective transport control on molecular velcro made from intrinsically disordered proteins. Nat Nanotech. 2014;9:525–30. doi: 10.1038/nnano.2014.103. [DOI] [PubMed] [Google Scholar]
- 57.Wagner RS, Kapinos LE, Marshall NJ, Stewart M, Lim RYH. Promiscuous binding of Karyopherin β1 modulates FG nucleoporin barrier function and expediates NTF2 transport kinetics. Biophys J. 2015;108:918–27. doi: 10.1016/j.bpj.2014.12.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Yang W, Musser SM. Nuclear import time and transport efficiency depend on importin β concentration. J Cell Biol. 2006;174:951–61. doi: 10.1083/jcb.200605053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Kustanovich T, Rabin Y. Metastable network model of protein transport through nuclear pores. Biophys J. 2004;86:2008–16. doi: 10.1016/S0006-3495(04)74262-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Tagliazucchi M, Peleg O, Kröger M, Rabin Y, Szleifer I. Effect of charge, hydrophobicity, and sequence of nucleoporins on the translocation of model particles through the nuclear pore complex Proc. Natl Acad Sci USA. 2013;110:3363–8. doi: 10.1073/pnas.1212909110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Moussavi-Baygi R, Jamali Y, Karimi R, Mofrad MRK. Brownian dynamics simulation of nucleocytoplasmic transport: a couarse-grained model for the functional state of the nuclear pore complex. PLoS Comp Biol. 2011;7 doi: 10.1371/journal.pcbi.1002049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Moussavi-Baygi R, Jamali Y, Karimi R, Mofrad MRK. Biophysical coarse-grained modeling provides insights into transport through the nuclear pore complex. Biophys J. 2011;100:1410–9. doi: 10.1016/j.bpj.2011.01.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Zilman A. Effects of multiple occupancy and inter-particle interactions on selective transport through narrow channels: theory versus experiment. Biophys J. 2009;96:1235–48. doi: 10.1016/j.bpj.2008.09.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Zilman A, Di Talia S, Chait BT, Rout MP, Magnasco MO. Efficiency, selectivity, and robustness of nucleocytoplasmic transport. PLoS Comp Biol. 2007;3:1281–90. doi: 10.1371/journal.pcbi.0030125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Zilman A, Pearson J, Bel G. Effects of jamming on nonequilibrium transport times in nanochannels. Phys Rev Lett. 2009;103:128103. doi: 10.1103/PhysRevLett.103.128103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Atkinson CE, Mattheyses AL, Kampmann M, Simon SM. Conserved spatial organization of FG domains in the nuclear pore complex. Biophys J. 2013;104:37–50. doi: 10.1016/j.bpj.2012.11.3823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Osmanovic D, Fassati A, Ford IJ, Hoogenboom BW. Physical modelling of the nuclear pore complex. Soft Matter. 2013;9:10442–51. [Google Scholar]
- 68.Miao L, Schulten K. Transport-related structures and processes of the nuclear pore complex studied through molecular dynamics. Structure. 2009;17:449–59. doi: 10.1016/j.str.2008.12.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Mincer JS, Simon SM. Simulations of nuclear pore transport yield mechanistic insights and quantitative predictions. Proc Natl Acad Sci USA. 2011;108:E351–E8. doi: 10.1073/pnas.1104521108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Opferman M, Coalson R, Jasnow D, Zilman A. Morphological control of grafted polymer films via attraction to small nanoparticle inclusions. Phys Rev E. 2012;86:1–7. doi: 10.1103/PhysRevE.86.031806. [DOI] [PubMed] [Google Scholar]
- 71.Opferman MG, Coalson RD, Jasnow D, Zilman A. Morphology of polymer brushes infiltrated by attractive nanoinclusions of various sizes. Langmuir. 2013;29:8584–91. doi: 10.1021/la4013922. [DOI] [PubMed] [Google Scholar]
- 72.Grünwald D, Singer RH, Rout M. Nuclear export dynamics of RNA-protein complexes. Nature. 2011;475:333–41. doi: 10.1038/nature10318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Yang W, Gelles J, Musser SM. Imaging of single-molecule translocation through nuclear pore complexes. Proc Natl Acad Sci USA. 2004;101:12887–92. doi: 10.1073/pnas.0403675101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Yang W, Musser SM. Visualizing single molecules transiting through nuclear pore complexes with narrow-field epifluorescence microscopy. Methods. 2006;39:3316–328. doi: 10.1016/j.ymeth.2006.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Dange T, Grunwald D, Grunwald A, Peters R, Kubitscheck U. Autonomy and robustness of translocation through the nuclear pore complex: a single-molecule study. J Cell Biol. 2008;183:77–86. doi: 10.1083/jcb.200806173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Kubitscheck U, Grunwald D, Hoekstra A, Rohleder D, Kues T, Siebrasse JP, Peters R. Nuclear transport of single molecules: dwell times at the nuclear pore. J Cell Biol. 2005;168:233–43. doi: 10.1083/jcb.200411005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Cheezum MK, Walker WF, Guilford WH. Quantitative comparison of algorithms for tracking single fluorescent particles. Biophys J. 2001;81:2378–88. doi: 10.1016/S0006-3495(01)75884-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Thompson RE, Larson DR, Webb WW. Precise nanometer localization analysis for individual fluorescent probes. Biophys J. 2002;82:2775–83. doi: 10.1016/S0006-3495(02)75618-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Ma J, Yang W. Three-dimensional distribution of transient interactions in the nuclear pore complex obtained from single molecule snapshots. Proc Natl Acad Sci USA. 2010;107:7305–10. doi: 10.1073/pnas.0908269107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Grünwald D, Singer R. In vivo imaging of labelled endogenous β-actin mRNA during nucleocytoplasmic transport. Nature. 2010;467:604–7. doi: 10.1038/nature09438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Görlich D, Panté N, Kutay U, Aebi U, Bischoff FR. Identification of different roles for RanGDP and RanGTP in nuclear protein import. EMBO J. 1996;15:5584–94. [PMC free article] [PubMed] [Google Scholar]
- 82.Gilchrist D, Rexach M. Molecular basis for the rapid dissociation of nuclear localization signals from karyopherin α in the nucleoplasm. J Biol Chem. 2003;278:51937–49. doi: 10.1074/jbc.M307371200. [DOI] [PubMed] [Google Scholar]
- 83.Matsuura Y, Stewart M. Nup50/Npap60 function in nuclear import complex disassembly and importin recycling. EMBO J. 2005;24:3681–9. doi: 10.1038/sj.emboj.7600843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Solsbacher J, Maurer P, Vogel F, Schlenstedt G. Nup2p, a yeast nucleoporin, functions in bidirectional transport of importin alpha. Mol Cell Biol. 2000;20:8468–79. doi: 10.1128/mcb.20.22.8468-8479.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Matsuura Y, Lange A, Harreman MT, Corbett AH, Stewart M. Structural basis for Nup2p function in cargo release and karyopherin recycling in nuclear import. EMBO J. 2003;22:5358–69. doi: 10.1093/emboj/cdg538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Liu SM, Stewart M. Structural basis for the high-affinity binding of nucleoporin Nup1p to the Saccharomyces cerevisiae importin-β homologue, Kap95p. J Mol Biol. 2005;349 doi: 10.1016/j.jmb.2005.04.003. [DOI] [PubMed] [Google Scholar]
- 87.Sun C, Yang W, Tu LC, Musser SM. Single molecule measurements of importin α/cargo complex dissociation at the nuclear pore. Proc Natl Acad Sci USA. 2008;105:8613–8. doi: 10.1073/pnas.0710867105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Sun C, Fu G, Ciziene D, Stewart M, Musser SM. Choreography of importin α/CAS complex assembly and disassembly at the nuclear pore complex. Proc Natl Acad Sci USA. 2013;110:E1584–E93. doi: 10.1073/pnas.1220610110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Reverter D, Lima CD. Insights into E3 ligase activity revealed by a SUMO-RanGAP1-Ubc9-Nup358 complex. Nature. 2005;435:687–92. doi: 10.1038/nature03588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Matunis MJ, Wu J, Blobel G. SUMO-1 modification and its role in targeting the RanGTPase-activating protein, RanGAP1, to the nuclear pore complex. J Cell Biol. 1998;140:499–509. doi: 10.1083/jcb.140.3.499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Mahajan R, Delphin C, Guan T, Gerace L, Melchior F. A small ubiquitin-related polypeptide involved in targeting RanGAP1 to nuclear pore complex protein RanBP2. Cell. 1997;88:97–107. doi: 10.1016/s0092-8674(00)81862-0. [DOI] [PubMed] [Google Scholar]
- 92.Seewald MJ, Körner C, Wittinghofer A, Vetter IR. RanGAP mediates GTP hydrolysis without and arginine finger. Nature. 2002;415:662–6. doi: 10.1038/415662a. [DOI] [PubMed] [Google Scholar]
- 93.Matsuura Y, Stewart M. Structural basis for the assembly of a nuclear export complex. Nature. 2004;432:872–7. doi: 10.1038/nature03144. [DOI] [PubMed] [Google Scholar]
- 94.Wu J, Matunis MJ, Kraemer D, Blobel G, C E. Nup358, a cytoplasmically exposed nucleoporin with peptide repeats, Ran-GTP binding sites, zinc fingers, a cyclophilin A homologous domain, and a leucine-rich zipper. J Biol Chem. 1995;270:14209–13. doi: 10.1074/jbc.270.23.14209. [DOI] [PubMed] [Google Scholar]
- 95.Yokoyama N, Hayashi N, Seki T, Panté N, Ohba T, Nishii K, Kuma K, Hayashida T, Miyata T, Aebi U, Fukuil M, Nishimoto T. A giant nucleopore protein that binds Ran/TC4. Nature. 1995;376:184–8. doi: 10.1038/376184a0. [DOI] [PubMed] [Google Scholar]
- 96.Akey CW, Radermacher M. Architecture of the Xenopus nuclear pore complex revealed by three-dimensional cryo-electron microscopy. J Cell Biol. 1993;122:1–19. doi: 10.1083/jcb.122.1.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Goldberg MW, Allen TD. The nuclear pore complex and lamina: three-dimensional structures and interactions determined by field emission in-lens scanning electron microscopy. J Mol Biol. 1996;257:848–65. doi: 10.1006/jmbi.1996.0206. [DOI] [PubMed] [Google Scholar]
- 98.Jarnik M, Aebi U. Toward a more complete 3-D structure of the nuclear pore complex. J Struct Biol. 1991;107:291–308. doi: 10.1016/1047-8477(91)90054-z. [DOI] [PubMed] [Google Scholar]
- 99.Tu LC, Fu G, Zilman A, Musser SM. Large cargo transport by nuclear pores: implications for the spatial organization of FG-nucleoporins. EMBO J. 2013;32:3220–30. doi: 10.1038/emboj.2013.239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Dingwall C, Sharnick SV, Laskey RA. A polypeptide domain that specifies migration of nucleoplasmin into the nucleus. Cell. 1982;30:449–58. doi: 10.1016/0092-8674(82)90242-2. [DOI] [PubMed] [Google Scholar]
- 101.Ribbeck K, Görlich D. The permeability barrier of nuclear pore complexes appears to operate via hydrophobic exclusion. EMBO J. 2002;21:2664–71. doi: 10.1093/emboj/21.11.2664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Milles S, Mercandante D, Aramburu IV, Jensen MR, Banterle N, Koehler C, Tyagi S, Clarke J, Shammas SL, Blackledge M, Gräter F, Lemke EA. Plasticity of an ultrafast interaction between nucleoporins and nuclear transport receptors. Cell. 2015;163:734–45. doi: 10.1016/j.cell.2015.09.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Lowe AR, Siegel JJ, Kalab P, Siu M, Weis K, Liphardt JT. Selectivity mechanism of the nuclear pore complex characterized by single cargo tracking. Nature. 2010;467:600–3. doi: 10.1038/nature09285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Macara IG. Transport into and out of the nucleus. Microbiol Mol Biol Rev. 2001;65:570–94. doi: 10.1128/MMBR.65.4.570-594.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Rexach M, Blobel G. Protein import into nuclei: association and dissociation reactions involving transport substrate, transport factors, and nucleoporins. Cell. 1995;83:683–92. doi: 10.1016/0092-8674(95)90181-7. [DOI] [PubMed] [Google Scholar]
- 106.Aitchison JD, Blobel G, Rout MP. Kap104p: a karyopherin involved in the nuclear transport of messenger RNA binding proteins. Science. 1996;274:624–7. doi: 10.1126/science.274.5287.624. [DOI] [PubMed] [Google Scholar]
- 107.Rout MP, Blobel G, Aitchison JD. A distinct nuclear import pathway used by ribosomal proteins. Cell. 1997;89:715–25. doi: 10.1016/s0092-8674(00)80254-8. [DOI] [PubMed] [Google Scholar]
- 108.Marelli M, Aitchison JD, Wozniak RW. Specific binding of the karyopherin Kap121p to a subunit of the nuclear pore complex containing Nup53p, Nup59p, and Nup170p. J Cell Biol. 1998;143:1813–30. doi: 10.1083/jcb.143.7.1813. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Floer M, Blobel G. Putative reaction intermediates in Crm1-mediated nuclear protein export. J Biol Chem. 1999;274:16279–86. doi: 10.1074/jbc.274.23.16279. [DOI] [PubMed] [Google Scholar]
- 110.Ma J, Goryaynov A, Sarma A, Yang W. Self-regulated viscous channel in the nuclear pore complex. Proc Natl Acad Sci USA. 2012;109:7326–31. doi: 10.1073/pnas.1201724109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Fiserova J, Richards SA, Wente SR, Goldberg MW. Facilited transport and diffusion take distinct spatial routes through the nuclear pore complex. J Cell Sci. 2010;123:2773–80. doi: 10.1242/jcs.070730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Qu X, Lykke-Andersen S, Nasser T, Saguez C, Bertrand E, Jensen TH, Moore C. Assembly of an export-competent mRNP is needed for efficient release of the 3’-end processing complex after polyadenylation. Mol Cell Biol. 2009;29:5327–38. doi: 10.1128/MCB.00468-09. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.McCloskey A, Taniguchi I, Shinmyozu K, Ohno M. hnRNP C tetramer measures RNA length to classify RNA polymerase II transcripts for export. Science. 2012;335:1643–6. doi: 10.1126/science.1218469. [DOI] [PubMed] [Google Scholar]
- 114.Ohno M. Size matters in RNA export. RNA Biol. 2012;9:1413–7. doi: 10.4161/rna.22569. [DOI] [PubMed] [Google Scholar]
- 115.Katahira J. mRNA export and the TREX complex. Biochim Biophys Acta. 2012;1819:507–13. doi: 10.1016/j.bbagrm.2011.12.001. [DOI] [PubMed] [Google Scholar]
- 116.Umlauf D, Bonnet J, Waharte F, Fournier M, Stierle M, Fischer B, Brino L, Devys D, Tora L. The human TREX-2 complex is stably associated with the nuclear pore basket. J Cell Sci. 2013;126:2656–67. doi: 10.1242/jcs.118000. [DOI] [PubMed] [Google Scholar]
- 117.Mor A, Suliman S, Ben-Yishay R, Yunger S, Brody Y, Shav-Tal Y. Dynamics of single mRNP nucleocytoplasmic transport and export through the nuclear pore in living cells. Nat Cell Biol. 2010;12:543–52. doi: 10.1038/ncb2056. [DOI] [PubMed] [Google Scholar]
- 118.Kiseleva E, Goldberg MW, Allen TD, Akey CW. Active nuclear pore complexes in Chironomus: visualization of transporter configurations related to mRNP export. J Cell Sci. 1998;111:223–36. doi: 10.1242/jcs.111.2.223. [DOI] [PubMed] [Google Scholar]
- 119.Siebrasse JP, Kaminski T, Kubitscheck U. Nuclear export of single native mRNA molecules observed by light sheet fluorescence microscopy. Proc Natl Acad Sci USA. 2012;109:9426–31. doi: 10.1073/pnas.1201781109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Ma J, Liu Z, Michelotti N, Pitchiaya S, Veerapaneni R, Androsavich JR, Walter NG, Yang W. High-resolution three-dimensional mapping of mRNA export through the nuclear pore. Nat Comm. 2013;4:2414. doi: 10.1038/ncomms3414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Saroumfim MA, Bensidoun P, Raymond P, Rahman S, Krause MR, Oeffinger M, Zenklusen D. The nuclear basket mediates perinuclear mRNA scanning in budding yeast. J Cell Biol. 2015;211:1131–40. doi: 10.1083/jcb.201503070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Smith CS, Lari A, Derrer CP, Ouwehand A, Rossouw A, Huisman M, Dange T, Hopman M, Joseph A, Zenklusen D, Weis K, Grunwald D, Montpetit B. In vivo single particle imaging of nuclear mRNA export in budding yeast. J Cell Biol. 2015;211:1121–30. doi: 10.1083/jcb.201503135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Smith CS, Preibisch S, Joseph A, Abrahamsson S, Rieger B, Myers E, Singer RH, Grunwald D. Nuclear accessibility of beta-actin mRNA is measured by 3D single-molecule real-time tracking. J Cell Biol. 2015;209:609–19. doi: 10.1083/jcb.201411032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.Krull S, Dorries J, Boysen B, Reidenbach S, Magnius L, Norder H, Thyberg J, Cordes VC. Protein Tpr is required for establishing nuclear pore-associated zones of heterochromatin exclusion. EMBO J. 2010;29:1659–73. doi: 10.1038/emboj.2010.54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Fiserova J, Spink M, Richards SA, Saunter C, Goldberg MW. Entry into the nuclear pore complex is controlled by a cytoplasmic exclusion zone containing dynamic GLFG-repeat nucleoporin domains. J Cell Sci. 2014;127:124–36. doi: 10.1242/jcs.133272. [DOI] [PubMed] [Google Scholar]
- 126.Park HY, Trcek T, Wells AL, Chao JA, Singer RH. An unbiased analysis method to quantify mRNA localization reveals its correlation with cell motility. Cell Rep. 2012;1:179–84. doi: 10.1016/j.celrep.2011.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Hocine S, Raymond P, Zenklusen D, Chao JA, Singer RH. Single-molecule analysis of gene expression using two-color RNA labeling in live yeast. Nat Methods. 2013;10:119–21. doi: 10.1038/nmeth.2305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Chao JA, Patskovsky Y, Almo SC, Singer RH. Structural basis for the coevolution of a viral RNA-protein complex. Nat Struct Mol Biol. 2008;15:103–5. doi: 10.1038/nsmb1327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Daigle N, Ellenberg J. LambdaN-GFP: an RNA reporter system for live-cell imaging. Nat Methods. 2007;4:633–6. doi: 10.1038/nmeth1065. [DOI] [PubMed] [Google Scholar]
- 130.Houman F, Diaz-Torres MR, Wright A. Transcriptional antitermination in the bgl operon of E. Coli is modulated by a specific RNA binding protein. Cell. 1990;62:1153–63. doi: 10.1016/0092-8674(90)90392-r. [DOI] [PubMed] [Google Scholar]
- 131.Chen J, Nikolaitchik O, Singh J, Wright A, Bencsics CE, Coffin JM, Ni N, Lockett S, Pathak VK, Hu WS. High efficiency of HIV-1 genomic RNA packaging and heterozygote formation revealed by single virion analysis. Proc Natl Acad Sci USA. 2009;106:13535–40. doi: 10.1073/pnas.0906822106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Batisse J, Batisse C, Budd A, Bottcher B, Hurt E. Purification of nuclear poly(A)-binding protein Nab2 reveals association with the yeast transcriptome and a messenger ribonucleoprotein core structure. J Biol Chem. 2009;284:34911–7. doi: 10.1074/jbc.M109.062034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Lonnroth A, Alexciev K, Mehlin H, Wurtz T, Skoglund U, Daneholt B. Demonstration of a 7-nm RNP fiber as the basic structural element in a premessenger RNP particle. Exp Cell Res. 1992;199:292–6. doi: 10.1016/0014-4827(92)90437-d. [DOI] [PubMed] [Google Scholar]
- 134.Singer RH, Penman S. Messenger RNA in HeLa cells: kinetics of formation and decay. J Mol Biol. 1973;78:321–34. doi: 10.1016/0022-2836(73)90119-8. [DOI] [PubMed] [Google Scholar]
- 135.Azimi M, Bulat E, Weis K, Mofrad MR. An agent-based model for mRNA export through the nuclear pore complex. Mol Biol Cell. 2014;25:3643–53. doi: 10.1091/mbc.E14-06-1065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Garcia JF, Parker R. MS2 coat proteins bound to yeast mRNAs block 5’ to 3’ degradation and trap mRNA decay products: implications for the localization of mRNAs by MS2-MCP system. RNA. 2015;21:1393–5. doi: 10.1261/rna.051797.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Siebrasse JP, Vieth R, Dobay A, Leonhardt H, Daneholt B, Kubitscheck U. Discontinuous movement of mRNP particles in nucleoplasmic regions devoid of chromatin. Proc Natl Acad Sci USA. 2008;105:20291–6. doi: 10.1073/pnas.0810692105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Tyagi S. Imaging intracellular RNA distribution and dynamics in living cells. Nat Meth. 2009;6:331–8. doi: 10.1038/nmeth.1321. [DOI] [PubMed] [Google Scholar]
- 139.Kummer S, Knoll A, Socher E, Bethge L, Herrmann A, Seitz O. Fluorescence imaging of influenza H1N1 mRNA in living infected cells using single-chromophore FIT-PNA. Angew Chem Int Ed. 2011;50:1931–4. doi: 10.1002/anie.201005902. [DOI] [PubMed] [Google Scholar]
- 140.Socher E, Knoll A, Seitz O. Dual fluorophore PNA FIT-probes – extremely responsive and bright hybridization probes for the sensitive detection of DNA and RNA. Org Biomol Chem. 2012;10:7363–71. doi: 10.1039/c2ob25925g. [DOI] [PubMed] [Google Scholar]
- 141.Rinne JS, Kaminski TP, Kubitscheck U, Heckel A. Light-inducible molecular beacons for spatio-temporally highly defined activation. Chem Comm. 2013;49:5375–7. doi: 10.1039/c3cc42420k. [DOI] [PubMed] [Google Scholar]
- 142.Dolgosheina EV, Jeng SC, Panchapakesan SS, Cojocaru R, Chen PS, Wilson PD, Hawkins N, Wiggins PA, Unrau PJ. RNA mango aptamer-fluorophore: a bright, high-affinity complex for RNA labeling and tracking. ACS Chem Biol. 2014;9:2412–20. doi: 10.1021/cb500499x. [DOI] [PubMed] [Google Scholar]
- 143.Strack RL, Disney MD, Jaffrey SR. A superfolding Spinach2 reveals the dynamic nature of trinucleotide repeat-containing RNA. Nat Meth. 2013;10:1219–24. doi: 10.1038/nmeth.2701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Filonov GS, Moon JD, Svensen N, Jaffrey SR. Broccoli: rapid selection of an RNA mimic of green fluorescent protein by fluorescence-based selection and directed evolution. J Am Chem Soc. 2014;136:16299–308. doi: 10.1021/ja508478x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Ma H, Naseri A, Reyes-Gutierrez P, Wolfe SA, Zhang S, Pederson T. Multicolor CRISPR labeling of chromosomal loci in human cells. Proc Natl Acad Sci USA. 2015;112:3002–7. doi: 10.1073/pnas.1420024112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Deng W, Shi X, Tjian R, Lionnet T, Singer RH. CASFISH: CRISPR/Cas9-mediated in situ labeling of genomic loci in fixed cells. Proc Natl Acad Sci USA. 2015 doi: 10.1073/pnas.1515692112. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Grimm JB, English BP, Chen J, Slaughter JP, Zhang Z, Revyakin A, Patel R, Macklin JJ, Normanno D, Singer RH, Lionnet T, Lavis LD. A general method to improve fluorophores for live-cell and single-molecule microscopy. Nat Meth. 2015;12:244–50. doi: 10.1038/nmeth.3256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 148.Huang B, Babcock H, Zhuang X. Breaking the diffraction barrier: super-resolution imaging in cells. Cell. 2010;143:1047–58. doi: 10.1016/j.cell.2010.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Liu Z, Lavis LD, Betzig E. Imaging live-cell dynamics and structure at the single-molecule level. Mol Cell. 2015;58:644–59. doi: 10.1016/j.molcel.2015.02.033. [DOI] [PubMed] [Google Scholar]
- 150.Heilemann M, van de Linde S, Schüttpelz M, Kasper R, Seefeldt B, Mukherjee A, Tinnefeld P, Sauer M. Subdiffraction-resolution fluorescence imaging with conventional fluorescent probes. Angew Chem Int Ed. 2008;47:6172–6. doi: 10.1002/anie.200802376. [DOI] [PubMed] [Google Scholar]
- 151.Löschberger A, van de Linde S, Dabauvalle MC, Rieger B, Heilemann M, Krohne G, Sauer M. Super-resolution imaging visualizes the eightfold symmetry of gp210 proteins around the nuclear pore complex and resolves the central channel with nanometer resolution. J Cell Sci. 2012;125:570–5. doi: 10.1242/jcs.098822. [DOI] [PubMed] [Google Scholar]
- 152.Finlay DR, Newmeyer DD, Price TM, Forbes DJ. Inhibition of in vitro nuclear transport by a lectin that binds to nuclear pores. J Cell Biol. 1987;104:189–200. doi: 10.1083/jcb.104.2.189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Akey CW, Goldfarb DS. Protein import through the nuclear pore complex is a multistep process. J Cell Biol. 1989;1989:971–82. doi: 10.1083/jcb.109.3.971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Löschberger A, Franke C, Krohne G, van de Linde S, Sauer M. Correlative super-resolution fluorescence and electron microscopy of the nuclear pore complex with molecular resolution. J Cell Sci. 2014;127:4351–5. doi: 10.1242/jcs.156620. [DOI] [PubMed] [Google Scholar]
- 155.Hinshaw JE, Milligan RA. Nuclear pore complexes exceeding eightfold rotational symmetry. J Struct Biol. 2003;141:259–68. doi: 10.1016/s1047-8477(02)00626-3. [DOI] [PubMed] [Google Scholar]
- 156.Ori A, Banterle N, Iskar M, Andrés-Pons A, Escher C, Bui HK, Sparks L, Solis-Mezarino V, Rinner O, Bork P, Lemke EA, Beck M. Cell type-specific nuclear pores: a case in point for context-dependent stoichiometry of molecular machines. Mol Syst Biol. 2013;9:648. doi: 10.1038/msb.2013.4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Betzig E, Patterson GH, Sougrat R, Lindwasser OW, Olenych S, Bonifacino JS, Davidson MW, Lippincott-Schwartz J, Hess HF. Imaging intracellular fluorescent proteins at nanometer resolution. Science. 2006;313:1642–5. doi: 10.1126/science.1127344. [DOI] [PubMed] [Google Scholar]
- 158.Ulbrich MH, Isacoff EY. Subunit counting in membrane-bound proteins. Nat Meth. 2007;4:319–21. doi: 10.1038/NMETH1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 159.Annibale P, Vanni S, Scarselli M, Rothlisberger U, Radenovic A. Quantitative photoactivated localization microscopy: unraveling the effects of photoblinking. PLoS One. 2011;6:e22678. doi: 10.1371/journal.pone.0022678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.Durisic N, Laparra-Cuervo L, Sandoval-Álvarez Á, Borbely JS, Lakadamyali M. Single-molecule evaluation of fluorescent protein photoactivation efficiency using an in vivo template. Nat Meth. 2014;11:156–62. doi: 10.1038/nmeth.2784. [DOI] [PubMed] [Google Scholar]
- 161.Mi L, Goryaynov A, Lindquist A, Rexach MF, Yang W. Quantifying nucleoporin stoichiometry inside single nuclear pore complexes in vivo. Sci Rep. 2015;5:9372. doi: 10.1038/srep09372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 162.Alber F, Dokudovskaya S, Veenhoff LM, Zhang W, Kipper J, Devos D, Suprapto A, Karni-Schmidt O, Williams R, Chait BT, Rout MP, Sali A. Determining the architectures of macromolecular assemblies. Nature. 2007;450:683–94. doi: 10.1038/nature06404. [DOI] [PubMed] [Google Scholar]
- 163.Alber F, Dokudovskaya S, Veenhoff LM, Zhang W, Kipper J, Devos D, Suprapto A, Karni-Schmidt O, Williams R, Chait BT, Sali A, Rout MP. The molecular architecture of the nuclear pore complex. Nature. 2007;450:695–701. doi: 10.1038/nature06405. [DOI] [PubMed] [Google Scholar]
- 164.Kelley K, Knockenhauer KE, Kabachinski G, Schwartz TU. Atomic structure of the Y complex of the nuclear pore. Nat Struct Mol Biol. 2015;22:425–31. doi: 10.1038/nsmb.2998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Szymborska A, de Marco A, Daigle N, Cordes VC, Briggs JAG, Ellenberg J. Nuclear pore scaffold structure analyzed by super-resolution microscopy and particle averaging. Science. 2013;341 doi: 10.1126/science.1240672. [DOI] [PubMed] [Google Scholar]
- 166.Bretschneider S, Eggeling C, Hell SW. Breaking the diffraction barrier in fluorescence microscopy by optical shelving. Phys Rev Lett. 2007;98:218103. doi: 10.1103/PhysRevLett.98.218103. [DOI] [PubMed] [Google Scholar]
- 167.Kampmann M, Atkinson CE, Mattheyses AL, Simon SM. Mapping the orientation of nuclear pore proteins in living cells with polarized fluorescence microscopy. Nat Struct Mol Biol. 2011;18:643–9. doi: 10.1038/nsmb.2056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Stuwe T, Correia AR, Lin DH, Paduch M, Lu VT, Kossiakoff AA, Hoelz A. Architecture of the nuclear pore complex coat. Science. 2015;347:1148–52. doi: 10.1126/science.aaa4136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Bui KH, von Appen A, DiGuillo AL, Ori A, Sparks L, Mackmull MT, Bock T, Hagen W, Andrés-Pons A, Glavy JS, Beck M. Integrated structural analysis of the human nuclear pore complex scaffold. Cell. 2013;155:1233–43. doi: 10.1016/j.cell.2013.10.055. [DOI] [PubMed] [Google Scholar]
- 170.Abraham AV, Ram S, Chao J, Ward SE, Ober RJ. Quantitative study of single molecule location estimation techniques. Opt Express. 2009;17:23352–73. doi: 10.1364/OE.17.023352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Mortensen KI, Churchman LS, Spudich JA, Flyvbjerg H. Optimized localization analysis for single-molecule tracking and super-resolution microscopy. Nat Meth. 2010;7:377–81. doi: 10.1038/nmeth.1447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Ober RJ, Ram S, Ward ES. Localization accuracy in single-molecule microscopy. Biophys J. 2004;86:1185–200. doi: 10.1016/S0006-3495(04)74193-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Smith CS, Joseph A, Rieger B, Lidke KA. Fast, single-molecule localization that achieves theoretically minimum uncertainty. Nat Meth. 2010;7:373–5. doi: 10.1038/nmeth.1449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174.Quan T, Zheng S, Huang ZL. Localization capability and limitation of electron-multiplying charge-coupled, scientific complementary metal-oxide semiconductor, and charge-coupled devices for superresolution imaging. J Biomed Opt. 2010;15 doi: 10.1117/1.3505017. 066005. [DOI] [PubMed] [Google Scholar]
- 175.Robbins MS, Hadwen BJ. The noise performance of electron multiplying charge-coupled devices. IEEE Trans Electr Dev. 2003;50:1227–32. [Google Scholar]
- 176.Deschout H, Neyts K, Braeckmans K. The influence of movement on the localization precision of sub-resolution particles in fluorescence microscopy. J Biophotonics. 2012;5:97–109. doi: 10.1002/jbio.201100078. [DOI] [PubMed] [Google Scholar]
- 177.Churchman LS, Ökten Z, Rock RS, Dawson JF, Spudich JA. Single molecule high-resolution colocalization of Cy3 and Cy5 attached to macromolecules measures intramolecular distances through time. Proc Natl Acad Sci USA. 2005;102:1419–23. doi: 10.1073/pnas.0409487102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 178.Chao J, Ram S, Lee T, Ward SE, Ober RJ. Investigation of the numerics of point spread function integration in single molecule localization. Opt Express. 2015;23:16866–83. doi: 10.1364/OE.23.016866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 179.Stallinga S, Rieger B. Position and orientation estimation of fixed dipole emitters using an effective Hermite point spread function model. Opt Express. 2012;20:5896–921. doi: 10.1364/OE.20.005896. [DOI] [PubMed] [Google Scholar]
- 180.Stallinga S. Effect of rotational diffusion in an orientational potential well on the point spread function of electric dipole emitters. J Opt Soc Amer A. 2015;32:213–23. doi: 10.1364/JOSAA.32.000213. [DOI] [PubMed] [Google Scholar]
- 181.Enderlein J, Toprak E, Selvin PR. Polarizationa effect on position accuracy of fluorophore localization. Opt Express. 2006;14:8111–20. doi: 10.1364/oe.14.008111. [DOI] [PubMed] [Google Scholar]
- 182.Lew MD, Backlund MP, Moerner WE. Rotational mobility of single molecules affects localization accuracy in super-resolution fluorescence microscopy. Nano Lett. 2013;13:3967–72. doi: 10.1021/nl304359p. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183.Stallinga S, Rieger B. Accuracy of the Gaussian point spread function model in 2D localization microscopy. Opt Express. 2010;18:24461–76. doi: 10.1364/OE.18.024461. [DOI] [PubMed] [Google Scholar]
- 184.Engelhardt J, Keller J, Hoyer P, Reuss M, Staudt T, Hell SW. Molecular orientation affects localization accuracy in superresolution far-field fluorescence microscopy. Nano Lett. 2011;11:209–13. doi: 10.1021/nl103472b. [DOI] [PubMed] [Google Scholar]
- 185.Lew MD, Moerner WE. Azimuthal polarization filtering for accurate, precise, and robust single-molecule localization microscopy. Nano Lett. 2014;14:6407–13. doi: 10.1021/nl502914k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186.Goryaynov A, Yang W. Role of molecular charge in nucleocytoplasmic transport. PLoS One. 2014;9:e88792. doi: 10.1371/journal.pone.0088792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 187.Ram S, Prabhat P, Chao J, Ward SW, Ober RJ. High accuracy 3D quantum dot tracking with multifocal plane microscopy for the study of fast intracellular dynamics in live cells. Biophys J. 2008;95:6025–43. doi: 10.1529/biophysj.108.140392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 188.Pavani SRP, Thompson MA, Biteen JS, Lord SJ, Liu N, Tweig RJ, Piestun R, Moerner WE. Three-dimensional, single-molecule fluorescence imaging beyond the diffraction limit by using a double-helix point spread function. Proc Natl Acad Sci USA. 2009;106:2995–9. doi: 10.1073/pnas.0900245106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 189.Lien CH, Lin CY, Cahen SJ, Chien FC. Dynamic particle tracking via temporal focusing multiphoton microscopy with astigmatism imaging. Opt Express. 2014;22:27290–9. doi: 10.1364/OE.22.027290. [DOI] [PubMed] [Google Scholar]
- 190.Lew MD, Lee SF, Badieirostami M, Moerner WE. Corckscrew point spread function for far-field three-dimensional nanoscale localization of pointlike objects. Opt Lett. 2011;36:202–4. doi: 10.1364/OL.36.000202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 191.Abrahamsson S, Chen J, Hajj B, Stallinga S, Katsov AY, Wisniewski J, Mizuguchi G, Soule P, Mueller F, Dugast Darzacq C, Darzacq X, Wu C, Bargmann CI, Agard DA, Dahan M, Gustafsson MG. Fast multicolor 3D imaging using aberration-corrected multifocus microscopy. Nat l Meth. 2013;10:60–3. doi: 10.1038/nmeth.2277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 192.Nieuwenhuizen RP, Lidke KA, Bates M, Puig DL, Grunwald D, Stallinga S, Rieger B. Measuring image resolution in optical nanoscopy. Nat Meth. 2013;10:557–62. doi: 10.1038/nmeth.2448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 193.Smith CS, Stallinga S, Lidke KA, Rieger B, Grünwald D. Probability-based particle detection that enables threshold-free and robust in vivo single-molecule tracking. Mol Biol Cell. 2015;26:4057–62. doi: 10.1091/mbc.E15-06-0448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 194.Pleiner T, Bates M, Trakhanov S, Lee CT, Schliep JE, Chug H, Böhning M, Stark H, Urlaub H, Görlich D. Nanobodies: site-specific labeling for super-resolution imaging, rapid epitope-mapping, and native protein complex isolation. eLife. 2016;4:e11349. doi: 10.7554/eLife.11349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 195.Dworetzky SI, Feldherr CM. Translocation of RNA-coated gold particles through the nuclear pores of oocytes. J Cell Biol. 1988;106:575–84. doi: 10.1083/jcb.106.3.575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 196.Kapon R, Topchik A, Mukamel D, Reich Z. A possible mechanism for self-coordination of bidirectional traffic across nuclear pores. Phys Biol. 2008;5:036001. doi: 10.1088/1478-3975/5/3/036001. [DOI] [PubMed] [Google Scholar]
- 197.Natalizio BJ, Wente SR. Postage for the messenger: designating routes for nuclear mRNA export. Trends Cell Biol. 2013;23:365–73. doi: 10.1016/j.tcb.2013.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 198.Elton D, Amorim MJ, Medcalf L, Digard P. ‘Genome gating’; polarized intranuclear trafficking of influenza virus RNPs. Biol Lett. 2005;1:113–7. doi: 10.1098/rsbl.2004.0253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 199.Park HY, Lim H, Yoon YJ, Follenzi A, Nwokafor C, Lopez-Jones M, Meng X, Singer RH. Visualization of dynamics of single endogenous mRNA labeled in live mouse. Science. 2014;343:422–4. doi: 10.1126/science.1239200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 200.Roth DM, Moseley GW, Pouton CW, Jans DA. Mechanism of microtubule-facilitated “fast track” nuclear import. J Biol Chem. 2011;286:14335–51. doi: 10.1074/jbc.M110.210302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 201.Chao J, Ward ES, Ober RJ. Fisher information matrix for branching processes with application to electron-multiplying charge-coupled devices. Multidim Syst Sign P. 2012;23:349–79. doi: 10.1007/s11045-011-0150-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202.Tahmasbi A, Ram S, Chao J, Abraham AV, Tang FW, Ward ES, Ober RJ. Designing the focal plane spacing for multifocal plane microscopy. Opt Express. 2014;22:16706–21. doi: 10.1364/OE.22.016706. [DOI] [PMC free article] [PubMed] [Google Scholar]