Нейросеть | это... Что такое Нейросеть? (original) (raw)
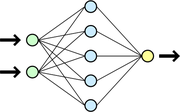
Схема простой нейросети. Зелёным обозначены входные элементы, жёлтым — выходной элемент
Иску́сственные нейро́нные се́ти (ИНС) — математические модели, а также их программные или аппаратные реализации, построенные по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма. Это понятие возникло при изучении процессов, протекающих в мозге при мышлении, и при попытке смоделировать эти процессы. Первой такой моделью мозга был перцептрон. Впоследствии эти модели стали использовать в практических целях, как правило в задачах прогнозирования.
ИНС представляют собой систему соединённых и взаимодействующих между собой простых процессоров (искусственных нейронов). Такие процессоры обычно довольно просты, особенно в сравнении с процессорами, используемыми в персональных компьютерах. Каждый процессор подобной сети имеет дело только с сигналами, которые он периодически получает, и сигналами, которые он периодически посылает другим процессорам. И тем не менее, будучи соединёнными в достаточно большую сеть с управляемым взаимодействием, такие локально простые процессоры вместе способны выполнять довольно сложные задачи.
С точки зрения машинного обучения, нейронная сеть представляет собой частный случай методов распознавания образов, дискриминантного анализа, методов кластеризации и т. п. С математической точки зрения обучение нейронных сетей, это многопараметрическая задача нелинейной оптимизации. С точки зрения кибернетики, нейронная сеть используется в задачах адаптивного управления и как алгоритмы для робототехники. С точки зрения развития вычислительной техники и программирования, нейронная сеть — способ решения проблемы эффективного параллелизма. А с точки зрения искусственного интеллекта, ИНС является основой философского течения коннективизма и основным направлением в структурном подходе по изучению возможности построения (моделирования) естественного интеллекта с помощью компьютерных алгоритмов.
Нейронные сети не программируются в привычном смысле этого слова, они обучаются. Возможность обучения — одно из главных преимуществ нейронных сетей перед традиционными алгоритмами. Технически обучение заключается в нахождении коэффициентов связей между нейронами. В процессе обучения нейронная сеть способна выявлять сложные зависимости между входными данными и выходными, а также выполнять обобщение. Это значит, что, в случае успешного обучения, сеть сможет вернуть верный результат на основании данных, которые отсутствовали в обучающей выборке.
Содержание
- 1 Хронология
- 2 Известные применения
- 3 Этапы решения задач
- 4 Классификация по типу входной информации
- 5 Классификация по характеру обучения
- 6 Классификация по характеру настройки синапсов
- 7 Классификация по времени передачи сигнала
- 8 Классификация по характеру связей
- 9 Известные типы сетей
- 10 Отличия от машин с архитектурой фон Неймана
- 11 Нейронные сети — универсальные аппроксиматоры
- 12 Примеры приложений
- 13 См. также
- 14 Примечания
- 15 Ссылки
- 16 Литература
Хронология
- 1943 год — Норберт Винер вместе с соратниками публикует работу о кибернетике. Основной идеей является представление сложных биологических процессов математическими моделями.
- 1943 год — Маккалок и Питтс формализуют понятие нейронной сети в фундаментальной статье о логическом исчислении идей и нервной активности[1].
- 1949 год — Хебб предлагает первый алгоритм обучения.
- В 1958 году Розенблаттом изобретен перцептрон. Перцептрон обретает популярность — его используют для распознавания образов, прогнозирования погоды и т. д. Казалось, что построение полноценного искусственного интеллекта уже не за горами.
- В 1960 году Уидроу (Widrow) совместно со своим студентом Хоффом на основе дельта-правила (формулы Уидроу) разработали Адалин, который сразу начал использоваться для задач предсказания и адаптивного управления. Адалин был построен на базе созданных ими же (Уидроу — Хоффом) принципально новых элементах — мемисторах[2]. Сейчас Адалин (адаптивный сумматор) является стандартным элементом многих систем обработки сигналов.[3]
- В 1961 году под руководством М. М. Бонгарда разработана программа «Кора»: «…задача Коры — поиск разделяющего правила после того, как найдены операторы, дающие достаточно четкие (коротко кодируемые) характеристики объекта или его частей». Программа Кора нашла применение, в частности, для распознавания нефтеносных пластов.
- В 1969 году Минский публикует формальное доказательство ограниченности перцептрона и показывает, что он неспособен решать некоторые задачи (Проблема "четности" и "один в блоке"), связанные с инвариантностью представлений. Интерес к нейронным сетям резко спадает.
- 1974 год — Пол Дж. Вербос[4] и А. И. Галушкин[5] одновременно изобретают алгоритм обратного распространения ошибки для обучения многослойных перцептронов. Изобретение не привлекло особого внимания.
- 1975 год — Фукушима представляет Когнитрон — самоорганизующуюся сеть, предназначенную для инвариантного распознавания образов, но это достигается только при помощи запоминания практически всех состояний образа.
- 1982 год — после длительного упадка, интерес к нейросетям вновь возрастает. Хопфилд показал, что нейронная сеть с обратными связями может представлять собой систему, минимизирующую энергию (так называемая сеть Хопфилда). Кохоненом представлены модели сети, обучающейся без учителя (Нейронная сеть Кохонена), решающей задачи кластеризации, визуализации данных (самоорганизующаяся карта Кохонена) и другие задачи предварительного анализа данных.
- 1986 год — Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом[6] и независимо и одновременно С. И. Барцевым и В. А. Охониным (Красноярская группа)[7] переоткрыт и существенно развит метод обратного распространения ошибки. Начался взрыв интереса к обучаемым нейронным сетям.
Известные применения
Распознавание образов и классификация
В качестве образов могут выступать различные по своей природе объекты: символы текста, изображения, образцы звуков и т. д. При обучении сети предлагаются различные образцы образов с указанием того, к какому классу они относятся. Образец, как правило, представляется как вектор значений признаков. При этом совокупность всех признаков должна однозначно определять класс, к которому относится образец. В случае, если признаков недостаточно, сеть может соотнести один и тот же образец с несколькими классами, что неверно [8]. По окончании обучения сети ей можно предъявлять неизвестные ранее образы и получать ответ о принадлежности к определённому классу.
Топология такой сети характеризуется тем, что количество нейронов в выходном слое, как правило, равно количеству определяемых классов. При этом устанавливается соответствие между выходом нейронной сети и классом, который он представляет. Когда сети предъявляется некий образ, на одном из её выходов должен появиться признак того, что образ принадлежит этому классу. В то же время на других выходах должен быть признак того, что образ данному классу не принадлежит[9]. Если на двух или более выходах есть признак принадлежности к классу, считается что сеть «не уверена» в своём ответе.
Принятие решений и управление
Эта задача близка к задаче классификации. Классификации подлежат ситуации, характеристики которых поступают на вход нейронной сети. На выходе сети при этом должен появится признак решения, которое она приняла. При этом в качестве входных сигналов используются различные критерии описания состояния управляемой системы[10].
Кластеризация
Под кластеризацией понимается разбиение множества входных сигналов на классы, при том, что ни количество, ни признаки классов заранее неизвестны. После обучения такая сеть способна определять, к какому классу относится входной сигнал. Сеть также может сигнализировать о том, что входной сигнал не относится ни к одному из выделенных классов — это является признаком новых, отсутствующих в обучающей выборке, данных. Таким образом, подобная сеть может выявлять новые, неизвестные ранее классы сигналов. Соответствие между классами, выделенными сетью, и классами, существующими в предметной области, устанавливается человеком. Кластеризацию осуществляют, например, нейронные сети Кохонена.
Прогнозирование и аппроксимация
Способности нейронной сети к прогнозированию напрямую следуют из ее способности к обобщению и выделению скрытых зависимостей между входными и выходными данными. После обучения сеть способна предсказать будущее значение некой последовательности на основе нескольких предыдущих значений и/или каких-то существующих в настоящий момент факторов. Следует отметить, что прогнозирование возможно только тогда, когда предыдущие изменения действительно в какой-то степени предопределяют будущие. Например, прогнозирование котировок акций на основе котировок за прошлую неделю может оказаться успешным (а может и не оказаться), тогда как прогнозирование результатов завтрашней лотереи на основе данных за последние 50 лет почти наверняка не даст никаких результатов.
Сжатие данных и Ассоциативная память
Способность нейросетей к выявлению взаимосвязей между различными параметрами дает возможность выразить данные большой размерности более компактно, если данные тесно взаимосвязаны друг с другом. Обратный процесс — восстановление исходного набора данных из части информации — называется (авто)ассоциативной памятью. Ассоциативная память позволяет также восстанавливать исходный сигнал/образ из зашумленных/поврежденных входных данных. Решение задачи гетероассоциативной памяти позволяет реализовать память, адресуемую по содержимому[10].
Этапы решения задач
- Сбор данных для обучения;
- Подготовка и нормализация данных;
- Выбор топологии сети;
- Экспериментальный подбор характеристик сети;
- Экспериментальный подбор параметров обучения;
- Собственно обучение;
- Проверка адекватности обучения;
- Корректировка параметров, окончательное обучение;
- Вербализация сети[11] с целью дальнейшего использования.
Следует рассмотреть подробнее некоторые из этих этапов.
Сбор данных для обучения
Выбор данных для обучения сети и их обработка является самым сложным этапом решения задачи. Набор данных для обучения должен удовлетворять нескольким критериям:
- Репрезентативность — данные должны иллюстрировать истинное положение вещей в предметной области;
- Непротиворечивость — противоречивые данные в обучающей выборке приведут к плохому качеству обучения сети;
Исходные данные преобразуются к виду, в котором их можно подать на входы сети. Каждая запись в файле данных называется обучающей парой или обучающим вектором. Обучающий вектор содержит по одному значению на каждый вход сети и, в зависимости от типа обучения (с учителем или без), по одному значению для каждого выхода сети. Обучение сети на «сыром» наборе, как правило, не даёт качественных результатов. Существует ряд способов улучшить «восприятие» сети.
- Нормировка выполняется, когда на различные входы подаются данные разной размерности. Например, на первый вход сети подается величины со значениями от нуля до единицы, а на второй — от ста до тысячи. При отсутствии нормировки значения на втором входе будут всегда оказывать существенно большее влияние на выход сети, чем значения на первом входе. При нормировке размерности всех входных и выходных данных сводятся воедино;
- Квантование выполняется над непрерывными величинами, для которых выделяется конечный набор дискретных значений. Например, квантование используют для задания частот звуковых сигналов при распознавании речи;
- Фильтрация выполняется для «зашумленных» данных.
Кроме того, большую роль играет само представление как входных, так и выходных данных. Предположим, сеть обучается распознаванию букв на изображениях и имеет один числовой выход — номер буквы в алфавите. В этом случае сеть получит ложное представление о том, что буквы с номерами 1 и 2 более похожи, чем буквы с номерами 1 и 3, что, в общем, неверно. Для того, чтобы избежать такой ситуации, используют топологию сети с большим числом выходов, когда каждый выход имеет свой смысл. Чем больше выходов в сети, тем большее расстояние между классами и тем сложнее их спутать.
Выбор топологии сети
Выбирать тип сети следует исходя из постановки задачи и имеющихся данных для обучения. Для обучения с учителем требуется наличие для каждого элемента выборки «экспертной» оценки. Иногда получение такой оценки для большого массива данных просто невозможно. В этих случаях естественным выбором является сеть, обучающаяся без учителя, например, самоорганизующаяся карта Кохонена или нейронная сеть Хопфилда. При решении других задач, таких как прогнозирование временных рядов, экспертная оценка уже содержится в исходных данных и может быть выделена при их обработке. В этом случае можно использовать многослойный перцептрон или сеть Ворда.
Экспериментальный подбор характеристик сети
После выбора общей структуры нужно экспериментально подобрать параметры сети. Для сетей, подобных перцептрону, это будет число слоев, число блоков в скрытых слоях (для сетей Ворда), наличие или отсутствие обходных соединений, передаточные функции нейронов. При выборе количества слоев и нейронов в них следует исходить из того, что способности сети к обобщению тем выше, чем больше суммарное число связей между нейронами. С другой стороны, число связей ограничено сверху количеством записей в обучающих данных.
Экспериментальный подбор параметров обучения
После выбора конкретной топологии, необходимо выбрать параметры обучения нейронной сети. Этот этап особенно важен для сетей, обучающихся с учителем. От правильного выбора параметров зависит не только то, насколько быстро ответы сети будут сходиться к правильным ответам. Например, выбор низкой скорости обучения увеличит время схождения, однако иногда позволяет избежать паралича сети. Увеличение момента обучения может привести как к увеличению, так и к уменьшению времени сходимости, в зависимости от формы поверхности ошибки. Исходя из такого противоречивого влияния параметров, можно сделать вывод, что их значения нужно выбирать экспериментально, руководствуясь при этом критерием завершения обучения (например, минимизация ошибки или ограничение по времени обучения).
Собственно обучение сети
В процессе обучения сеть в определенном порядке просматривает обучающую выборку. Порядок просмотра может быть последовательным, случайным и т. д. Некоторые сети, обучающиеся без учителя, например, сети Хопфилда просматривают выборку только один раз. Другие, например, сети Кохонена, а также сети, обучающиеся с учителем, просматривают выборку множество раз, при этом один полный проход по выборке называется эпохой обучения. При обучении с учителем набор исходных данных делят на две части — собственно обучающую выборку и тестовые данные; принцип разделения может быть произвольным. Обучающие данные подаются сети для обучения, а проверочные используются для расчета ошибки сети (проверочные данные никогда для обучения сети не применяются). Таким образом, если на проверочных данных ошибка уменьшается, то сеть действительно выполняет обобщение. Если ошибка на обучающих данных продолжает уменьшаться, а ошибка на тестовых данных увеличивается, значит, сеть перестала выполнять обобщение и просто «запоминает» обучающие данные. Это явление называется переобучением сети или оверфиттингом. В таких случаях обучение обычно прекращают. В процессе обучения могут проявиться другие проблемы, такие как паралич или попадание сети в локальный минимум поверхности ошибок. Невозможно заранее предсказать проявление той или иной проблемы, равно как и дать однозначные рекомендации к их разрешению.
Проверка адекватности обучения
Даже в случае успешного, на первый взгляд, обучения сеть не всегда обучается именно тому, чего от неё хотел создатель. Известен случай, когда сеть обучалась распознаванию изображений танков по фотографиям, однако позднее выяснилось, что все танки были сфотографированы на одном и том же фоне. В результате сеть «научилась» распознавать этот тип ландшафта, вместо того, чтобы «научиться» распознавать танки[12]. Таким образом, сеть «понимает» не то, что от неё требовалось, а то, что проще всего обобщить.
Классификация по типу входной информации
- Аналоговые нейронные сети (используют информацию в форме действительных чисел);
- Двоичные нейронные сети (оперируют с информацией, представленной в двоичном виде).
Классификация по характеру обучения
- Обучение с учителем — выходное пространство решений нейронной сети известно;
- Обучение без учителя — нейронная сеть формирует выходное пространство решений только на основе входных воздействий. Такие сети называют самоорганизующимися;
- Обучение с подкреплением — система назначения штрафов и поощрений от среды.
Классификация по характеру настройки синапсов
- Сети с фиксированными связями (весовые коэффициенты нейронной сети выбираются сразу, исходя из условий задачи, при этом:
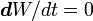 , где W — весовые коэффициенты сети);
, где W — весовые коэффициенты сети); - сети с динамическими связями (для них в процессе обучения происходит настройка синаптических связей, то есть
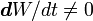 , где W — весовые коэффициенты сети).
, где W — весовые коэффициенты сети).
Классификация по времени передачи сигнала
В ряде нейронных сетей активирующая функция может зависеть не только от весовых коэффициентов связей w i j, но и от времени передачи импульса (сигнала) по каналам связи τ_i_ j. По этому в общем виде активирующая (передающая) функция связи c i j от элемента u i к элементу u j имеет вид: ![c_{ij}^* = f [ w_{ij}(t), u_i^*(t - \tau_{ij}) ]](https://dic.academic.ru/pictures/wiki/files/101/e6227b086a59fb96bb55904c79f237b5.png) . Тогда синхронной сетью называют такую сеть у которой время передачи τ_i_ j каждой связи равна либо нулю, либо фиксированной постоянной τ. Асинхронной называют такую сеть у которой время передачи τ_i_ j для каждой связи между элементами u i и u j свое, но тоже постоянное.
. Тогда синхронной сетью называют такую сеть у которой время передачи τ_i_ j каждой связи равна либо нулю, либо фиксированной постоянной τ. Асинхронной называют такую сеть у которой время передачи τ_i_ j для каждой связи между элементами u i и u j свое, но тоже постоянное.
Классификация по характеру связей
Сети прямого распространения (Feedforward)
Все связи направлены строго от входных нейронов к выходным. Примерами таких сетей являются перцептрон Розенблатта, многослойный перцептрон, сети Ворда.
Рекуррентные нейронные сети
Сигнал с выходных нейронов или нейронов скрытого слоя частично передается обратно на входы нейронов входного слоя (обратная связь). Рекуррентная сеть сеть Хопфилда «фильтрует» входные данные, возвращаясь к устойчивому состоянию и, таким образом, позволяет решать задачи компрессии данных и построения ассоциативной памяти[13]. Частным случаем рекуррентных сетей является двунаправленные сети. В таких сетях между слоями существуют связи как в направлении от входного слоя к выходному, так и в обратном. Классическим примером является Нейронная сеть Коско.
Радиально-базисные функции
Искусственные нейронные сети, использующие в качестве активационных функций радиально-базисные (такие сети сокращённо называются RBF-сетями). Общий вид радиально-базисной функции:
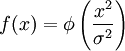 , например,
, например, 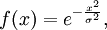
где x — вектор входных сигналов нейрона, σ — ширина окна функции, φ(y) — убывающая функция (чаще всего, равная нулю вне некоторого отрезка).
Радиально-базисная сеть характеризуется тремя особенностями:
1. Единственный скрытый слой
2. Только нейроны скрытого слоя имеют нелинейную активационную функцию
3. Синаптические веса связей входного и скрытого слоев равны единице
Про процедуру обучения — см. литературу
Самоорганизующиеся карты
Такие сети представляют собой соревновательную нейронную сеть с обучением без учителя, выполняющую задачу визуализации и кластеризации. Является методом проецирования многомерного пространства в пространство с более низкой размерностью (чаще всего, двумерное), применяется также для решения задач моделирования, прогнозирования и др. Является одной из версий нейронных сетей Кохонена.[14] Самоорганизующиеся карты Кохонена служат, в первую очередь, для визуализации и первоначального («разведывательного») анализа данных.[15]
Сигнал в сеть Кохонена поступает сразу на все нейроны, веса соответствующих синапсов интерпретируются как координаты положения узла, и выходной сигнал формируется по принципу «победитель забирает всё» — то есть ненулевой выходной сигнал имеет нейрон, ближайший (в смысле весов синапсов) к подаваемому на вход объекту. В процессе обучения веса синапсов настраиваются таким образом, чтобы узлы решетки «располагались» в местах локальных сгущений данных, то есть описывали кластерную структуру облака данных, с другой стороны, связи между нейронами соответствуют отношениям соседства между соответствующими кластерами в пространстве признаков.
Удобно рассматривать такие карты как двумерные сетки узлов, размещенных в многомерном пространстве. Изначально самоорганизующаяся карта представляет из себя сетку из узлов, соединенный между собой связями. Кохонен рассматривал два варианта соединения узлов — в прямоугольную и гексагональную сетку — отличие состоит в том, что в прямоугольной сетке каждый узел соединен с 4-мя соседними, а в гексагональной — с 6-ю ближайщими узлами. Для двух таких сеток процесс построения сети Кохонена отличается лишь в том месте, где перебираются ближайшие к данному узлу соседи.
Начальное вложение сетки в пространство данных выбирается произвольным образом. В авторском пакете SOM_PAK предлагаются варианты случайного начального расположения узлов в пространстве и вариант расположения узлов в плоскости. После этого узлы начинают перемещаться в пространстве согласно следующему алгоритму:
- Случайным образом выбирается точка данных x.
- Определяется ближайший к x узел карты (BMU — Best Matching Unit).
- Этот узел перемещается на заданный шаг по направлению к x. Однако, он перемещается не один, а увлекает за собой определенное количество ближайших узлов из некоторой окрестности на карте. Из всех двигающихся узлов наиболее сильно смещается центральный — ближайший к точке данных — узел, а остальные испытывают тем меньшие смещения, чем дальше они от BMU. В настройке карты различают два этапа — этап грубой (ordering) и этап тонкой (fine-tuning) настройки. На первом этапе выбираются большие значения окрестностей и движение узлов носит коллективный характер — в результате карта «расправляется» и грубым образом отражает структуру данных; на этапе тонкой настройки радиус окрестности равен 1-2 и настраиваются уже индивидуальные положения узлов. Кроме этого, величина смещения равномерно затухает со временем, то есть она велика в начале каждого из этапов обучения и близка к нулю в конце.
- Алгоритм повторяется определенное число эпох (понятно, что число шагов может сильно изменяться в зависимости от задачи).
Известные типы сетей
- Персептрон Розенблатта;
- Многослойный перцептрон;
- Сеть Джордана;
- Сеть Элмана;
- Сеть Хэмминга;
- Сеть Ворда;
- Сеть Хопфилда;
- Сеть Кохонена;
- Когнитрон;
- Неокогнитрон;
- Хаотическая нейронная сеть;
- Осцилляторная нейронная сеть;
- Сеть встречного распространения;
- Сеть радиальных базисных функций (RBF-сеть);
- Сеть обобщенной регрессии;
- Вероятностная сеть;
- Сиамская нейронная сеть;
- Сети адаптивного резонанса.
Отличия от машин с архитектурой фон Неймана
Длительный период эволюции придал мозгу человека много качеств, которые отсутствуют в машинах с архитектурой фон Неймана:
- Массовый параллелизм;
- Распределённое представление информации и вычисления;
- Способность к обучению и обобщению;
- Адаптивность;
- Свойство контекстуальной обработки информации;
- Толерантность к ошибкам;
- Низкое энергопотребление.
Нейронные сети — универсальные аппроксиматоры
Нейронные сети — универсальные аппроксимирующие устройства и могут с любой точностью имитировать любой непрерывный автомат. Доказана обобщённая аппроксимационная теорема[16]: с помощью линейных операций и каскадного соединения можно из произвольного нелинейного элемента получить устройство, вычисляющее любую непрерывную функцию с любой наперёд заданной точностью. Это означает, что нелинейная характеристика нейрона может быть произвольной: от сигмоидальной до произвольного волнового пакета или вейвлета, синуса или полинома. От выбора нелинейной функции может зависеть сложность конкретной сети, но с любой нелинейностью сеть остаётся универсальным аппроксиматором и при правильном выборе структуры может сколь угодно точно аппроксимировать функционирование любого непрерывного автомата.
Примеры приложений
Предсказание финансовых временных рядов
Входные данные — курс акций за год. Задача — определить завтрашний курс. Проводится следующее преобразование — выстраивается в ряд курс за сегодня, вчера, за позавчера, за позапозавчера. Следующий ряд — смещается по дате на один день и так далее. На полученном наборе обучается сеть с 3 входами и одним выходом — то есть выход: курс на дату, входы: курс на дату минус 1 день, минус 2 дня, минус 3 дня. Обученной сети подаем на вход курс за сегодня, вчера, позавчера и получаем ответ на завтра. Нетрудно заметить, что в этом случае сеть просто выведет зависимость одного параметра от трёх предыдущих. Если желательно учитывать ещё какой-то параметр (например, общий индекс по отрасли), то его надо добавить как вход (и включить в примеры), переобучить сеть и получить новые результаты. Для наиболее точного обучения стоит использовать метод ОРО, как наиболее предсказуемый и несложный в реализации.
Психодиагностика
Серия работ М. Г. Доррера с соавторами посвящена исследованию вопроса о возможности развития психологической интуиции у нейросетевых экспертных систем.[17][18] Полученные результаты дают подход к раскрытию механизма интуиции нейронных сетей, проявляющейся при решении ими психодиагностических задач. Создан нестандартный для компьютерных методик интуитивный подход к психодиагностике, заключающийся в исключении построения описанной реальности. Он позволяет сократить и упростить работу над психодиагностическими методиками.
Хемоинформатика
Нейронные сети широко используются в химических и биохимических исследованиях[19] В настоящее время нейронные сети являются одним из самых распространенных методов хемоинформатики для поиска количественных соотношений структура-свойство[20][21], благодаря чему они активно используются как для прогнозирования физико-химических свойств и биологической активности химических соединений, так и для направленного дизайна химических соединений и материалов с заранее заданными свойствами, в том числе при разработке новых лекарственных препаратов.
См. также
Примечания
- ↑ Мак-Каллок У. С., Питтс В.,Логическое исчисление идей, относящихся к нервной активности // В сб.: «Автоматы» под ред. К. Э. Шеннона и Дж. Маккарти. — М.: Изд-во иностр. лит., 1956. — с.363-384. (Перевод английской статьи 1943 г.)
- ↑ Pattern Recognition and Adaptive Control. BERNARD WIDROW
- ↑ Уидроу Б., Стирнс С., Адаптивная обработка сигналов. — М.: Радио и связь, 1989. — 440 c.
- ↑ Werbos P. J., Beyond regression: New tools for prediction and analysis in the behavioral sciences. Ph.D. thesis, Harvard University, Cambridge, MA, 1974.
- ↑ Галушкин А. И. Синтез многослойных систем распознавания образов. — М.: «Энергия», 1974.
- ↑ Rumelhart D.E., Hinton G.E., Williams R.J., Learning Internal Representations by Error Propagation. In: Parallel Distributed Processing, vol. 1, pp. 318—362. Cambridge, MA, MIT Press. 1986.
- ↑ Барцев С. И., Охонин В. А. Адаптивные сети обработки информации. Красноярск : Ин-т физики СО АН СССР, 1986. Препринт N 59Б. — 20 с.
- ↑ BaseGroup Labs — Практическое применение нейросетей в задачах классификации
- ↑ Такой вид кодирования иногда называют кодом «1 из N»
- ↑ 1 2 Открытые системы — введение в нейросети
- ↑ Миркес Е. М.,Логически прозрачные нейронные сети и производство явных знаний из данных, В кн.: Нейроинформатика / А. Н. Горбань, В. Л. Дунин-Барковский, А. Н. Кирдин и др. — Новосибирск: Наука. Сибирское предприятие РАН, 1998. — 296 с ISBN 5020314102
- ↑ Упоминание этой истории в журнале «Популярная механика»
- ↑ http://www.intuit.ru/department/expert/neuro/10/ INTUIT.ru — Рекуррентные сети как ассоциативные запоминающие устройства]
- ↑ Kohonen, T. (1989/1997/2001), Self-Organizing Maps, Berlin — New York: Springer-Verlag. First edition 1989, second edition 1997, third extended edition 2001, ISBN 0-387-51387-6, ISBN 3-540-67921-9
- ↑ Зиновьев А. Ю. Визуализация многомерных данных. — Красноярск: Изд. Красноярского государственного технического университета, 2000. — 180 с.
- ↑ Горбань А. Н., Обобщенная аппроксимационная теорема и вычислительные возможности нейронных сетей, Сибирский журнал вычислительной математики, 1998. Т.1, № 1. С. 12-24.
- ↑ Gorban A.N., Rossiyev D.A., Dorrer M.G., MultiNeuron — Neural Networks Simulator For Medical, Physiological, and Psychological Applications, Wcnn’95, Washington, D.C.: World Congress on Neural Networks 1995 International Neural Network Society Annual Meeting : Renaissance Hotel, Washington, D.C., USA, July 17-21, 1995.
- ↑ Доррер М. Г., Психологическая интуиция искусственных нейронных сетей, Дисс. ... 1998. Другие копии онлайн: [1], [2]
- ↑ Баскин И. И., Палюлин В. А., Зефиров Н. С., Применение искусственных нейронных сетей в химических и биохимических исследованиях, Вестн. Моск. Ун-Та. Сер. 2. Химия. 1999. Т.40. № 5.
- ↑ Гальберштам Н. М., Баскин И. И., Палюлин В. А., Зефиров Н. С. Нейронные сети как метод поиска зависимостей структура – свойство органических соединений // Успехи химии. — 2003. — Т. 72. — № 7. — С. 706-727.
- ↑ Баскин И. И., Палюлин В. А., Зефиров Н. С. Многослойные персептроны в исследовании зависимостей «структура-свойство» для органических соединений // Российский химический журнал (Журнал Российского химического общества им. Д.И.Менделеева). — 2006. — Т. 50. — С. 86-96.
Ссылки
- Artificial Neural Network for PHP 5.x - Серьезный проект по разработке нейронных сетей на языке программирования PHP 5.X
- Лекции по нейроинформатике
- Лекции по машинному обучению и нейронным сетям
- Форум, посвященный Нейронным Сетям и Генетическим Алгоритмам
- Форум по нейросетям на BaseGroup Labs
- Описание нейросетевых алгоритмов
- Миркес Е. М., Нейроинформатика: Учеб. пособие для студентов с программами для выполнения лабораторных работ.
- Forecasting Financial Markests using Artificial Neural Networks
- Пошаговые примеры реализации наиболее известных типов нейронных сетей на MATLAB, Neural Network Toolbox
- Лекции по нейронным сетям
- Подборка материалов по нейронным сетям и интеллектуальному анализу
- Статья противника применения нейронных сетей в прогнозировании цен на акции
- Подборка статей по нейронным сетям
- Программные проекты с использованием нейросетей
- Простой пример сети, с комментариями. Написан на php.
Литература
- Круглов Владимир Васильевич, Борисов Вадим Владимирович Искусственные нейронные сети. Теория и практика. — 1-е. — М.: Горячая линия - Телеком, 2001. — С. 382. — ISBN 5-93517-031-О
- В. А. Терехов, Д. В. Ефимов, И. Ю. Тюкин Нейросетевые системы управления. — 1-е. — Высшая школа, 2002. — С. 184. — ISBN 5-06-004094-1
- Уоссермен, Ф. Нейрокомпьютерная техника: Теория и практика = Neural Computing. Theory and Practice. — М.: Мир, 1992. — 240 с. — ISBN 5-03-002115-9
- Саймон Хайкин Нейронные сети: полный курс = Neural Networks: A Comprehensive Foundation. — 2-е. — М.: «Вильямс», 2006. — С. 1104. — ISBN 0-13-273350-1
- Роберт Каллан Основные концепции нейронных сетей = The Essence of Neural Networks First Edition. — 1-е. — «Вильямс», 2001. — С. 288. — ISBN 5-8459-0210-X
- Л.Н. Ясницкий Введение в искусственный интеллект. — 1-е. — Издательский центр "Академия", 2005. — С. 176. — ISBN 5-7695-1958-4
- Г. К. Вороновский, К. В. Махотило, С. Н. Петрашев, С. А. Сергеев Генетические алгоритмы, искусственные нейронные сети и проблемы виртуальной реальности. — заказное. — Х.: ОСНОВА, 1997. — С. 112. — ISBN 5-7768-0293-8
- Миркес Е. М., Нейрокомпьютер. Проект стандарта. — Новосибирск: Наука, 1999. — 337 с. ISBN 5-02-031409-9 Другие копии онлайн: [3], [4].
- Нейроинформатика. Новосибирск: Наука, 1998.
| Инженерия знаний | |
|---|---|
| Информатика | |
| Общие понятия | Данные · Метаданные · Знания · Метазнание · Представление знаний · База знаний · Онтология |
| Жёсткие модели | Продукции · Семантическая сеть · Фреймы · Логическая модель |
| Мягкие методы | Нейронная сеть · Генетический алгоритм · Нечёткая логика · Гибридная интеллектуальная система |
Wikimedia Foundation.2010.
