Генетический алгоритм | это... Что такое Генетический алгоритм? (original) (raw)

Генети́ческий алгори́тм (англ. genetic algorithm) — это эвристический алгоритм поиска, используемый для решения задач оптимизации и моделирования путём случайного подбора, комбинирования и вариации искомых параметров с использованием механизмов, напоминающих биологическую эволюцию. Является разновидностью эволюционных вычислений, с помощью которых решаются оптимизационные задачи с использованием методов естественной эволюции, таких как наследование, мутации, отбор и кроссинговер. Отличительной особенностью генетического алгоритма является акцент на использование оператора «скрещивания», который производит операцию рекомбинации решений-кандидатов, роль которой аналогична роли скрещивания в живой природе.

Содержание

История

Первые работы по симуляции эволюции были проведены в 1954 году Нильсом Баричелли на компьютере установленном в Институте Продвинутых Исследований Принстонского университета.[1][2] Его работа, опубликованная в том же году, привлекла широкое внимание общественности. С 1957 года,[3] австралийский генетик Алекс Фразер опубликовал серию работ по симуляции искусственного отбора среди организмов с множественным контролем измеримых характеристик. Положенное начало позволило компьютерной симуляции эволюционных процессов и методам, описанным в книгах Фразера и Барнелла(1970)[4] и Кросби (1973).[5], с 1960-х годов стать более распространенным видом деятельности среди биологов. Симуляции Фразера включали все важнейшие элементы современных генетических алгоритмов. Вдобавок к этому, Ганс-Иоахим Бремерманн в 1960-х опубликовал серию работ, которые также принимали подход использования популяции решений, подвергаемой рекомбинации, мутации и отбору, в проблемах оптимизации. Исследования Бремерманна также включали элементы современных генетических алгоритмов.[6] Среди прочих пионеров следует отметить Ричарда Фридберга, Джорджа Фридмана и Майкла Конрада. Множество ранних работ были переизданы Давидом Б. Фогелем (1998).[7]

Хотя Баричелли в своей работе 1963 года симулировал способности машины играть в простую игру,[8] искусственная эволюция стала общепризнанным методом оптимизации после работы Инго Рехенберга и Ханса-Пауля Швефеля в 1960-х и начале 1970-х годов двадцатого века – группа Рехенсберга смогла решить сложные инженерные проблемы согласно стратегиям эволюции.[9][10][11][12] Другим подходом была техника эволюционного программирования Лоренса Дж. Фогеля, которая была предложена для создания искусственного интеллекта. Эволюционное программирование первоначально использовавшее конечные автоматы для предсказывания обстоятельств, и использовавшее разнообразие и отбор для оптимизации логики предсказания. Генетические алгоритмы стали особенно популярны благодаря работе Джона Холланда в начале 70-х годов и его книге «Адаптация в естественных и искусственных системах» (1975)[13]. Его исследование основывалось на экспериментах с клеточными автоматами, проводившимися Холландом и на его трудах написанных в университете Мичигана. Холланд ввел формализованный подход для предсказывания качества следующего поколения, известный как Теорема схем. Исследования в области генетических алгоритмов оставались в основном теоретическими до середины 80-х годов, когда была наконец проведена Первая международная конференция по генетическим алгоритмам в Питтсбурге, Пенсильвания (США).

С ростом исследовательского интереса существенно выросла и вычислительная мощь настольных компьютеров, это позволило использовать новую вычислительную технику на практике. В конце 80-х, компания General Electric начала продажу первого в мире продукта, работавшего с использованием генетического алгоритма. Им стал набор промышленных вычислительных средств. В 1989, другая компания Axcelis, Inc. выпустила Evolver – первый в мире коммерческий продукт на генетическом алгоритме для настольных компьютеров. Журналист The New York Times в технологической сфере Джон Маркофф писал [14] об Evolver в 1990 году.

Описание алгоритма

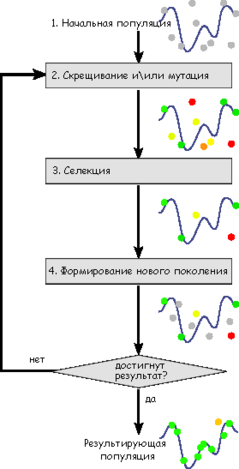
Схема работы генетического алгоритма

Задача формализуется таким образом, чтобы её решение могло быть закодировано в виде вектора («генотипа») генов, где каждый ген может быть битом, числом или неким другим объектом. В классических реализациях ГА предполагается, что генотип имеет фиксированную длину. Однако существуют вариации ГА, свободные от этого ограничения.

Некоторым, обычно случайным, образом создаётся множество генотипов начальной популяции. Они оцениваются с использованием «функции приспособленности», в результате чего с каждым генотипом ассоциируется определённое значение («приспособленность»), которое определяет насколько хорошо фенотип, им описываемый, решает поставленную задачу.

При выборе «функции приспособленности» (или fitness function в англоязычной литературе) важно следить, чтобы её «рельеф» был «гладким».

Из полученного множества решений («поколения») с учётом значения «приспособленности» выбираются решения (обычно лучшие особи имеют большую вероятность быть выбранными), к которым применяются «генетические операторы» (в большинстве случаев «скрещивание» — crossover и «мутация» — mutation), результатом чего является получение новых решений. Для них также вычисляется значение приспособленности, и затем производится отбор («селекция») лучших решений в следующее поколение.

Этот набор действий повторяется итеративно, так моделируется «эволюционный процесс», продолжающийся несколько жизненных циклов (поколений), пока не будет выполнен критерий остановки алгоритма. Таким критерием может быть:

Генетические алгоритмы служат, главным образом, для поиска решений в многомерных пространствах поиска.

Таким образом, можно выделить следующие этапы генетического алгоритма:

  1. Задать целевую функцию (приспособленности) для особей популяции
  2. Создать начальную популяцию
  1. Размножение (скрещивание)
  2. Мутирование
  3. Вычислить значение целевой функции для всех особей
  4. Формирование нового поколения (селекция)
  5. Если выполняются условия остановки, то (конец цикла), иначе (начало цикла).

Создание начальной популяции

Перед первым шагом нужно случайным образом создать начальную популяцию; даже если она окажется совершенно неконкурентоспособной, вероятно, что генетический алгоритм все равно достаточно быстро переведет ее в жизнеспособную популяцию. Таким образом, на первом шаге можно особенно не стараться сделать слишком уж приспособленных особей, достаточно, чтобы они соответствовали формату особей популяции, и на них можно было подсчитать функцию приспособленности (Fitness). Итогом первого шага является популяция H, состоящая из N особей.

Размножение (Скрещивание)

Размножение в генетических алгоритмах обычно половое — чтобы произвести потомка, нужны несколько родителей, обычно два.

Размножение в разных алгоритмах определяется по-разному — оно, конечно, зависит от представления данных. Главное требование к размножению — чтобы потомок или потомки имели возможность унаследовать черты обоих родителей, «смешав» их каким-либо способом.

Почему особи для размножения обычно выбираются из всей популяции H, а не из выживших на первом шаге элементов H0 (хотя последний вариант тоже имеет право на существование)? Дело в том, что главный бич многих генетических алгоритмов — недостаток разнообразия (diversity) в особях. Достаточно быстро выделяется один-единственный генотип, который представляет собой локальный максимум, а затем все элементы популяции проигрывают ему отбор, и вся популяция «забивается» копиями этой особи. Есть разные способы борьбы с таким нежелательным эффектом; один из них — выбор для размножения не самых приспособленных, но вообще всех особей.

Мутации

К мутациям относится все то же самое, что и к размножению: есть некоторая доля мутантов m, являющаяся параметром генетического алгоритма, и на шаге мутаций нужно выбрать mN особей, а затем изменить их в соответствии с заранее определёнными операциями мутации.

Отбор

На этапе отбора нужно из всей популяции выбрать определённую её долю, которая останется «в живых» на этом этапе эволюции. Есть разные способы проводить отбор. Вероятность выживания особи h должна зависеть от значения функции приспособленности Fitness(h). Сама доля выживших s обычно является параметром генетического алгоритма, и её просто задают заранее. По итогам отбора из N особей популяции H должны остаться sN особей, которые войдут в итоговую популяцию H'. Остальные особи погибают.

Критика

Существует несколько поводов для критики на счёт использования генетического алгоритма по сравнению с другими методами оптимизации:

Имеется много скептиков относительно целесообразности применения генетических алгоритмов. Например, Стивен С. Скиена, профессор кафедры вычислительной техники университета Стоуни—Брук, известный исследователь алгоритмов, лауреат премии института IEEE пишет[16]:

Применение генетических алгоритмов

Генетические алгоритмы применяются для решения следующих задач:

  1. Оптимизация функций
  2. Оптимизация запросов в базах данных
  3. Разнообразные задачи на графах (задача коммивояжера, раскраска, нахождение паросочетаний)
  4. Настройка и обучение искусственной нейронной сети
  5. Задачи компоновки
  6. Составление расписаний
  7. Игровые стратегии
  8. Теория приближений
  9. Искусственная жизнь
  10. Биоинформатика (фолдинг белков)

Пример тривиальной реализации на C++

Поиск в одномерном пространстве, без скрещивания.

#include #include #include #include #include

int main() { ::std::srand((unsigned int)::std::time(NULL)); const size_t N = 1000; int a[N] = { 0 }; for ( ; ; ) { //мутация в случайную сторону каждого элемента: for ( size_t i = 0 ; i < N ; ++i ) if ( ::std::rand() % 2 == 1 ) a[i] += 1; else a[i] -= 1; //теперь выбираем лучших, отсортировав по возрастанию... ::std::sort(a, a+N); //... и тогда лучшие окажутся во второй половине массива. //скопируем лучших в первую половину, куда они оставили потомство, а первые умерли: ::std::copy(a+N/2, a+N, a); //теперь посмотрим на среднее состояние популяции. Как видим, оно всё лучше и лучше. ::std::cout << ::std::accumulate(a, a+N, 0) / N << ::std::endl; } }

Примечания

  1. ↑ Barricelli, Nils Aall (1954). «Esempi numerici di processi di evoluzione». Methodos: 45–68.
  2. ↑ Barricelli, Nils Aall (1957). «Symbiogenetic evolution processes realized by artificial methods». Methodos: 143–182.
  3. ↑ Fraser, Alex (1957). «Simulation of genetic systems by automatic digital computers. I. Introduction». Aust. J. Biol. Sci. 10: 484–491.
  4. ↑ Fraser Alex Computer Models in Genetics. — New York: McGraw-Hill, 1970. — ISBN 0-07-021904-4
  5. ↑ Crosby Jack L. Computer Simulation in Genetics. — London: John Wiley & Sons, 1973. — ISBN 0-471-18880-8
  6. ↑ 02.27.96 - UC Berkeley's Hans Bremermann, professor emeritus and pioneer in mathematical biology, has died at 69
  7. ↑ Fogel David B. (editor) Evolutionary Computation: The Fossil Record. — New York: IEEE Press, 1998. — ISBN 0-7803-3481-7
  8. ↑ Barricelli, Nils Aall (1963). «Numerical testing of evolution theories. Part II. Preliminary tests of performance, symbiogenesis and terrestrial life». Acta Biotheoretica (16): 99–126.
  9. ↑ Rechenberg Ingo Evolutionsstrategie. — Holzmann-Froboog, 1973. — ISBN 3-7728-0373-3
  10. ↑ Schwefel Hans-Paul Numerische Optimierung von Computer-Modellen (PhD thesis). — 1974.
  11. ↑ Schwefel Hans-Paul Numerische Optimierung von Computor-Modellen mittels der Evolutionsstrategie : mit einer vergleichenden Einführung in die Hill-Climbing- und Zufallsstrategie. — Birkhäuser, 1977. — ISBN 3-7643-0876-1
  12. ↑ Schwefel Hans-Paul Numerical optimization of computer models (Translation of 1977 Numerische Optimierung von Computor-Modellen mittels der Evolutionsstrategie. — Wiley, 1981. — ISBN 0-471-09988-0
  13. ↑ J. H. Holland. Adaptation in natural and artificial systems. University of Michigan Press, Ann Arbor, 1975.
  14. ↑ Markoff, John. What's the Best Answer? It's Survival of the Fittest, New York Times (29 августа 1990). Проверено 9 августа 2009.
  15. ↑ Wolpert, D.H., Macready, W.G., 1995. No Free Lunch Theorems for Optimisation. Santa Fe Institute, SFI-TR-05-010, Santa Fe.
  16. ↑ Steven S. Skiena. The Algorithm Design Manual. Second Edition. Springer, 2008.

Книги

Ссылки

Просмотр этого шаблона Методы оптимизации
Одномерные Метод золотого сечения • Дихотомия • Метод парабол • Перебор по сетке • Метод Фибоначчи • Троичный поиск
Прямые методы Метод Гаусса • Метод Нелдера — Мида • Метод Хука — Дживса • Метод конфигураций • Метод Розенброка
Первого порядка Градиентный спуск • Метод Зойтендейка • Покоординатный спуск • Метод сопряжённых градиентов • Квазиньютоновские методы • Алгоритм Левенберга — Марквардта
Второго порядка Метод Ньютона • Метод Ньютона — Рафсона
Стохастические Метод Монте-Карло • Имитация отжига • Эволюционные алгоритмы • Дифференциальная эволюция • Муравьиный алгоритм • Метод роя частиц
Методы линейного программирования Симплекс-метод • Алгоритм Гомори • Метод эллипсоидов • Метод потенциалов
Методы нелинейногопрограммирования Последовательное квадратичное программирование
Просмотр этого шаблона Искусственный интеллект
Философия Тест Тьюринга • Китайская комната Nuvola apps Talk.PNG Портал
Направления Агентный подход • Адаптивное управление • Инженерия знаний • Модель жизнеспособной системы • Машинное обучение • Нейронные сети • Нечёткая логика • Обработка естественного языка • Распознавание образов • Роевой интеллект • Эволюционные алгоритмы • Экспертная система
Применение Голосовое управление • Задача классификации • Классификация документов • Кластеризация документов • Кластерный анализ • Локальный поиск • Машинный перевод • Оптическое распознавание символов • Распознавание речи • Распознавание рукописного ввода • Игровой ИИ
Исследователи Норберт Винер • Алан Тьюринг • В. М. Глушков • Г. С. Осипов • Д. Э. Попов • Д. А. Поспелов • М. Г. Гаазе-Рапопорт • Т. А. Гаврилова • В. Ф. Хорошевский • Г. С. Поспелов • Марвин Мински • Джон Маккарти • Фрэнк Розенблатт • Чарльз Бэббидж • Аллен Ньюэлл • Герберт Саймон • Ноам Хомский • Джуда Перл • Сеймур Паперт • Клод Шеннон • Джозеф Уайзенбаум • Патрик Винстон • В. К. Финн
Организации Государственный университет информатики и искусственного интеллекта • Singularity Institute for Artificial Intelligence