Прямое произведение множеств | это... Что такое Прямое произведение множеств? (original) (raw)

Прямое или декартово произведение множеств — множество, элементами которого являются всевозможные упорядоченные пары элементов исходных двух множеств. Данное понятие употребляется не только в теории множеств, но также в алгебре, топологии и прочих разделах математики благодаря тому, что прямое произведение часто наследует структуры (алгебраические, топологические и т. д.), существующие на перемножаемых множествах.

Содержание

1 Прямое произведение в теории множеств
2 Прямое произведение отображений
3 Воздействие на математические структуры
4 Вариации и обобщения
5 См. также

Прямое произведение в теории множеств

Произведение двух множеств

| | | | | | | | | | | ---------------------------------------------------------- | - | - | - | - | - | - | - | | в | в | в | в | в | в | в | в | | и | и | и | и | и | и | и | и | | к | к | к | к | к | к | к | к | | Произведение множества {в, и, к}на множество цветов радуги | | | | | | | |

Пусть дано два множества X и Y. Прямое произведение 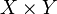$X\times Y$ множества X и множества Y есть такое множество 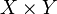$X \times Y$ , элементами которого являются упорядоченные пары (x,y) для всевозможных $x\in X$ и $y\in Y$ .

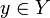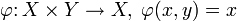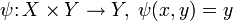Отображения произведения множеств в его множители ( $\varphi\colon X\times Y\to X,\; \varphi(x,y)=x$ и $\psi\colon X\times Y\to Y,\; \psi(x,y)=y$ ) называют координатными функциями.

Аналогично строятся произведения нескольких множеств.

Декартова степень

000	001	002	010	011	012	020	021	022
100	101	102	110	111	112	120	121	122
200	201	202	210	211	212	220	221	222
{0, 1, 2}3, 33 = 27 элементов

_n_-я Декартова степень множества X определяется для целых неотрицательных n, как _n_-кратное Декартово произведение X на себя:

$\begin{matrix} X^n = & \underbrace{X\times X\times \ldots \times X}. \\ & n \end{matrix}$

При положительных n Декартова степень X n состоит из всех упорядоченных наборов (кортежей) элементов из X длины n.

При n = 0, Декартова степень _X_0 по определению содержит единственный элемент — пустой кортеж.

Прямое произведение семейства множеств

Дальнейшее обобщение понятия прямого произведения приводит к произведениям по индексному множеству I (возможно, бесконечному): X = Π_X_ i, элементы которого сопоставляют каждому индексу i из I элемент множества X i.

Прямое произведение отображений

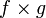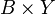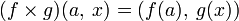Пусть f — отображение из A в B, а g — отображение из X в Y. Их прямым произведением $f\times g$ называется отображение из $A\times X$ в $B\times Y$ : $(f\times g)(a,\; x) = (f(a),\; g(x))$ .

Аналогично вышеизложенному, данное определение обобщается на многократные и бесконечные произведения.

Воздействие на математические структуры

Прямое произведение групп

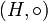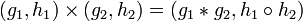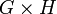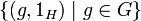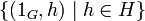Прямое (декартово) произведение двух групп (G, * ) и $(H,\circ)$ — это группа из всех пар элементов (g,h) с операцией поэлементного умножения: $(g_1,h_1)\times(g_2,h_2)=(g_1*g_2,h_1\circ h_2)$ . Эта группа обозначается как $G\times H$ . Сомножители G и H изоморфны двум нормальным подгруппам своего произведения, $\{(g,1_H)\mid g\in G\}$ и $\{(1_G,h)\mid h\in H\}$ соответственно. Пересечение этих подгрупп состоит из одного элемента (1_G_,1_H_), который является единицей группы-произведения. Координатные функции произведения групп являются гомоморфизмами.

Это определение распространяется на произвольное конечное число перемножаемых групп; ассоциативность декартова произведения следует из ассоциативности операций перемножаемых групп.

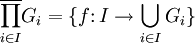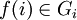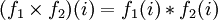Однако, для бесконечного числа перемножаемых групп понятия декартового и прямого произведения принято различать. В общем случае, $\overline{\prod_{i\in I}} G_i=\{f\colon I\to\bigcup_{i\in I} G_i\}$ , где $f(i)\isin G_i$ и $(f_1\times f_2)(i)=f_1(i)*f_2(i)$ . (Операция в правой части — это операция группы G i.) Единицей группы-произведения будет последовательность, составленная из единиц всех перемножаемых групп: 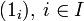$(1_i),\; i\in I$ . Например, для счётного числа групп: 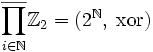$\overline{\prod_{i\in\mathbb{N}}} \mathbb{Z}_2=(2^\mathbb{N},\; \operatorname{xor})$ , где в правой части стоит множество всех бесконечных двоичных последовательностей.

Подгруппа на множестве всех f, носитель которых (то есть множество 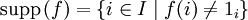$\mathrm{supp}\,(f) = \{i\in I\mid f(i)\ne 1_i\}$ ) конечен, называется прямым произведением. Например, прямое произведение того же самого набора множеств $\prod_{i\in\mathbb{N}} \mathbb{Z}_2\ =\ (\mathbb{N},\; \operatorname{xor})$ содержит все двоичные последовательности с конечным числом единиц, а их можно трактовать как двоичные представления натуральных чисел.

Прямое произведение других алгебраических структур

Аналогично произведению групп, можно определить произведения колец, алгебр, модулей и линейных пространств, причём в определении прямого произведения 1_i_ (см. выше) следует заменить нулём. Однако, как правило, произведения этих структур называют прямой суммой.

Прямое произведение топологических пространств

Пусть X и Y — два топологических пространства. Топология произведения 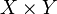$X\times Y$ задаётся базой, состоящей из всевозможных произведений 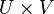$U\times V$ , где U — открытое подмножество X и V — открытое подмножество Y.

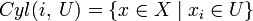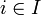Определение легко обобщается на случай произведения нескольких пространств. Для бесконечного произведения X = Π_X_ i определение усложняется. Определим открытый цилиндр $Cyl(i,\;U) = \{x\in X\mid x_i\in U\}$ , где $i\in I$ и U — открытое подмножество X i.

Топология бесконечного произведения будет задаваться базой, составленной из всевозможных пересечений конечного числа открытых цилиндров (такая топология аналогична компактно-открытой топологии пространств отображений если считать индексное множество I имеющим дискретную топологию).

Теорема Тихонова утверждает компактность произведений любого количества компактных пространств; однако для бесконечных произведений её не удаётся доказать без использования аксиомы выбора (или равносильных ей утверждений теории множеств).

Также, теорема Александрова показывает, что любое топологическое пространство можно вложить в (бесконечное) произведение связных двоеточий, если только выполнена аксиома Колмогорова (а иные пространства и не рассматриваются).

Прямое произведение графов

| | — |  | | | ----- | -- | - | |  | — |  | |  |  |  | |  | — |  |

Множество вершин прямого произведения двух графов G и H задаётся как произведение вершин графов сомножителей. Рёбрами будут соединены следующие па́ры вершин:

Иначе говоря, множество рёбер произведения графов является объединением двух произведений: рёбер первого на вершины второго, и вершин первого на рёбра второго.

Вариации и обобщения

Дальнейшее развитие идея прямого произведения получила в теории категорий, где она послужила основой для понятия произведения объектов. Неформально, произведение двух объектов A и B — это наиболее общий объект в данной категории, для которого существуют проекции на A и B. Во многих категориях (множеств, групп, графов, …) произведением объектов является именно их прямое произведение. Важно, что в большинстве случаев важно не столько конкретное определение прямого произведения, сколько указанное выше свойство универсальности. Различные определения будут давать при этом изоморфные объекты.

См. также

Wikimedia Foundation.2010.