P-адическое число | это... Что такое P-адическое число? (original) (raw)

_p_-ади́ческое число (произносится: пэ-адическое) — элемент расширения поля рациональных чисел, являющегося пополнением поля рациональных чисел относительно _p_-адической нормы, которая определяется на основе свойств делимости целых чисел на заданное простое число р.

_p_-адические числа были введены Гензелем (нем.) в 1897 году [1].

Поле _p_-адических чисел обычно обозначается 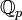$\mathbb Q_p$ или $\mathbf Q_p$ .

Содержание

1 Алгебраическое построение
- 1.1 Целые p-адические числа
  * 1.1.1 Стандартное определение
  * 1.1.2 Определение через проективный предел
  * 1.1.3 Свойства
- 1.2 p-адические числа
  * 1.2.1 Определение как поля частных
  * 1.2.2 Свойства
2 Метрическое построение
3 Свойства
4 Применения
5 Литература
6 Ссылки

Алгебраическое построение

Целые _p_-адические числа

Стандартное определение

Целым _p_-адическим числом для произвольного простого p называется бесконечная последовательность 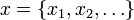$x=\{x_1,x_2,\ldots\}$ вычетов x n по модулю p n, удовлетворяющих условию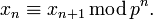 $x_n\equiv x_{n+1}\,\mathrm{mod}\,{p^n}.$

Сложение и умножение целых _p_-адических чисел определяется как почленное сложение и умножение таких последовательностей. Для них непосредственно проверяются все аксиомы кольца.

Определение через проективный предел

В терминах проективных пределов кольцо целых _p_-адических чисел определяется как предел

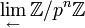
$\lim_{\leftarrow}\Bbb{Z} / {p^n}\Bbb{Z}$

колец 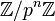$\Bbb{Z} / {p^n}\Bbb{Z}$ вычетов по модулю p n относительно естественных проекций $\Bbb{Z}/{p^{n+1}}\Bbb{Z} \to \Bbb{Z}/{p^n}\Bbb{Z}$ .

Эти рассмотрения можно провести в случае не только простого числа p, но и любого составного числа m — получится т. н. кольцо _m_-адических чисел, но это кольцо в отличие от 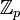$\Bbb{Z}_p$ обладает делителями нуля, поэтому дальнейшие построения, рассматриваемые ниже, к нему неприменимы.

Свойства

Обычные целые числа вкладываются в кольцо _p_-адических чисел очевидным образом: x = {x,x,...} и являются подкольцом.

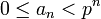Беря в качестве элемента класса вычетов число $x_n\equiv a_n\,\operatorname{mod}\,{p^n}.$ , такое, что $0\le a_n<p^n$ , мы можем записать каждое целое _p_- адическое число в виде x = {_a_1,_a_2,...} однозначным образом. Такой вид называется каноническим. 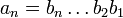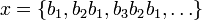Записывая каждое an в _p_-ичной системе счисления $a_n=b_n\ldots b_2b_1$ и учитывая что $a_n\equiv a_{n+1}\,\mathrm{mod}\,{p^n}.$ мы можем всякое _p_-адическое число в каноническом виде представить в виде $x=\{b_1, b_2b_1, b_3b_2b_1,\ldots\}$ или записывая в виде бесконечной последовательности цифр в _p_-ичной системе счисления 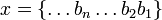$x=\{\ldots b_n\ldots b_2b_1\}$ . Действия над такими последовательностями производятся по обыкновенными правилами сложения, вычитания и умножения «столбиком» в _p_-ичной системе счисления (в нашем примере _p_=5).

P adic arithm.gif

В такой форме записи натуральным числам и нулю соответствуют _p_-адические числа с конечным числом ненулевых цифр, точно таких, как у исходного числа. Отрицательным числам соответствуют _p_-адические числа с бесконечным числом ненулевых цифр, например в пятеричной системе −1=…4444=(4).

Кольцо целых _p_-адических чисел обычно обозначается 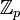$\Bbb{Z}_p$ .

_p_-адические числа

Определение как поля частных

_p_-адическим числом называется элемент поля частных 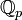$\Bbb{Q}_p$ кольца 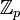$\Bbb{Z}_p$ целых _p_-адических чисел. Это поле называется полем _p_-адических чисел.

Свойства

Поле _p_-адических чисел содержит в себе поле рациональных чисел. Нетрудно доказать, что любое целое _p_-адическое число, не кратное p обратимо в кольце 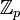$\Bbb{Z}_p$ , а кратное p однозначно записывается в виде x p n, где x не кратно p и поэтому обратимо, а n > 0, то ясно, что любой ненулевой элемент поля 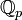$\Bbb{Q}_p$ может быть записан в виде x p n, где x не кратно p а n любое, если n отрицательно, то исходя из представления целых _p_-адических чисел в виде последовательности цифр в _p_-ичной системе счисления мы можем записать любое такое _p_-адическое число в виде последовательности 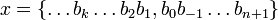$x=\{\ldots b_k\ldots b_2b_1,b_0b_{-1}\ldots b_{n+1}\}$ , то есть формально в виде в виде _p_-ичной дроби с конечным числом цифр после запятой и, возможно, бесконечным числом ненулевых цифр до запятой. Деление таких чисел можно также производить аналогично «школьному» правилу, но начиная с младших, а не старших разрядов числа. Так, в той же пятеричной системе имеем:

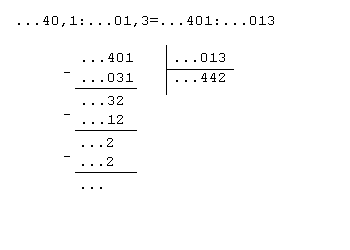
P adic division.gif

Метрическое построение

Любое рациональное число r можно представить как $r=p^n\frac ab$ где a и b целые числа, не делящиеся на p, а n — целое. Тогда | r | p — _p_-адическая норма r — определяется как p − n. Если r = 0, то | r | p = 0.

Поле _p_-адических чисел есть пополнение поля рациональных чисел с метрикой d p, определённой _p_-адической нормой: d p(x,y) = | x − y | p. Это построение аналогично построению поля вещественных чисел как пополнения поля рациональных чисел при помощи нормы, являющейся обычной абсолютной величиной.

Норма | r | p продолжается по непрерывности до нормы на 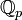$\Bbb{Q}_p$ .

Свойства

Каждый элемент _x_-поля _p_-адических чисел может быть представлен в виде сходящегося ряда

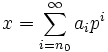
$x=\sum_{i=n_0}^\infty a_ip^i$

где _n_0 — некоторое целое число, а a i — целые неотрицательные числа, не превосходящие p − 1, а именно взяв в качестве a i цифры из записи _p_-адического числа x в виде последовательности цифр в системе счисления с основанием p. Такая сумма всегда сходится в метрике d p к самому x.

p-адическая норма | x | p удовлетворяет сильному неравенству треугольника

$|x-z|_p\le\max\{|x-y|_p,|y-z|_p\}.$

метрическое пространство 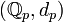$(\Bbb{Q}_p,d_p)$ гомеоморфно Канторову множеству, а пространство 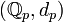$(\Bbb{Q}_p,d_p)$ гомеоморфно Канторову множеству с вырезанной точкой.
Для различных p нормы | x | p независимы, а поля 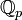$\Bbb{Q}_p$ неизоморфны.
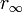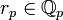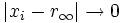Для любых элементов $r_\infty$ , _r_2, _r_3, _r_5, _r_7, …, таких что $r_\infty \in \Bbb R$ и $r_p\in \Bbb Q_p$ , можно найти последовательность рациональных чисел x n, таких что для любого p, $|x_i-r_p|_p\to 0$ и $|x_i-r_\infty|\to 0$ .

Применения

Если 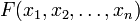$F(x_1,x_2,\ldots,x_n)$ — многочлен с целыми коэффициентами, то разрешимость при всех k сравнения

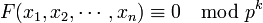
$F(x_1,x_2,\cdots,x_n)\equiv 0 \mod p^k$

эквивалентна разрешимости уравнения

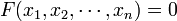
$F(x_1,x_2,\cdots,x_n) = 0$

в целых _p_-адических числах. Необходимым условием разрешимости этого уравнения в целых или рациональных числах является его разрешимость в кольцах или, соответственно, полях _p_-адических чисел при всех p, а также в поле вещественных чисел. Для некоторых классов многочленов (например, для квадратичных форм) это условие является также достаточным.

На практике для проверки разрешимости уравнения в целых _p_-адических числах достаточно проверить разрешимость указанного сравнения для определенного конечного числа значений k. Например, согласно лемме Гензеля (Hensel’s lemma), при n = 1 достаточным условием для разрешимости сравнения при всех натуральных k служит наличие простого решения у сравнения по модулю p (то есть простого корня у соответствующего уравнения в поле вычетов по модулю p). Иначе говоря, при n = 1 для проверки наличия корня у уравнения в целых _p_-адических числах, как правило, достаточно решить соответствующее сравнение при k = 1.

Литература

Боревич З. И., Шафаревич И. Р. Теория чисел, — М.: Наука, 1985.
Коблиц Н. р-адические числа, р-адический анализ и дзета-функции, — М.: Мир, 1982.
Серр Ж.-П. Курс арифметики, — М.: Мир, 1972.
Б. Беккер, С. Востоков, Ю. Ионин 2-адические числа // Квант. — 1979. — Т. 2. — С. 26—31.
_p_-адические числа для «чайников»

Ссылки

↑ Kurt Hensel Über eine neue Begründung der Theorie der algebraischen Zahlen // Jahresbericht der Deutschen Mathematiker-Vereinigung. — 1897. — Т. 6. — № 3. — С. 83—88.(нем.)

Числа
Простые	натуральные \| целые	рациональные	иррациональные	вещественные	p-адические	алгебраические	трансцендентные
Составные	комплексные \| дуальные	двойные	кватернионы	числа Кэли (октавы)	седенионы	гиперкомплексные