Дуальный базис | это... Что такое Дуальный базис? (original) (raw)

Те́нзор — объект линейной алгебры. Частными случаями тензоров являются скаляры, векторы и билинейные формы.

Часто тензор представляют как многомерную таблицу $d\times d\times \cdots \times d$ (где d — размерность векторного пространства, над которым задан тензор, а число сомножителей совпадает с «валентностью тензора»), заполненную числами (компонентами тензора).

Такое представление (за исключением тензоров валентности ноль — скаляров) возможно только после выбора базиса (или системы координат), при смене базиса компоненты тензора меняются определённым образом. При этом сам тензор как «геометрическая сущность» от выбора базиса не зависит. Это можно увидеть на примере вектора, являющегося частным случаем тензора: компоненты вектора меняются при смене координатных осей, но сам вектор — наглядным образом которого может быть просто нарисованная стрелка — от этого не изменяется.

Термин «тензор» также зачастую служит сокращением для термина «тензорное поле», изучением которых занимается тензорное исчисление.

Определения

Современное определение

Тензор ранга (n,m) над _d_-мерным векторным пространством V есть элемент тензорного произведения m пространств V и n сопряжённых пространств V * (то есть пространств линейных функционалов (1-форм) на V)

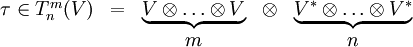
$\begin{matrix} \tau \in T^m_n(V) & = & \underbrace{ V\otimes \ldots \otimes V} & \otimes & \underbrace{ V^*\otimes \ldots \otimes V^*} \\ & & m & & n \end{matrix}$

Сумма чисел n + m называется валентностью тензора (её также часто называют рангом). Тензор ранга (n,m) также называется n раз ковариантным и m раз контравариантным.

NB часто термином ранг пользуются как синонимом определённого здесь термина валентность. Также бывает и обратное, то есть использование термина валентность в значении ранг, определённом здесь.

Тензор как полилинейная функция

Точно так же как ковариантный тензор ранга (1,0) можно представлять как линейный функционал, тензор τ ранга (n,0) удобно представлять себе как функцию 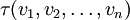$\tau(v_1,v_2,\ldots,v_n)$ от n векторных аргументов 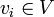$v_i\in V$ , которая линейна по каждому аргументу v i (такие функции называются полилинейными), то есть для любой константы c из поля F (над которым определено векторное пространство)

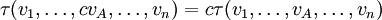
$\tau(v_1,\ldots,cv_A,\ldots,v_n)=c\tau(v_1,\ldots,v_A,\ldots,v_n)$

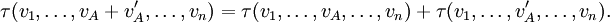
$\tau(v_1,\ldots,v_A+v_A',\ldots,v_n)=\tau(v_1,\ldots,v_A,\ldots,v_n)+\tau(v_1,\ldots,v_A',\ldots,v_n).$

В том же ключе, тензор τ произвольного ранга (n,m) представляется полилинейным функционалом от n векторов и m ковекторов:

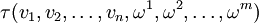
$\tau(v_1,v_2,\ldots,v_n,\omega^1,\omega^2,\ldots,\omega^m)$

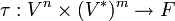
$\tau:V^n\times (V^*)^m \to F$

Компоненты тензора

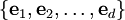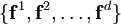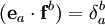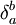Выберем в пространстве V базис $\{\mathbf{e}_1,\mathbf{e}_2,\ldots,\mathbf{e}_d\}$ , и соответственно $\{\mathbf{f}^1,\mathbf{f}^2,\ldots,\mathbf{f}^d\}$ — дуальный базис в сопряженном пространстве V * (то есть $(\mathbf{e}_a \cdot \mathbf{f}^b) = \delta_a^b$ , где $\delta_a^b$ — символ Кронекера).

Тогда в тензорном произведении 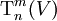$\Tau^m_n(V)$ пространств 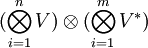$(\bigotimes_{i=1}^n V) \otimes (\bigotimes_{i=1}^m V^*)$ естественным образом возникает базис

$\{ \mathbf{e}_{i_1}\,\otimes\,\mathbf{e}_{i_2}\,\otimes\,\ldots\,\otimes\,\mathbf{e}_{i_n}\,\otimes\,\mathbf{f}^{j_1}\,\otimes\,\mathbf{f}^{j_2}\,\otimes\,\ldots\,\otimes\,\mathbf{f}^{j_m}\},\quad 1\leqslant i_a,j_b \leqslant d$ .

Если определить тензор как полилинейную функцию, то его компоненты определяются значениями этой функции на базисе 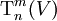$\Tau^m_n(V)$ :

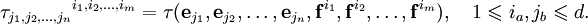
${\tau_{j_1,j_2,\ldots,j_n}}^{i_1,i_2,\ldots,i_m} = \tau( \mathbf{e}_{j_1},\mathbf{e}_{j_2},\ldots,\mathbf{e}_{j_n}, \mathbf{f}^{i_1},\mathbf{f}^{i_2},\ldots,\mathbf{f}^{i_m} ),\quad 1\leqslant i_a, j_b \leqslant d.$

После этого тензор можно записать как линейную комбинацию базисных тензорных произведений:

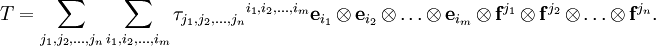
$T = \sum_{j_1,j_2,\ldots,j_n}^{} \sum_{i_1,i_2,\ldots,i_m}^{} {\tau_{j_1,j_2,\ldots,j_n}}^{i_1,i_2,\ldots,i_m} \mathbf{e}_{i_1}\,\otimes\,\mathbf{e}_{i_2}\,\otimes\,\ldots\,\otimes\,\mathbf{e}_{i_m}\,\otimes\,\mathbf{f}^{j_1}\,\otimes\,\mathbf{f}^{j_2}\,\otimes\,\ldots\,\otimes\,\mathbf{f}^{j_n}.$

Нижние индексы компонент тензора называются ковариантными, а верхние — контравариантными. Например, разложение некоторого дважды ковариантного тензора h будет таким:

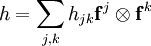
$h = \sum_{j,k} h_{jk} \mathbf{f}^j \otimes \mathbf{f}^k$

О классическом определении

Классический подход к определению тензора, более распространённый в физической литературе, начинает с представления тензоров в компонентах. Тензор определяется как геометрический объект, который описывается многомерным массивом, то есть набором чисел, занумерованных несколькими индексами, или, иначе говоря, таблицей (вообще говоря, _n_-мерной, где n — валентность тензора (см. выше)).

Так вектор (тензор первого ранга) задаётся одномерным массивом (строкой или лучше — столбцом), а такие объекты как линейный оператор и квадратичная форма — двумерной матрицей. Скаляр же (тензор нулевого ранга) задаётся одним числом (которое можно рассматривать как нульмерный массив с единственным элементом). (Скаляры и векторы удобно рассматривать в качестве частных случаев тензоров, так как все тензорные определения и теоремы для них в силе и векторы со скалярами можно при общем рассмотрении не упоминать отдельно).

Вводятся тензорные операции, которые можно считать прямым обобщением матричных операций (умножение матриц между собой и с векторами), а также векторных операций, таких, как скалярное произведение. Эти операции, если исходить из современного (аксиоматического) определения, прямо вытекают из (поли-)линейности тензоров в этом определении, после разложения векторов, свёртываемых с тензорами, по базису векторного пространства, точно так же, как и матричные операции вытекают из линейности линейных операторов и билинейных форм, представлением каждого из которых в конкретном базисе является конкретная матрица.

С помощью этих операций тензоры связываются с такими фундаментальными геометрическими объектами, как векторы и скаляры, чем, в конечном счёте, определяется их геометрический смысл. Эти же операции связывают тензоры с матрицами преобразований координат (матрицами якоби). Если речь идёт о тензорном анализе на (римановом или псевдоримановом, с которыми обычно имеют дело в классическом подходе, по крайней мере, на первом этапе) многообразии общего вида, все эти операции определяются обычно общековариантным способом (то есть способом, не зависящим от выбора криволинейных координат) с помощью метрического тензора.

Основными тензорными операциями являются сложение, в этом подходе сводящееся к покомпонентному сложению, аналогично векторам, и свёртка — с векторами, между собой и сами с собой, обобщающая матричное умножение, скалярное произведение векторов и взятие следа матрицы. Умножение тензора на число (на скаляр) можно при желании считать частным случаем свёртки, оно сводится к покомпонентному умножению.

Значения чисел в массиве, или компоненты тензора, зависят от системы координат, но при этом сам тензор, как геометрическая сущность, от них не зависит. Под проявлениями этой геометрической сущности можно понимать много что: различные скалярные инварианты, симметричность/антисимметричность индексов, соотношения между тензорами и другое. Например, скалярное произведение и длина векторов не меняется при поворотах осей, а метрический тензор всегда остаётся симметричным. Свёртки любых тензоров с самими собой и/или другими тензорами (в том числе векторами), если в результате не осталось ни одного индекса, являются скалярами, то есть инвариантами относительно замены координат: это общий способ постороения скалярных инвариантов.

При замене системы координат компоненты тензора преобразуются по определённому линейному закону.

Зная компоненты тензора в одной координатной системе, всегда можно вычислить его компоненты в другой, если задана матрица преобразования координат. Таким образом, второй подход можно суммировать в виде формулы:

тензор = массив компонент + закон преобразования компонент при замене базиса

Следует заметить, что при этом подразумевается, что все тензоры (все тензоры над одним векторным пространством), независимо от их ранга (то есть и векторы в том числе), преобразуются через одну и ту же матрицу преобразования координат (и дуальную ей, если есть верхние и нижние индексы). Компоненты тензора, таким образом, преобразуется по тому же закону, что и соответствующие компоненты тензорного произведения векторов (в количестве, равном валентности тензора), учитывая ковариантность-контравариантность компонент.

Например, компоненты тензора

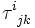
$\tau^i_{\ jk}$

преобразуется так же, как компоненты тензорного произведения трёх векторов, то есть как произведение компонент этих векторов

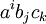
$\ a^ib_jc_k$

Так как преобразование компонент вектора известно, то таким образом можно легко сформулировать простейший из вариантов классического определения тензора.

Примеры

Тензор ранга (0,0) — это скаляр;
Один раз контравариантный тензор (ранга (0,1)) — это просто элемент пространства V, то есть вектор;
Тензор ранга (1,0) есть ковектор (ковариантный вектор), то есть элемент пространства V * (или линейный функционал на V, 1-форма);
Тензор ранга (2,0) есть билинейная форма, например метрический тензор g i j на касательном пространстве.
Тензор ранга (1,1) есть линейный оператор или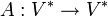
- В частности, единичный оператор, который может быть представлен единичной матрицей $\delta^i_j$ — тензор ранга (1,1).
Форма объёма на _n_-мерном линейном пространстве есть пример антисимметрического тензора ранга (0,n) (или n раз ковариантного)
Риманова кривизна в естественном виде 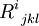$R^i_{\ jkl}$ — пример тензора ранга (3,1), её свёртки — тензор Риччи R i j и скалярная кривизна R = R i j g i j — примеры тензоров соответственно ранга (2,0) и (0,0) — то есть последний — скаляр.

Как следует из определения, компоненты тензора должны меняться определённым образом синхронно с компонентами векторов того пространства, на котором он определён, при преобразовании координат. Поэтому не любая табличка или величина с индексами, выглядящая как представление тензора, на самом деле представляет тензор.

Простым, хотя в целом несколько искусственным, примером такой таблички, не представляющей тензор, может быть табличка, компоненты которой представляют набор произвольных чисел, никак не меняющихся при произвольных преобразованиях координат. Такой объект не представляет тензора, или, во всяком случае, не представляет тензора на линейном пространстве, в котором произошло преобразование координат. Так, набор из трёх чисел не представляет трёхмерного вектора, если эти числа не преобразуются при замене координат совершенно определённым образом.
Также в общем случае подмножество компонент тензора высшего ранга не является тензором низшего ранга.
Не представляет тензора также объект, все компоненты которого нули хотя бы в одной невырожденной системе координат (в полном базисе), тогда как в другой хотя бы одна компонента ненулевая. Этот факт — следствие (поли-)линейности тензоров.

Существуют объекты, которые не только похожи на тензоры, но для которых определены (и имеют разумный и корректный смысл) тензорные операции (свёртка с другими тензорами, в частности, с векторами), однако при этом тензорами не являющиеся:

Прежде всего к тензорам не относятся сами матрицы (матрицы Якоби) преобразования координат, являющегося частным случаем диффеоморфизма между двумя многообразиями, с помощью которых и вводится классическое определение тензора, хотя по многим своим свойствам они напоминают тензор. Для них также можно ввести верхние и нижние индексы, операции умножения, сложения и свёртки. Однако, в отличие от тензора, компоненты которого зависят лишь от координат на заданном многообразии, компоненты матрицы Якоби также зависят от координат на многообразии-образе. Это различие очевидно в том случае, когда рассматриваются матрицы Якоби диффеоморфизма двух произвольных многообразий, однако при отображении многообразия в себя его можно не заметить, так как касательные пространства образа и прообраза изоморфны (не канонически). Тем не менее, оно сохраняется. Аналогию между матрицами Якоби и тензорами можно развить, если рассматривать произвольные векторные расслоения над многообразием и их произведения, а не только касательное и кокасательное расслоение.
Символы Кристоффеля 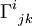$\Gamma^i_{\ jk}$ также не представляют тензора, хотя бы потому, что они могут быть обращены в ноль выбором координат вблизи произвольной точки, так же, как выбором (криволинейных) координат могут быть сделаны ненулевыми. Однако свёртка компонент связности с вектором дает настоящий вектор, а их разность — настоящий тензор (тензор кручения). Символы Кристоффеля, как и любые коэффициенты связности на расслоении, являются элементами более сложного пространства, чем пространство тензоров — расслоения струй.

Тензорные операции

Тензоры допускают следующие алгебраические операции:

Умножение на скаляр — как и вектор или скаляр (частные случаи тензора);
Сложение тензоров одинаковой валентности и состава индексов (вычислять сумму можно покомпонентно, как и для векторов);
- Наличие умножения на скаляр и сложения тензоров делают пространство тензоров одного и того же типа линейным пространством.
Свёртка тензора — специфическая тензорная операция, понижающая валентность тензора, вычисляется суммированием по паре индексов (верхнего и нижнего, если они различаются) и пробегающих, оставаясь равными друг другу, все свои значения, например:
- (последнее в эйнштейновских обозначениях, где суммирование по повторяющемуся верхнему и нижнему индексу подразумевается автоматически). Часто, если не как правило, свёртка (то есть результат операции свёртки) обозначается той же буквой, что и тензор, к которому свёртка применена, только, конечно, с количеством индексов, на два меньшим.
След матрицы — частный случай свёртки тензора с собой.
Свёртка двух или нескольких тензоров (в том числе тензоров и векторов), например:
(последнее — в записи Эйнштейна).
— операция, которую можно свести к последовательному тензорному умножению этих тензоров (см. чуть ниже) и затем свёртке получившегося тензора (возможно, несколько раз). Очевидно, эта операция линейна по всем входным каналам. Таким образом, свёртка с тензором реализует линейное или полилинейное отображение пространств тензоров на пространство тензоров (в общем случае — на другое), в частности, векторов на векторы и векторов на скаляры.
- Свёртка вектора с тензором валентности два есть действие линейного оператора, определяемого этим тензором, на вектор:
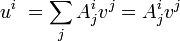  $u^i\ = \sum_j A^i_j v^j = A^i_j v^j$ (последнее — в записи Эйнштейна).
- Свёртка (однократная) двух тензоров валентности два реализует композицию линейных операторов, определяемых этими тензорами:
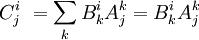  $C^i_j\ = \sum_k B^i_k A^k_j = B^i_k A^k_j$ (последнее — в записи Эйнштейна).

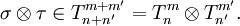
$\sigma\otimes\tau\in T^{m+m'}_{n+n'}=T^{m}_n\otimes T^{m'}_{n'}.$

Компоненты тензорного произведения суть произведения соответствующих компонент множителей, например:

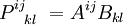
$P^{ij}_{\ \ kl}\ = A^{ij} B_{kl}$

Симметрии

В различного рода приложениях часто возникают тензоры с определённым свойством симметрии.

Симметричным по двум ко-(контра-)вариантным индексам называется тензор, который удовлетворяет следующему требованию:

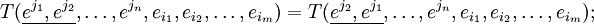
$T(\underline{e^{j_1},e^{j_2}},\ldots,e^{j_n},e_{i_1},e_{i_2},\ldots,e_{i_m}) = T(\underline{e^{j_2},e^{j_1}},\ldots,e^{j_n},e_{i_1},e_{i_2},\ldots,e_{i_m});$

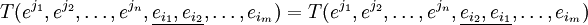
$T(e^{j_1},e^{j_2},\ldots,e^{j_n},\underline{e_{i_1},e_{i_2}},\ldots,e_{i_m}) = T(e^{j_1},e^{j_2},\ldots,e^{j_n},\underline{e_{i_2},e_{i_1}},\ldots,e_{i_m})$

или в компонентах

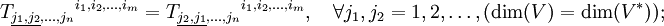
${T_{\underline{j_1,j_2},\ldots,j_n}}^{i_1,i_2,\ldots,i_m} = {T_{\underline{j_2,j_1},\ldots,j_n}}^{i_1,i_2,\ldots,i_m},\quad \forall j_1,j_2 = 1,2,\ldots,(\dim(V)=\dim(V^*));$

${T_{j_1,j_2,\ldots,j_n}}^{\underline{i_1,i_2},\ldots,i_m} = {T_{j_1,j_2,\ldots,j_n}}^{\underline{i_2,i_1},\ldots,i_m},\quad \forall i_1,i_2 = 1,2,\ldots,(\dim(V)=\dim(V^*)).$

Аналогично определяется косая симметрия (или антисимметричность):

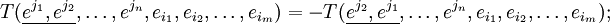
$T(\underline{e^{j_1},e^{j_2}},\ldots,e^{j_n},e_{i_1},e_{i_2},\ldots,e_{i_m}) = -T(\underline{e^{j_2},e^{j_1}},\ldots,e^{j_n},e_{i_1},e_{i_2},\ldots,e_{i_m});$

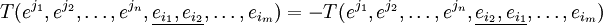
$T(e^{j_1},e^{j_2},\ldots,e^{j_n},\underline{e_{i_1},e_{i_2}},\ldots,e_{i_m}) = -T(e^{j_1},e^{j_2},\ldots,e^{j_n},\underline{e_{i_2},e_{i_1}},\ldots,e_{i_m})$

или в компонентах

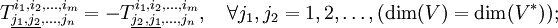
$T_{\underline{j_1,j_2},\ldots,j_n}^{i_1,i_2,\ldots,i_m} = -T_{\underline{j_2,j_1},\ldots,j_n}^{i_1,i_2,\ldots,i_m},\quad \forall j_1, j_2 = 1,2,\ldots,(\dim(V)=\dim(V^*));$

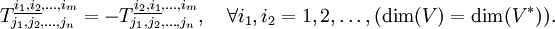
$T_{j_1,j_2,\ldots,j_n}^{\underline{i_1,i_2},\ldots,i_m} = -T_{j_1,j_2,\ldots,j_n}^{\underline{i_2,i_1},\ldots,i_m},\quad \forall i_1, i_2 = 1,2,\ldots,(\dim(V)=\dim(V^*)).$

Симметрия или антисимметрия не обязательно должна охватывать только соседние индексы, она может включать в себя любые индексы, учитывая, правда, следующее: симметрия или антисимметрия может относиться только к индексам одного сорта: ко- или контравариантным. Симметрии же, смешивающие ко- и контравариантные индексы тензоров, как правило, не имеют особого смысла, так как, даже если они наблюдаются в компонентах, то разрушаются при переходе к другому базису отнесения (то есть неинвариантны).

Впрочем, в присутствии метрического тензора, наличие операций поднятия или опускания индекса устраняет это неудобство, и ограничение этим по сути снимается, когда тензор представлен подходящим образом (так, например, тензор кривизны Римана 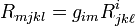$R_{mjkl}=g_{im}R^i_{jk\ell}$ антисимметричен по первым двум и последним двум индексам).

Эти определения естественным образом обобщаются на случай более чем двух индексов. При этом при любой перестановке индексов, по которым тензор является симметричным, его действие не изменяется, а при антисимметрии по индексам знак действия тензора изменяется на противоположный для нечётных перестановок (получаемых из начального расположения индексов нечётным числом транспозиций — перестановок двух индексов) и сохраняется для чётных.

Существуют и более сложные симметрии, например первое тождество Бьянки для тензора кривизны.

Тензоры в физике

В физике тензоры широко используются в теориях, обладающих геометрической природой (таких, как Общая теория относительности (ОТО)) или допускающих полную или значительную геометризацию (к каковым можно в значительной степени отнести практически все современные фундаментальные теории, поскольку они являются лоренц-ковариантными и допускают четырехмерную запись с использованием пространства Минковского, в частности, электродинамика, релятивистская механика и т. д.), а также в теории анизотропных сред (которые могут быть анизотропны изначально, как кристаллы низкой симметрии, или вследствие своего движения или напряжений, как текущая жидкость или газ, или как деформированное твердое тело). Кроме того, тензоры широко используются в механике абсолютно твердого тела.

Линейные операторы квантовой механики, конечно, также могут быть интерпретированы как тензоры над некими абстрактными пространствами (пространствами состояний), но традиционно такое применение термина тензор практически не используется, как и вообще крайне редко используется для описания линейных операторов над бесконечномерными пространствами. Вообще в физике термин тензор имеет тенденцию применяться только к тензорам над обычным физическим 3-мерным пространством или 4-мерным пространством-временем, или, в крайнем случае, над наиболее простыми и прямыми обобщениями этих пространств, хотя принципиальная возможность применения его в более общих случаях не является секретом.

Примерами тензоров в физике являются:

метрический тензор над псевдоримановым 4-мерным многообразием, являющийся в ОТО развитием понятия ньютоновского гравитационного потенциала.
выражающийся через него тензор Римановой кривизны и его свёртки, связанные в этой же теории с энергией гравитационного поля и непосредственно входящие в основное уравнение теории.
тензор электромагнитного поля над пространством Минковского, содержащий напряженности электрического и магнитного поля и являющийся главным объектом классической электродинамики в 4-мерной записи. В частности, уравнения Максвелла записываются с его помощью в виде единственного 4-мерного уравнения.
напряжения и деформации в теории упругости описываются тензорами над 3-мерным евклидовым пространством. То же касается таких величин, как модули упругости.
едва ли не большинство величин, являющихся скалярными характеристиками вещества в случае изотропности последнего, являются тензорами в случае анизотропного вещества. Говоря конкретнее, это относится к субстанциальным коэффициентам, связывающим векторные величины или стоящие перед произведениями (в частности, квадратами) векторов. Примерами могут быть удельная электропроводность (также и обратное ей удельное сопротивление), теплопроводность, диэлектрическая восприимчивость и диэлектрическая проницаемость, скорость звука (зависящая от направления) и т. д.
в механике абсолютно твердого тела важнейшую роль играет тензор инерции, связывающий угловую скорость с моментом импульса и кинетической энергией вращения. Этот тензор отличается от большинства других тензоров в физике, представляющих собой, вообще говоря, тензорные поля, тем, что один тензор характеризует одно абсолютно твердое тело, полностью определяя, вместе с массой, его инерцию.
аналогичным свойством обладают тензоры, входящие в мультипольное разложение: всего один тензор целиком представляет момент распределения зарядов соответствующего порядка в данное время.
часто в физике полезен псевдотензор Леви-Чивиты, входящий, например, в координатную запись векторного и смешанного произведений векторов. Компоненты этого тензора всегда записываются практически одинаково (с точностью до скалярного множителя, зависящего от метрики), а в правом ортонормированном базисе — совершенно одинаково всегда (каждая равна 0, +1 или −1).

Нетрудно заметить, что большинство тензоров в физике (не рассматривая скаляров и векторов) имеют всего два индекса. Тензоры, имеющие большую валентность (такие, как тензор Римана в ОТО) встречаются, как правило, только в теориях, считающихся достаточно сложными, да и то нередко фигурируют в основном в виде своих свёрток меньшей валентности. Большинство симметрично или антисимметрично.

Простейшей иллюстрацией, позволяющей понять физический (и отчасти геометрический) смысл тензоров, а более точно — симметричных тензоров второго ранга, будет, вероятно, рассмотрение тензора (удельной) электропроводности σ. Интуитивно понятно, что анизотропная среда, например, кристалл, или даже какой-то специально изготовленный искусственный материал, не будет в общем случае проводить ток одинаково легко во всех направлениях (например, из-за формы и ориентации молекул, атомных слоев или каких-то надмолекулярных структур — можно представить себе, например, тонкие проволочки хорошо проводящего металла, одинаково ориентированные и вплавленные в плохо проводящую среду). Возьмем за основу для простоты и конкретности, последнюю модель (хорошо проводящие проволочки в плохо проводящей среде). Электропроводность вдоль проволочек будет большой, назовем ее σ1, а поперек — маленькой, обозначим ее σ2. (Ясно, что в общем случае (например, когда проволочки сплюснуты в сечении и эта сплюснутость также ориентирована у всех проволочек одинаково, электропроводность σ3 будет отличаться от σ2, в случае же круглых равномерно распределенных проволочек — σ2 = σ3, но не равны σ1). Довольно нетривиальный в общем случае, но довольно очевидный в нашем примере, факт состоит в том, что найдутся три взаимно перпендикулярных направления, для которых связь вектора плотности тока $\mathbf{j}$ и напряженности вызывающего его электрического поля $\mathbf{E}$ будут связаны просто числовым множителем (в нащем примере — это направление вдоль проволочек, второе — вдоль их сплюснутости и третье перепендикулярное первым двум). Но любой вектор можно разложить на компоненты по этим удобным направлениям:

$\mathbf{E} = E_1 \mathbf{e}_1 + E_2 \mathbf{e}_2 + E_3 \mathbf{e}_3$

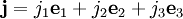
$\mathbf{j} = j_1 \mathbf{e}_1 + j_2 \mathbf{e}_2 + j_3 \mathbf{e}_3$

тогда можно для каждой компоненты записать:

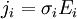
$\ j_i = \sigma_i E_i$

И мы увидим, что для любого направления, не совпадающего с 1, 2 и 3, вектор 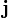$\mathbf{j}$ уже не будет совпадать по направлению с 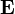$\mathbf{E}$ , если только не равны хотя бы два из σ1, σ2 и σ3.

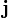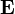Переходя к произвольным декартовым координатам, не совпадающим с этими выделенными направлениями, мы вынуждены будем включить матрицу поворота для преобразования координат, и поэтому в произвольной системе координат соотношение между $\mathbf{j}$ и $\mathbf{E}$ будет выглядеть так:

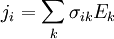
$\ j_i = \sum_k \sigma_{ik} E_k$

то есть тензор электропроводности будет представлен симметричной матрицей 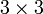$3 \times 3$ .

Учитывая же то, что удельная мощность тепловыделения w в проводнике равна скалярному произведению 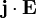$\mathbf{j}\cdot\mathbf{E}$ , нетрудно записать:

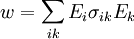
$\ w = \sum_{ik} E_i \sigma_{ik} E_k$

или

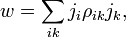
$\ w = \sum_{ik} j_i \rho_{ik} j_k,$

где ρ — удельное сопротивление — матрица, обратная матрице σ. Так мы наглядно видим еще одно типичное использование симметричного тензора второго ранга в физике — как квадратичной формы, преобразующей вектор в скаляр.

В этом примере для простоты использовались только прямоугольные равномасштабные декартовы координаты, поэтому различие верхних и нижних тензорных индексов отсутствует.

Таким образом, мы получили (правда, говоря строго, только для случая симметричного тензора) хороший наглядный геометрический образ тензора, применимый в физике. Этот образ состоит из ортогонального базиса (называемого собственным базисом тензора или его собственными координатами), ориентированного в пространстве определенным образом (определяемым свойствами среды, порождающей тензор), и трех (для трехмерного пространства) чисел (коэффициентов), связанных каждое с одной из этих осей (называемых собственными числами или собственными значениями тензора), предназначенных для умножения на них соответствующих компонент вектора, чтобы получить компоненты вектора нового. Как видим, в частном случае σ1 = σ2 = σ3 умножение на тензор σ сводится к умножению на число (на скаляр).

Или, умножая квадраты этих компонент (компонент в собственном базисе тензора) вектора на собственные числа, и сложив их, получаем скаляр. Поверхности уровня такой квадратичной формы — эллипсоиды. Такой эллипсоид служит также хорошим геометрическим образом тензора. Направление его главных осей — дает собственный базис тензора, а их величины — определяют его собственные числа.

В алгебре же всё сказанное иллюстрирует понятия собственных векторов (собственного базиса) и собственных чисел линейного оператора, квадратичной формы или матрицы, а процесс нахождения собственного базиса и собственных чисел (называемый задачей на собственные значения) называется диагонализацией оператора, квадратичной (или билинейной) формы или матрицы (так как матрица, представляющая оператор или билинейную форму становится в этом базисе диагональной).

Литература

Акивис М. А., Гольдберг В. В. Тензорное исчисление. — М.: Наука, 1969;
Кочин Н. Е. Векторное исчисление и начала тензорного исчисления (9-е издание). — М.: Наука, 1965;
Мак-Коннел А. Дж. Введение в тензорный анализ с приложениями к геометрии, механике и физике. — М.: Физматлит, 1963;
Номидзу К. Группы Ли и дифференциальная геометрия. — М.: ИЛ, 1960;
Победря Б. Е. Лекции по тензорному анализу: Учеб. пособие. (3-е изд.). — М.: Изд-во МГУ, 1986;
Рашевский П. К. Риманова геометрия и тензорный анализ (3-е издание). — М.: Наука, 1967;
Шарипов Р. А. Быстрое введение в тензорный анализ. — БашГУ.

См. также

Wikimedia Foundation.2010.