Исчисление | это... Что такое Исчисление? (original) (raw)

Исчисле́ние (лат. calculus — небольшой камешек, используемый для подсчёта) является разделом математики, изучающем пределы, функции, производные, интегралы и бесконечные ряды. Этот раздел представляет собой основную часть современного математического образования. Он состоит из двух основных частей: дифференциального исчисления и интегрального исчисления, которые связаны между собой основной теоремой исчисления. Исчисление является изучением изменений,[1] также как геометрия изучает формы, а алгебра изучает математические операции и их применение к решению уравнений. Изучение исчислений является ключом к другим, более продвинутым разделам математики, посвящённым изучению функций и пределов, которые в широком смысле называются математическим анализом. Исчисление имеет широкое применение в науке, экономике и технике, и может решить многие проблемы, для которых методов алгебры недостаточно.

Исторически сложилось так, что исчисление называется «исчислением бесконечно малых величин». В более общем смысле к исчислению относится любой метод или система расчёта, руководствующаяся символической манипуляцией выражениями. Примерами других известных исчислений являются исчисление высказываний, вариационное исчисление, лямбда-исчисление, пи-исчисление и соединённое исчисление.

Содержание

История

Античность

В античный период появились некоторые идеи, которые в дальнейшем привели к интегральному исчислению, но в ту эпоху эти идеи не были развиты строгим, систематическим образом. Расчёты объёмов и площадей, являющиеся одной из целей интегрального исчисления, можно найти в московском математическом папирусе из Египта (ок. 1820 до н.э.), но формулы являются скорее инструкциями, без каких-либо указаний на метод, а некоторые просто ошибочны.[2] В эпоху греческой математики Евдокс (ок. 408-355 до н.э.) для вычисления площадей и объемов использовал метод исчерпывания, который предвосхищает понятие предела, а позже эту идею дальше развил Архимед (ок. 287-212 до н.э.), изобретя эвристики, которые напоминают методы интегрального исчисления.[3] Метод исчерпывания позже изобрёл в Китае Лю Хуэй в III веке нашей эры, который он использовал для вычисления площади круга.[4] В V нашей эры Цзу Чунчжи разработал метод вычисления объёма шара, который позже назовут принципом Кавальери.[5]

Средневековье

В XIV веке индийский математик Мадхава Сангамаграма и астрономо-математическая школа Керала ввели многие компоненты исчисление, такие как ряды Тейлора, аппроксимацию бесконечных рядов, интегральный признак сходимости, ранние формы дифференциирования, почленное интегрирование, итерационные методы для решения нелинейных уравнений и определение того, что площадь под кривой является её интегралом. Некоторые считают, что «Юктибхаза» (Yuktibhāṣā) является первым трудом по математическому анализу.[6]

Современная эпоха

"Исчисление было первым достижением современной математики, и трудно переоценить его значение. Я думаю, что оно, больше, чем что-либо ещё, однозначно определяет отправную точку современной математики, а математический анализ, который является его логическим развитием, по-прежнему определяет наибольший технический прогресс в точном мышлении ". — Джон фон Нейман[7]

В Европе основополагающим трудом стал трактат Бонавентура Кавальери, в котором он утверждал, что объёмы и площади могут быть рассчитаны как суммы объёмов и площадей бесконечно тонкого сечения. Идеи были похожи на то, что изложил Архимед в работе «Метод», но этот трактат Архимеда был утерян до первой половины XX века. Работа Кавальери не была признана, так как его методы могли привести к ошибочным результатам, и бесконечно малым величинам он создал сомнительную репутацию.

Формальное исследование исчисления бесконечно малых, которое Кавальери соединил с исчислением конечных разностей, проводилось в Европе примерно в это же время. Пьер Ферма, утверждая, что он заимствовал это из Диофанта, ввёл понятие «квази-равенства» (англ. adequality), которое представляло собой равенство с точностью до бесконечно малой ошибки.[8] Большой вклад внесл также Джон Валлис, Исаак Барроу и Джеймс Грегори. Последние два около 1675 года доказали вторую фундаментальную теорему исчисления.

Исааком Ньютоном были введены правило произведения и правило цепочки, понятие производных высших порядков, ряды Тейлора и аналитические функции в своеобразных обозначениях, которые он использовал при решении задач математической физики. В своих публикациях Ньютон перефразировал свои идеи в соответствии с математическим языком того времени, заменяя вычисления бесконечно малых посредством других равнозначных форм геометрических представлений, которые считались безупречными. Он использовал методы исчисления для решения проблем движения планет, форм поверхностей вращающейся жидкости, сплюснутости Земли, скольжении груза по циклоиде и многих других проблем, которые он изложил в своём труде Математические начала натуральной философии (1687). В другой работе он разработал разложение функций в ряд, в том числе с использование дробных и иррациональных степеней, и было ясно, что он понял принципы рядов Тейлора. Не все свои открытия он публиковал, поскольку в то время методы бесконечно малых имели сомнительную репутацию.

Эти идеи были систематизированы в истинное исчисление бесконечно малых Готфридом Вильгельмом Лейбницем, который первоначально был обвинён Ньютоном в плагиате.[9] В настоящее время он рассматривается как независимый изобретатель и разработчик исчисления. Его вклад заключается в разработке чётких правил для работы с бесконечно малыми величинами, позволящих вычисление производных второго и более высоких порядков, а также в разработке правила произведения и правила цепочки в их дифференциальной и интегральной формах. В отличие от Ньютона, Лейбниц уделял большое внимание формализму, часто затрачивая многие дни для выбора подходящих символов для конкретных понятий.

Изобретение исчисления обычно приписывают обоим, и Лейбницу и Ньютону. Ньютон первым применил исчисление к общей физике, а Лейбниц разработал большую часть обозначений, используемых в исчислении сегодня. Основная проницательность, которую проявили как Ньютон, так и Лейбниц, заключалась в открытии законов дифференцирования и интегрирования, введении производных второго и более высоких порядков и введении понятия аппроксимации полиномов рядами. Во времена Ньютона основная теорема исчисления была уже известна.

Когда Ньютон и Лейбниц впервые опубликовали свои результаты, в то время не было серьёзных разногласий по поводу приоритета математика (а, следовательно, и страны) на это новшество. Ньютон получил свои результаты первым, но Лейбниц первым опубликовал свои. Позже Ньютон стал утверждать, что Лейбниц украл его идеи из неопубликованных заметок, которыми Ньютон поделился с несколькими членами Королевского общества. Эта полемика отделяла англоговорящих математиков от своих континентальных коллег на протяжении многих лет, в ущерб английской математике. Тщательное изучение работ Лейбница и Ньютона показало, что они получили свои результаты независимо друг от друга, Лейбниц начинал с интегрирования, а Ньютон с дифференцирования. Сегодня разработка исчисления засчитывается как Ньютону, так и Лейбницу. Название новой дисциплины мы получили от Лейбница. Ньютон называл своё исчисление «методы производных».

Со времён Лейбница и Ньютона многие математики внесли свой вклад в дальнейшее развитие исчисления. Одной из первых наиболее полных работ по анализу конечных и бесконечно малых была книга, написанная в 1748 году Марией Гаэтаной Аньези.[10]

Основания

В математике основания относятся к строгому определению предмета, отталкиваясь от точных аксиом и определений. На начальном этапе развития исчисления использование бесконечно малых величин считалось нестрогим, оно подвергалось жёсткой критике рядом авторов, в первую очередь Мишелем Роллем и епископом Беркли. Беркли превосходно описал бесконечно малые как «призраки умерших количеств» в своей книге «The Analyst» в 1734 году. Разработка строгих основ для исчисления заняло математиков на протяжении более столетия после Ньютона и Лейбница, и до сих пор сегодня в некоторой степени является активной областью исследований.

Несколько математиков, в том числе Маклорен, пытались доказать обоснованность использования бесконечно малых, но это удалось сделать только 150 лет спустя трудами Коши и Вейерштрасса, которые наконец-то нашли средства, как уклониться от простых «мелочёвок» бесконечно малых величин, и были положены начала дифференциального и интегрального исчисления. В трудах Коши мы находим универсальный спектр основополагающих подходов, в том числе определение непрерывности в терминах бесконечно малых и (несколько неточный) прототип (ε, δ)-определения предела в определении дифференцирования. В своём труде Вейерштрасс формализует понятие предела и устраняет бесконечно малые величины. После этого труда Вейерштрасса общей основой исчисления стали пределы, а не бесконечно малые величины. Бернхард Риман использовал эти идеи, чтобы дать точное определение интеграла. Кроме того, в этот период идеи исчисления были обобщены на евклидово пространство и на комплексную плоскость.

В современной математики основы исчисления включаются в раздел вещественного анализа, который содержит полные определения и доказательства теорем исчисления. Сфера исследований исчисления стала значительно шире. Анри Лебег разработал теорию мер множества и использовал её для определения интегралов от всех функций, кроме самых экзотических. Лоран Шварц ввёл в рассмотрение обобщённые функции, которые можно использовать для вычисления производных любой функции вообще.

Введение пределов определило не единственный строгий подход к основанию исчисления. Альтернативой может быть, например, нестандартный анализ Абрахама Робинсона. Подход Робинсона, разработанный в 1960-е годы, использует технические средства из математической логики для расширения системы вещественных чисел бесконечно малыми и бесконечно большими числами, как это было в исходной концепции Ньютона-Лейбница. Эти числа, называемые гипердействительными, можно использовать в обычных правилах исчисления, подобно тому, как это делал Лейбниц.

Важность

Хотя некоторые идеи исчисления ранее были разработаны в Египте, Греции, Китае, Индии, Ираке, Персии и Японии, современное использование исчисления началось в Европе в XVII веке, когда Исаак Ньютон и Готфрид Вильгельм Лейбниц построили на базе работ предшествующих математиков его основные принципы. Развитие исчислении был основано на более ранних концепциях мгновенного движения и площади под кривой.

Дифференциальное исчисление применяется в расчётах, связанных со скоростью и ускорением, углом наклона кривой и оптимизацией. Применение интегрального исчисления включает расчёты с участием площадей, объёмов, длин дуг, центров масс, работы и давления. Более сложные приложения включают расчёты степенных рядов и рядов Фурье.

Исчисление также используется для получения более точного представления о природе пространства, времени и движения. Веками математики и философы боролись с парадоксами, связанными с делением на ноль или нахождением суммы бесконечного ряда чисел. Эти вопросы возникают при изучении движения и вычислении площадей. Древнегреческий философ Зенон Элейский дал несколько известных примеров таких парадоксов. Исчисление предоставляет инструменты для разрешения этих парадоксов, в частности, пределы и бесконечные ряды.

Принципы

Пределы и бесконечно малые величины

Исчисление обычно имеет дело с манипулированием очень малыми количествами. Исторически первыми такими объектами были бесконечно малые величины. Их можно рассматривать как числа, но всё-таки они «бесконечно малые». Бесконечно малое число dx больше 0, но меньше, чем любое из чисел в последовательности 1, 1/2, 1/3, ... и меньше, чем любое положительное вещественное число. Взятая кратное число раз, бесконечно малая по-прежнему остаётся бесконечно малой, то есть бесконечно малые не удовлетворяют аксиоме Архимеда. С этой точки зрения исчисление представляет собой набор методов для работы с бесконечно малыми. Такой подход не стал поддерживаться в XIX веке, потому что трудно было представить понятие бесконечно малой точным. Тем не менее, концепция была возрождена в XX веке с появлением нестандартного анализа и гладкого анализа бесконечно малых, который обеспечил прочную основу для манипуляции бесконечно малыми.

В XIX веке бесконечно малыми были заменены пределами. Пределы описывают значение функции для некоторого входа с точки зрения его значения для соседнем входа. Они охватывают мелкомасштабные изменения, подобно как бесконечно малым, но используются для обычной системы вещественных чисел. В этой трактовке исчисление представляет собой набор методов для манипуляции некоторыми пределами. Бесконечно малые заменяются на очень небольшие числа, а бесконечно малые изменения функции находятся путём принятия предельного поведения при всё меньших и меньших числах. Пределы являются самым лёгким способом создать строгую основу для исчисления, и по этой причине они приняты в качестве стандартного подхода.

Дифференциальное исчисление

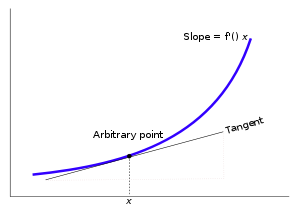
Касательная в точке (x, f(x)). Производная f′(x) кривой в точке равна наклону касательной к этой кривой в данной точке.

Дифференциальное исчисление изучает определение, свойства и применение производных функций. Процесс нахождения производной называется дифференцированием. Для заданной функции и точки из области её определения производная в этой точке является способом кодирования мелкомасштабного поведение этой функции вблизи этой точки. Найдя производную функции в каждой точке в области определения, можно определить новую функцию, называемую производной функцией или просто производной от исходной функции. На математическом языке производная является линейным отображением, на входе которого одна функция, а на выходе другая. Это понятие является более абстрактным, чем большинство процессов, изучаемых в элементарной алгебре, где функции обычно имеют на входе одно число, а на выходе другое. Например, если функции удвоения задать на входе три, на выходе будет шесть; если для квадратичной функции задать на входе три, на выходе будет девять. Производная же может иметь квадратичную функцию в качестве входа. Это означает, что производная берёт всю информацию о функции возведения в квадрат, то есть: при входе два, она даёт на выходе четыре, три преобразует в девять, четыре — в шестнадцать и так далее, и использует эту информацию для получения другой функции. (Производной квадратичной функции является как раз функция удвоения.)

Наиболее распространенным символом для обозначения производной является апострофо-подобный знак, называемый штрихом. Таким образом, производная функции f есть f′, произносится «f штих». Например, если f(x) = x_2 является функцией возведения в квадрат, то f′(x) = 2_x является её производной, это функция удвоения.

Если входом функции является время, то производная представляет собой изменение по времени. Например, если f является функцией, зависящей от времени, и она даёт на выходе положение мяча во времени, то производная f определяет изменение положение мяча по времени, то есть скорость мяча.

Если функция является линейной (то есть, если графиком функции является прямая линия), то функцию можно записать в виде y = mx + b, где x — независимая переменная, y — зависимая переменная, а b — это _y_-отсечка, при этом:

m= \frac{\text{rise}}{\text{run}}= \frac{\text{change in } y}{\text{change in } x} = \frac{\Delta y}{\Delta x}.

Это выражение даёт точное значение угла наклона прямой линии. Если график функции не является прямой линией, то изменение y делённое на изменение x меняется от точки к точке. Производная даёт точный смысл понятия изменения выходного значения по отношению к изменению входа. Чтобы быть конкретным, пусть f есть функция, и мы фиксируем точку a в области определения f. (a, f(a)) является точкой на графике функции. Если h — близкое к нулю число, то a + h является числом, близким к a. Поэтому точка (a + h, f(a + h)) близка к точке (a, f(a)). Угол наклона между этими двумя точками равен:

m = \frac{f(a+h) - f(a)}{(a+h) - a} = \frac{f(a+h) - f(a)}{h}.

Это выражение называется разностным соотношением. Линия, проходящая через две точки на кривой, называется секущей линией, поэтому m является углом наклона секущей линии между (a, f(a)) и (a + h, f(a + h)). Секущая является лишь приближением к поведению функции в точке, поскольку она не учитывает поведение функции между точками a и (a + h, f(a + h)). Определить это поведении, установив a равным нулю, невозможно, поскольку потребовалось бы делить на ноль, что исключено. Производная определяется путём перехода к пределу при h стремящемся к нулю, что означает, что он рассматривает поведение f для всех малых значениях h и выделяет приемлемое значение для случая, когда h равно нулю:

\lim_{h \to 0}{f(a+h) - f(a)\over{h}}.

Геометрически производная равна углу наклона касательной к графику функции f в точке a. Касательная является пределом секущих линий, так же как производная является пределом разностных соотношений. По этой причине производную иногда называют наклоном функции f.

Вот конкретный пример, производная функция возведения в квадрат в точке 3. Пусть f(x) = _x_2 является квадратичной функцией.

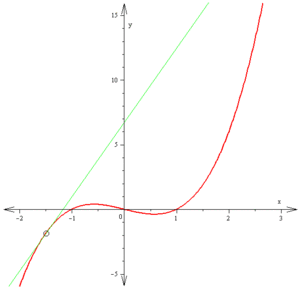
Производная f′(x) кривой в точке есть наклон касательной к этой кривой в данной точке. Этот наклон определяется путём нахождения предельной величины наклона секущих. Здесь используется функция f(x) = _x_3 − x (изображена красным цветом). Касательная (зелёный цвет), которая проходит через точку (-3/2, −15/8), имеет наклон 23/4. Обратите внимание, что вертикальный и горизонтальный масштаб в этом изображении разные.

\begin{align}f'(3) &=\lim_{h \to 0}{(3+h)^2 - 3^2\over{h}} \\ &=\lim_{h \to 0}{9 + 6h + h^2 - 9\over{h}} \\ &=\lim_{h \to 0}{6h + h^2\over{h}} \\ &=\lim_{h \to 0} (6 + h) \\ &= 6. \end{align}

Наклон касательной к квадратичной функции в точке (3,9) равно 6, то есть она растёт вверх в шесть раз быстрее, чем отклоняется право. Вычисление предела, описанное выше, можно выполнить для любой точки в области определения квадратичной функции. Это определяет производную функцию или просто для краткости производную от функции возведения в квадрат. Проведённые расчёты показывают что производная квадратичной функции есть функция удвоения.

Нотация Лейбница

Введённые Лейбницем обозначения для производной в приведённом выше примере выглядят так:

\begin{align} y&=x^2 \\ \frac{dy}{dx}&=2x. \end{align}

В подходе, основанном на пределах, символ dy/dx следует интерпретировать не как частное от деления двух чисел, а как сокращённое обозначение для вычисленного выше предела. Лейбниц не стремился представить его как отношение двух бесконечно малых чисел: dy — бесконечно малого изменения y, и dx — бесконечно малого изменения x, вызвавшее изменение y. Можно считать, что d/dx является оператором дифференцирования, который берёт одну функцию на входе и выдаёт на выходе другую функцию — производную. Например:

\frac{d}{dx}(x^2)=2x.

При таком понимании dx в знаменателе читается «относительно х». Даже при представлении исчисления с использованием пределов, а не бесконечно малых, обозначение является общим для манипулирования символами, как если бы dx и dy были реальными числами. Хотя, чтобы избежать подобных манипуляций, такие обозначения иногда удобно использовать в выражении операции, как, например, это применяется при обозначении полной производной.

Интегральное исчисление

Интегральное исчисление — это изучение определения, свойств и применения двух взаимосвязанных понятий: неопределённого интеграла и определённого интеграла. Процесс поиска значения интеграла называется интегрированием. В технических терминах интегральное исчисление является исследованием двух связанных линейных операторов.

Неопределённый интеграл является первообразной, то есть операцией, обратной к производной. F является неопределённым интегралом от f в том случае, когда f является производной от F. (Это использование прописных и строчных букв для функции и её неопределённого интеграла распространено в исчислении).

Определенный интеграл входной функции и выходных значений есть число, которое равно площади поверхности, ограниченной графиком функции, осью абсцисс и двумя отрезками прямых линий от графика функции до оси абсцисс в точках выходных значений. В технических терминах определённый интеграл есть предел суммы площадей прямоугольников, называемой суммой Римана.

Примером из физики является вычисление пройденного расстояния при ходьбе в любой момент времени.

\mathrm{Distance} = \mathrm{Speed} \cdot \mathrm{Time}

Если скорость постоянна, достаточно операции умножение, но если скорости меняется, то мы должны применить более мощный метод вычисления расстояния. Одним из таких методов является приблизительное вычисление путём разбивки времени на отдельные короткие промежутки. Умножая затем время в каждом интервале на какую-либо одну из скоростей в этом интервале и затем суммируя все приблизительные расстояния (сумма Римана), пройденные в каждом интервале, мы получим полное пройденное расстояние. Основная идея состоит в том, что если использовать очень короткие интервалы, то скорость на каждом из них будет оставаться более или менее постоянной. Тем не менее, сумма Римана даёт только приблизительное расстояние. Чтобы найти точное расстояние, мы должны найти предел всех таких сумм Римана.

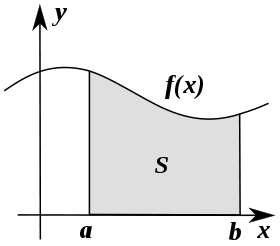
Интегрирование можно рассматривать как вычисление площади под кривой, определённой уравнением f(x), между двумя точками (здесь a и b).

Если f(x) на диаграмме слева представляет изменение скорости с течением времени, то пройденное расстояние (между моментами a и b) есть площадь заштрихованной области s.

Для приближённой оценки этой площади возможен интуитивный метод, состоящий в разделении расстояния между a и b на некоторое число равных отрезков (сегментов) длиной Δx. Для каждого сегмента мы можем выбрать одно значение функции f(x). Назовём это значение h. Тогда площадь прямоугольника с основанием Δx и высотой h даёт расстояние (время Δx умноженной на скорость h), пройденное в этом сегменте. С каждым сегментом связывается среднее значение функции на нём _f(x)_=h. Сумма всех таких прямоугольников даёт приближение площади под кривой, которая является оценкой общего пройденного расстояния. Уменьшение Δx даст большее количество прямоугольников и в большинстве случаев будет лучшим приближением, но для получения точного ответа мы должны вычислить предел при Δx стремящемся к нулю.

Символом интегрирования является \int \,, удлиненная буква S (S означает «сумма»). Определённый интеграл записывается в виде:

\int_a^b f(x)\, dx.

и читается: «интеграл от a до b функции f от x по _x_». Предложенное Лейбницем обозначения dx предназначено для разделения площади под кривой на бесконечное число прямоугольников, таких, что их ширина Δx является бесконечно малой величиной dx. В формулировке исчисления, основанного на пределах, обозначение

\int_a^b \ldots\, dx

должно пониматься как оператор, который принимает на входе функцию и даёт на выходе число, равное площади. dx не является числом и не умножается на f(x).

Неопределённый интеграл, или первообразная, записывается в виде:

\int f(x)\, dx.

Функции, отличающиеся на константу, имеют те же производные, и, следовательно, первообразная данной функции на самом деле является семейством функций, отличающиеся только константой. Поскольку производная функции y = x_² + C, где C — любая константа, равна y′ = 2_x, то первообразная последней определяется по формуле:

\int 2x\, dx = x^2 + C.

Неопределённая константа типа C в первообразной известна как постоянная интегрирования.

Основная теорема

Основная теорема исчисления утверждает, что дифференцирование и интегрирование являются взаимно обратными операциями. Точнее, это касается значения первообразных для определённых интегралов. Поскольку, как правило, легче вычислить первообразную, чем применять формулу определённого интеграла, основная теорема исчисление даёт практический способ вычисления определённых интегралов. Она также может быть интерпретирована как точное утверждение о том, что дифференцирование является обратной операцией интегрирования.

Фундаментальная теорема исчисления гласит: если функция f непрерывна на отрезке [a, _b_] и если F есть функция, производная которой равна f на интервале (a, b), то:

\int_{a}^{b} f(x)\,dx = F(b) - F(a).

Кроме того, для любого x из интервала (a, b)

\frac{d}{dx}\int_a^x f(t)\, dt = f(x).

Это понимание, сделанное как Ньютоном, так и Лейбницем, которые основывали свои результаты на более ранних трудах Исаака Барроу, было ключом к быстрому распространению аналитических результатов после того, как их работы стали известны. Фундаментальная теорема даёт алгебраический метод вычисления многих определённых интегралов без ограничения процессов, путём нахождения формулы первообразной. Кроме того, возник прототип для решения дифференциальных уравнений. Дифференциальные уравнения связывают неизвестные функции с их производными, они применяются повсеместно во многих науках.

Применение

Исчисление используется во многих отраслях физических наук, в актуарных расчётах, информатике, статистике, технике, экономике, бизнесе, медицине, демографии и других областях, в которых для решения проблемы может быть построена математическая модель, и желательно найти её оптимальное решение. Исчисление позволяет перейти от некоторого распределения скоростей изменения к полному изменению и наоборот, очень часто при решении проблем мы знаем что-нибудь одно и пытаемся найти другое.

Методы теоретической физики служат прекрасной иллюстрацией применения исчислений, все понятия в классической механике и электромагнетизме связаны между собой именно через исчисление. Например, при известном распределении плотности объекта его масса, моменты инерции, а также полная энергия в потенциальном поле могут быть найдены с помощью исчисления. Хорошим примером использования исчисления в механике может служить второй закон Ньютона: исторически сложилось так, что в нём напрямую используется термин «скорость изменения», который относится к производной, говоря: скорость изменения импульса тела равна результирующей силе, действующей на тело в том же направлении. Обычная формулировка сегодня: Сила = масса × ускорение, включает в себя дифференциальное исчисление, поскольку ускорение есть производная по времени от скорости или вторая производная по времени от траектории или пространственного положения. Зная, как объект ускоряется, мы используем исчисление для вычисления его пути.

Теория электромагнетизма Максвелла и общая теория относительности Эйнштейна также выражаются языком дифференциального исчисления. В химии исчисление используется при определении скорости реакций и скорости радиоактивного распада. В биологии с помощью исчисления делается расчёт динамики популяций, учитывающей данные по воспроизводству и смертности вида.

Исчисление может использоваться в сочетании с другими математическими дисциплинами. Например, оно может использоваться совместно с линейной алгеброй, чтобы найти «наилучшую» линейную аппроксимацию для множества точек в области определения. Или его можно использовать в теории вероятностей для определения вероятности непрерывной случайной величины в зависимости от плотности распределения. В аналитической геометрии при изучении графиков функций исчисление используется для поиска точек максимума и минимума, наклона, кривизны и точек перегиба.

Теорема Грина, которая устанавливает соотношение между криволинейным интегралом по простой замкнутой кривой С и двойным интегралом по плоской области D, ограниченной этой кривой С, применяется в инструменте, известном как планиметр, который используется для расчёта площади плоской поверхности на чертеже. Например, его можно использовать для расчёта площади фигуры неправильной формы: цветника или бассейна при проектировании своего участка.

Дискретная теорема Грина, устанавливающая соотношение между двойным интегралом функции по периметру прямоугольника C и линейной комбинацией значений первообразной по угловым точкам прямоугольника, позволяет быстро вычислить сумму площадей прямоугольных областей. Например, она может использоваться для эффективного расчета суммы прямоугольных областей на изображениях, для того чтобы быстро находить свойства и идентифицировать объекты.

В области медицины исчисление можно применить для нахождения оптимального угла ветвления кровеносных сосудов, максимизирующего поток. Зная закон затухания применительно к выводу какого-либо препарата из тела, исчисление используется для оценки уровня дозирования этих препаратов. В ядерной медицине исчисление используется для разработки моделей переноса излучения в целевой терапии опухолей.

В экономике исчисление позволяет определить максимальную прибыль, предоставляя способ легкого вычисления как предельных издержек, так и предельного дохода.

Исчисление используется также для нахождения приближённых решений уравнений. На практике это стандартный способ решения дифференциальных уравнений и нахождение корней в большинстве приложений. Примерами являются метод Ньютона, метод простой итерации и метод линейной аппроксимации. Например, при расчётах траектории космических аппаратов используется вариант метода Эйлера для аппроксимации криволинейных курсов движения при отсутствии силы тяжести.

См. также

Примечания

  1. ↑ Latorre, Donald R.; Kenelly, John W.; Reed, Iris B. & Biggers, Sherry (2007), «Calculus Concepts: An Applied Approach to the Mathematics of Change», Cengage Learning, с. 2, ISBN 0-618-78981-2, <http://books.google.com/books?id=bQhX-3k0LS8C> , Chapter 1, p 2
  2. ↑ Morris Kline, Mathematical thought from ancient to modern times, Vol. I
  3. ↑ Archimedes, Method, in The Works of Archimedes ISBN 978-0-521-66160-7
  4. ↑ (1966) «A comparison of Archimdes' and Liu Hui's studies of circles» (Springer) 130., Chapter , p. 279
  5. ↑ Calculus: Early Transcendentals. — 3. — Jones & Bartlett Learning, 2009. — P. xxvii. — ISBN 0-763-75995-3, Extract of page 27
  6. ↑ Indian mathematics
  7. ↑ von Neumann, J., «The Mathematician», in Heywood, R. B., ed., The Works of the Mind, University of Chicago Press, 1947, pp. 180—196. Reprinted in Bródy, F., Vámos, T., eds., The Neumann Compedium, World Scientific Publishing Co. Pte. Ltd., 1995, ISBN 9810222017, pp. 618—626.
  8. ↑ André Weil: Number theory. An approach through history. From Hammurapi to Legendre. Birkhauser Boston, Inc., Boston, MA, 1984, ISBN 0817645659, p. 28.
  9. ↑ Leibniz, Gottfried Wilhelm. The Early Mathematical Manuscripts of Leibniz. Cosimo, Inc., 2008. Page 228. Copy
  10. ↑ Unlu, Elif Maria Gaetana Agnesi. Agnes Scott College (April 1995). Архивировано из первоисточника 5 сентября 2012.

Ссылки