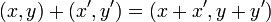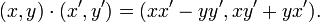Мнимые числа | это... Что такое Мнимые числа? (original) (raw)

Запрос «Комплексные числа» перенаправляется сюда. Cм. также другие значения.

Ко́мпле́ксные[1][2] чи́сла — расширение множества вещественных чисел, обычно обозначается 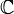$\mathbb{C}$ . Любое комплексное число может быть представлено как формальная сумма x + i y, где x и y — вещественные числа, i — мнимая единица, то есть число, удовлетворяющее уравнению _i_2 = − 1. (В физике символ i часто заменяют на j, чтобы не путать с стандартным обозначением электрического тока (i)).

Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени n с комплексными коэффициентами имеет ровно n комплексных корней, то есть верна основная теорема алгебры. Это одна из основных причин широкого применения комплексных чисел в математических исследованиях. Кроме того, применение комплексных чисел позволяет удобно и компактно сформулировать многие математические модели, применяемые в математической физике и в естественных науках — электротехнике, гидродинамике, картографии, квантовой механике, теории колебаний и многих других.

Содержание

1 Определения
2 Действия над комплексными числами
3 Связанные определения
- 3.1 Сопряжённые числа
4 Представление комплексных чисел
5 История
6 Функции комплексного переменного
7 См. также
8 Примечания
9 Ссылки

Определения

Поле комплексных чисел можно понимать как расширение поля вещественных чисел, в котором многочлен _z_2 + 1 имеет корень. Следующие две элементарные модели показывают, что непротиворечивое построение такой системы чисел возможно. Оба приведенных определения приводят к изоморфным расширениям поля вещественных чисел 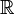$\R$ , как и любые другие конструкции поля разложения многочлена _x_2 + 1.

Стандартная модель

Формально, комплексное число z — это упорядоченная пара вещественных чисел (x,y) с введёнными на них следующим образом операциями сложения и умножения:

$(x , y) + (x' , y') = (x + x' , y + y') \,$
$(x , y) \cdot (x' , y') = (xx' - yy' , xy' + yx'). \,$

Вещественные числа представлены в этой модели парами вида (x,0), причём операции с такими парами согласованы с обычными сложением и умножением вещественных чисел. Мнимая единица в такой системе представляется парой 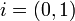$i=(0,1) \,$ .

Несложно показать, что определённые выше операции имеют те же свойства, что и аналогичные операции с вещественными числами. Исключением являются только свойства, связанные с отношением порядка (больше-меньше), потому что расширить порядок вещественных чисел, включив в него все комплексные числа и при этом сохранив обычные свойства порядка, невозможно.

Матричная модель

Комплексные числа можно также определить как семейство вещественных матриц вида

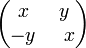
$\begin{pmatrix} x & y \\ -y & \;\; x \end{pmatrix}$

с обычным матричным сложением и умножением. Действительной единице будет соответствовать

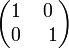
$\begin{pmatrix} 1 & 0 \\ 0 & \;\; 1 \end{pmatrix}$

, мнимой единице —

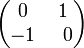
$\begin{pmatrix} 0 & 1 \\ -1 & \;\; 0 \end{pmatrix}$

Замечания

Ошибочно определение числа i как единственного числа, удовлетворяющего уравнению _x_2 = − 1, так как число ( − i) также удовлетворяет этому уравнению.
Следует также заметить, что часто используемое выражение 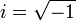$i=\sqrt{-1}$ не вполне корректно, так как алгебраический корень определяется над множеством неотрицательных чисел.

Действия над комплексными числами

Сравнение
a + b i = c + d i означает, что a = c и b = d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
Сложение
(a + b i) + (c + d i) = (a + c) + (b + d)i
Вычитание
(a + b i) − (c + d i) = (a − c) + (b − d)i
Умножение
(a + b i)(c + d i) = a c + b c i + a d i + b d _i_2 = (a c − b d) + (b c + a d)i
Деление
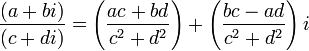
$\,\frac{(a + bi)}{(c + di)} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc - ad \over c^2 + d^2} \right)i\,$

Связанные определения

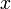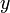Пусть и — вещественные числа такие, что комплексное число 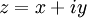~z=x+iy (обычные обозначения). Тогда

Сопряжённые числа

Если комплексное число z = x + i y, то число 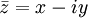$\bar z=x-iy$ называется сопряжённым (или комплексно сопряжённым) к z.

Переход к сопряжённому числу можно рассматривать как одноместную операцию; перечислим её свойства.

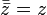$\bar \bar z = z$ (сопряжённое к сопряжённому есть исходное)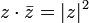
$z \cdot \bar z = |z|^2$
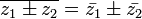
$\overline {z_1 \pm z_2} = \bar {z_1} \pm \bar {z_2}$
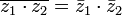
$\overline {z_1 \cdot z_2} = \bar z_1 \cdot \bar z_2$
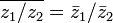
$\overline {z_1 / z_2} = \bar z_1 / \bar z_2$

Обобщение: 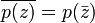$\overline {p(z)} = p(\bar z)$ , где p(z) — произвольный комплексный многочлен.

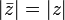$|\bar{z}| = |z|$ (модуль сопряжённого числа такой же, как у исходного)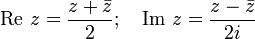
$\operatorname{Re}\ z=\frac {z+\bar z}{2}; \quad \operatorname{Im}\ z=\frac {z-\bar z}{2i}$

Представление комплексных чисел

Алгебраическая форма

Запись комплексного числа 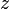в виде 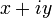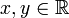~x + iy , $~x,y\in\R$ , называется алгебраической формой комплексного числа.

Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что 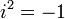~i^2 = -1 ):

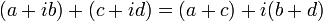
~(a + ib) + (c + id) = (a+c) + i(b+d)

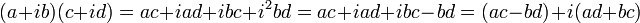
~(a + ib) (c + id) = ac + iad + ibc + i^2bd = ac + iad + ibc - bd = (ac-bd) + i(ad+bc)

Тригонометрическая и показательная формы

Если вещественную x и мнимую y части комплексного числа выразить через модуль 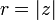~r=|z| и аргумент 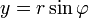$\varphi$ ( $x=r\cos\varphi$ , $y=r\sin\varphi$ ), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме

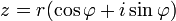$z=r(\cos\varphi+i \sin\varphi)$ .

Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера

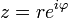$z=re^{i\varphi}$ ,

где 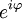$e^{i\varphi}$ — расширение экспоненты для случая комплексного показателя степени.

Отсюда вытекают следующие широко используемые равенства:

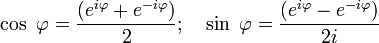
$\cos\ \varphi=\frac{(e^{i\varphi}+e^{-i\varphi})}{2}; \quad \sin\ \varphi=\frac{(e^{i\varphi}-e^{-i\varphi})}{2i}$

Геометрическое представление

Геометрическое представление комплексного числа

Модуль, аргумент, вещественная и мнимая части

Если на плоскости по оси абсцисс расположить действительную часть, а по оси ординат — мнимую, то комплексному числу будет соответствовать точка с декартовыми координатами x и y (или её радиус-вектор, что то же самое), а модуль и аргумент будут полярными координатами этой точки. Такая плоскость называется комплексной.

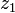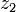Отметим, что для пары комплексных чисел $z_1\,$ и $z_2\,$ модуль их разности: 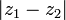$|z_1-z_2|\,$ равен расстоянию между соответствующими точками комплексной плоскости.

Геометрическое представление сопряжённых чисел

Сопряжённые комплексные числа получаются зеркальным отражением друг друга относительно вещественной оси.

В геометрическом представлении сумма комплексных чисел соответствует векторной сумме соответствующих векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Если модуль второго сомножителя равен 1, то умножение на него геометрически означает поворот радиус-вектора первого числа на угол, равный аргументу второго числа. Этот факт объясняет широкое использование комплексного представления в теории колебаний.

Формула Муавра

Корни пятой степени из единицы (вершины пятиугольника)

Эта формула позволяет возводить в степень ненулевое комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид:

$z^n=[r(\cos \varphi +i\sin \varphi)]^n = r^n(\cos n\varphi +i\sin n\varphi)$ ,

где r — модуль, а $\varphi$ — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 году.

Аналогичная формула применима также и при вычислении корней _n_-ой степени из ненулевого комплексного числа:

$z^{1/n}=[r(\cos (\varphi+2\pi k) +i\sin (\varphi+2\pi k))]^{1/n} =$
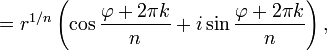
$= r^{1/n}\left(\cos \frac{\varphi+2\pi k}{n} +i\sin \frac{\varphi+2\pi k}{n}\right),$
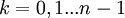
$\quad k=0,1...n-1$

Отметим, что корни _n_-й степени из комплексного числа всегда существуют, и их количество равно n. На комплексной плоскости, как видно из формулы, все эти корни являются вершинами правильного _n_-угольника, вписанного в окружность радиуса $\sqrt[n]{r}$ с центром в начале координат (см. рисунок).

История

Впервые, по-видимому, мнимые величины появились в известном труде «Великое искусство, или об алгебраических правилах» Кардано (1545), который счёл их непригодными к употреблению. Пользу мнимых величин, в частности, при решении кубического уравнения, в так называемом неприводимом случае (когда вещественные корни многочлена выражаются через кубические корни из мнимых величин), впервые оценил Бомбелли (1572). Он же дал некоторые простейшие правила действий с комплексными числами.

Выражения вида 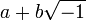$a+b\sqrt{-1}$ , появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в XVI-XVII веках, однако даже для многих крупных ученых XVII века алгебраическая и геометрическая сущность мнимых величин представлялась неясной. Лейбниц, например, писал: «Дух божий нашел тончайшую отдушину в этом чуде анализа, уроде из мира идей, двойственной сущности, находящейся между бытием и небытием, которую мы называем мнимым корнем из отрицательной единицы».[3]

Долгое время было неясно, все ли операции над комплексными числами приводят к комплексным результатам, или, например, извлечение корня может привести к открытию какого-то нового типа чисел. Задача о выражении корней степени n из данного числа была решена в работах Муавра (1707) и Котса (1722).

Символ 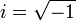$i=\sqrt{-1}$ предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву слова imaginarius. Он же распространил все стандартные функции, включая логарифм, на комплексную область. Эйлер также высказал в 1751 году мысль об алгебраической замкнутости поля комплексных чисел. К такому же выводу пришел Д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит Гауссу (1799). Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 году, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году.

Геометрическое истолкование комплексных чисел и действий над ними появилось впервые в работе Весселя (1799). Первые шаги в этом направлении были сделаны Валлисом (Англия) в 1685 году. Современное геометрическое представление, иногда называемое «диаграммой Аргана», вошло в обиход после опубликования в 1806-м и 1814-м годах работы (Аргана (фр.)), повторявшей независимо выводы Весселя.

Арифметическая модель комплексных чисел как пар вещественных чисел была построена Гамильтоном (1837); это доказало непротиворечивость их свойств. Гамильтон предложил и обобщение комплексных чисел — кватернионы, алгебра которых некоммутативна.

Функции комплексного переменного

См. также

Кватернионы
Гиперкомплексные числа — конечномерные алгебры над полем вещественных чисел.
Комплексная функция
Комплексный анализ

Примечания

↑ Школьная энциклопедия «Математика». Издательство «Большая Российская энциклопедия». 1996 год. Гл. ред. С.М. Никольский.
↑ «Русский орфографический словарь» Российской академии наук под ред. В. В. Лопатина указывает ударение компле́ксный, ряд других словарей допускают оба варианта ударения, см. ГРАМОТА.РУ
↑ Клайн М. Математика. Утрата определённости. — М.: Мир, 1984. — С. 139.

Ссылки

Арнольд В. И. Геометрия комплексных чисел, кватернионов и спинов, МЦНМО, 2002
Елисеев В. И. «Введение в методы теории функций пространственного комплексного переменного», Центр научно-технического творчества молодежи Алгоритм. — М.:, НИАТ. — 1990. Шифр Д7-90/83308
Понтрягин Л. Комплексные числа, Квант, № 3, 1982.
Простой калькулятор комплексных чисел
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 2001. — Т. II. — 680 с. — ISBN 5-9221-0156-0, 5-9221-0155-2, 5-9221-0436-5
CaRevol Jet — Формульный калькулятор комплексных чисел под Windows.

Wikimedia Foundation.2010.