Плоская кривая | это... Что такое Плоская кривая? (original) (raw)
Кривая или линия — геометрическое понятие, определяемое в разных разделах геометрии различно.
Содержание
- 1 Элементарная геометрия
- 2 Параметрические определения
- 3 Кривая Жордана
- 4 Аналитические определения
- 5 Типы кривых
- 6 Обобщённые кривые
- 7 См. также
- 8 Литература
- 9 Ссылки
Элементарная геометрия
В рамках элементарной геометрии понятие кривой не получает отчётливой формулировки и иногда определяется как «длина без ширины» или как «граница фигуры». По существу в элементарной геометрии изучение кривых сводится к рассмотрению примеров (прямая, отрезок, ломаная, окружность и др.). Не располагая общими методами, элементарная геометрия довольно глубоко проникла в изучение свойств конкретных кривых (конические сечения, некоторые алгебраические кривые высших порядков и также трансцендентные кривые), применяя в каждом случае специальные приёмы.
Параметрические определения
Чаще всего кривая определяется как непрерывное отображение из отрезка в пространство:
![\gamma:[a,b]\to X](https://dic.academic.ru/pictures/wiki/files/97/a198424df9949df08c8e4c125b74c5b6.png)
При этом, кривые могут быть различными, даже если их образы совпадают. Такие кривые называют параметризованными кривыми или, если [a,_b_] = [0,1], путями.
Иногда кривая определяется с точностью до репараметризации, то есть с точностью до минимального отношения эквивалентности такого что параметрические кривые
![\gamma_1:[a_1,b_1]\to X](https://dic.academic.ru/pictures/wiki/files/101/e4dc362b365ed1ad1d17fd79b0ecefef.png) и
и ![\gamma_2:[a_2,b_2]\to X](https://dic.academic.ru/pictures/wiki/files/53/58e1660ea9664b329c447836f7f780b1.png)
эквивалентны, если существует непрерывная монотонная функция (иногда неубывающая) h из отрезка [_a_1,_b_1] на отрезок [_a_2,_b_2], такая что
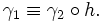
Определяемые этим отношением классы эквивалентности называются непараметризованными кривыми или просто кривыми.
Кривая Жордана
Кривой Жордана называется образ непрерывного инъективного отображения окружности или отрезка в пространство. В случае окружности кривая называется замкнутой кривой Жордана, а в случае отрезка — жордановой дугой или простой дугой.
Следует отметить что кривая Жордана является довольно сложным объектом, например возможно построить плоскую кривую Жордана с ненулевой мерой Лебега.
Комментарий
Существует большой соблазн определить кривую как образ непрерывного отображения отрезка в пространство.
Однако возможно построить такое непрерывное отображение отрезка в плоскость, что его образ заполняет квадрат, например, кривая Пеано. Более того, согласно теореме Мазуркевича, компактное связанное и локально связанное топологическое пространство является непрерывным образом отрезка. Таким образом, не только квадрат, но и куб любого числа измерений и даже гильбертов кирпич являются непрерывными образами отрезка.
Вышеизложенное показывает, что кривая не может быть определена как непрерывный образ отрезка, если на отображение не наложить дополнительных ограничений.
Аналитические определения
В аналитической геометрии кривая на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению F(x,y) = 0. При этом на функцию F накладываются ограничения, которые гарантируют, что
- это уравнение имеет бесконечное множество несовпадающих решений и,
- это множество решений не заполняло «куска плоскости».
Алгебраические кривые
Важный класс кривых составляют те, для которых функция F(x,y) есть многочлен от двух переменных. В этом случае кривая, определяемая уравнением F(x,y) = 0, называется алгебраической.
- Алгебраические кривые, задаваемые уравнением 1-й степени, суть прямые.
- Уравнение 2-й степени, имеющее бесконечное множество решений, определяет квадрики, то есть вырожденные и не вырожденные конические сечения.
- Примеры кривых, задаваемых уравнениями 3-ей степени: циссоида Диокла, Декартов лист.
- Примеры кривых 4-ой степени: лемниската Бернулли и овал Кассини.
- Пример кривой, определяемой уравнением чётной степени: (многофокусная) лемниската.
Алгебраические кривые, определяемые уравнениями высших степеней, рассматриваются в алгебраической геометрии. При этом бо́льшую стройность приобретает их теория, если рассмотрение ведется на комплексной проективной плоскости. В этом случае алгебраическая кривая определяется уравнением вида
F(_z_1,_z_2,_z_3) = 0,
где F — однородный многочлен трех переменных, являющихся проективными координатами точек.
Типы кривых
- Плоская кривая — кривая, все точки которой лежат в одной плоскости.
- Простая дуга
- Путь — непрерывное отображение отрезка [0,1] в топологическое пространство.
- Трансцендентная кривая
Типы точек на кривой
Обобщённые кривые
Более общее определение кривой для случая плоскости было дано Кантором в 1870-e годы:
Канторовой кривой называется компактное связное подмножество плоскости, такое что его дополнение всюду плотно.
Важный пример канторовой кривой доставляет ковёр Серпинского. Какова бы ни была канторова кривая L, она может быть вложена в ковёр Серпинского, то есть в ковре Серпинского содержится подмножество L', гомеоморфное L. Таким образом ковёр Серпинского является универсальной плоской канторовой кривой.
В последствии это определение было обобщено Урысоном:
Кривой Урысона называется связное компактное топологическое пространство C топологической размерности 1.
Ковёр Серпинского удовлетворяет этому определению, так что всякая канторова кривая является также и кривой Урысона. Обратно, если плоский связный компакт является кривой Урысона, то он будет канторовой кривой.
См. также
Литература
- Бураго Д. Ю., Бураго Ю. Д., Иванов С. В. Курс метрической геометрии НИЦ РХД, Институт компьютерных исследований, Инст-т компьют. исслед., Ин-т комп.исслед., ИКИ, , ISBN 5-93972-300-4, 2004
- Математический энциклопедический словарь. М. «Советская энциклопедия», 1988 г.
Ссылки
Wikimedia Foundation.2010.