Лемниската Бернулли | это... Что такое Лемниската Бернулли? (original) (raw)

Лемниската и её фокусы
Лемниска́та Берну́лли — плоская алгебраическая кривая. Определяется как геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами.
Лемниската по форме напоминает восьмёрку или символ бесконечности.
Содержание
История
Название происходит от греч. λημνισχος — лента, повязка. В Древней Греции «лемнискатой» называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх. Эту лемнискату называют в честь швейцарского математика Якоба Бернулли, положившего начало её изучению.
Уравнение лемнискаты впервые опубликовано в статье Curvatura Laminae Elasticae Якоба Бернулли в журнале Acta eruditorum в 1694 году. Бернулли назвал эту кривую lemniscus и он не знал, что четырнадцатью годами ранее Джованни Кассини уже исследовал более общий случай[1]. Квадратуру лемнискаты впервые выполнил Джюлио-Карло Фаньяно (англ.), опубликовав в 1718 году статью Metodo per misurare la lemniscata и положив тем самым начало изучению эллиптических интегралов, продолженное впоследствии Леонардом Эйлером[2]. Некоторые свойства кривой были также исследованы Якобом Штейнером в 1835 году.
Уравнения
Рассмотрим простейший случай: если расстояние между фокусами  , расположены они на оси
, расположены они на оси  , и начало координат делит отрезок между ними пополам, то следующие уравнения задают лемнискату:
, и начало координат делит отрезок между ними пополам, то следующие уравнения задают лемнискату:

Вывод
Фокусы лемнискаты —  и
и  . Возьмём произвольную точку
. Возьмём произвольную точку  . Произведение расстояний от фокусов до точки
. Произведение расстояний от фокусов до точки  есть
есть
 ,
,
и по определению оно равно  :
:

Возводим в квадрат обе части равенства:

Раскрываем скобки в левой части:

Раскрываем скобки и свёртываем новый квадрат суммы:

Выносим общий множитель и переносим:

Далее можно сделать замену  , хотя это не обязательно:
, хотя это не обязательно:

В данном случае  — радиус окружности, описывающей лемнискату.
— радиус окружности, описывающей лемнискату.
Проведя несложные преобразования, можно получить явное уравнение:

Вывод

Возводим в квадрат и раскрываем скобки:

Приводим к виду

Это квадратное уравнение относительно  . Решив его, получим
. Решив его, получим

Взяв корень и отбросив вариант с отрицательным вторым слагаемым, получим:

где положительный вариант определяет верхнюю половину лемнискаты, отрицательный — нижнюю.


Плотность точек кривой при равномерном изменении параметра
- Параметрическое уравнение в прямоугольной системе:
 , где
, где 
Это единственный вариант рациональной параметризации кривой. Уравнение полностью описывает кривую, когда параметр пробегает всю вещественную прямую: от  до
до  . При этом, когда параметр стремится к
. При этом, когда параметр стремится к  , точка кривой стремится к
, точка кривой стремится к  из второй координатной четверти, а когда параметр стремится к
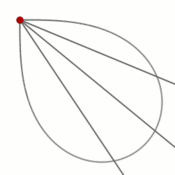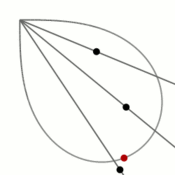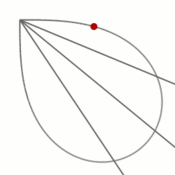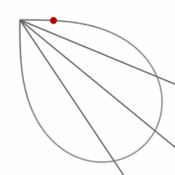
из второй координатной четверти, а когда параметр стремится к  , то — из четвёртой. Распределение точек, которые даёт параметрическое уравнение, при изменении его параметра с фиксированным шагом показано на рисунке.
, то — из четвёртой. Распределение точек, которые даёт параметрическое уравнение, при изменении его параметра с фиксированным шагом показано на рисунке.
Вывод уравнения
Уравнение лемнискаты в полярной системе

подставим в формулы перехода к полярной системе координат  возведённые в квадрат:
возведённые в квадрат:

Рассмотрим первое уравнение:

Используем тригонометрические формулы  и
и  :
:

Используем ещё одно легко выводимое тригонометрическое соотношение  :
:

После преобразований:

Извлекаем корень из обеих частей равенства:

Если произвести замену  , то получаем искомое выражение для
, то получаем искомое выражение для  :
:

Второе уравнение выводится аналогично с применением формулы  .
.
Чтобы задать лемнискату по двум произвольным точкам, можно не выводить уравнение заново, а определить преобразование координат, при котором старый (данный) фокусный отрезок переходит в новый, и воздействовать на представленные уравнения этим преобразованием.
Пример
Пусть, например,  — фокусы.
— фокусы.
Существует прямоугольная система координат (на рисунке —  ), в которой уравнение лемнискаты имеет вид
), в которой уравнение лемнискаты имеет вид

Необходимо определить преобразование системы координат, переводящее  в
в  . Это преобразование осуществляется в два этапа: параллельный перенос и поворот.
. Это преобразование осуществляется в два этапа: параллельный перенос и поворот.
Середина отрезка  —
—  , значит перенос только на
, значит перенос только на  по оси
по оси  :
:

После переноса системы координат её надо повернуть на некоторый угол. Для определения угла сначала найдём расстояние между фокусами:

значит  .
.
Теперь из геометрических соображений находим синус и косинус угла наклона  к
к  :
:


Формулы преобразования:

Совместив оба преобразования, получим конечные формулы перехода:

Для того, чтобы получить уравнение в стандартной системе координат, подставим эти соотношения в исходное уравнение кривой:

После преобразований:

Это уравнение задаёт лемнискату с фокусами  в стандартной прямоугольной системе координат.
в стандартной прямоугольной системе координат.
Свойства
Лемниската Бернулли является частным случаем овала Кассини при  , синусоидальной спирали с индексом
, синусоидальной спирали с индексом  и лемнискаты Бута при
и лемнискаты Бута при  , поэтому она наследует некоторые свойства этих кривых.
, поэтому она наследует некоторые свойства этих кривых.
Свойства от овала Кассини
Свойства от синусоидальной спирали
| Вывод |
|---|
Есть частный случай формулы радиуса кривизны синусоидальной спирали:  при при  однако, легко вывести и по определению. Уравнение лемнискаты в полярной системе: однако, легко вывести и по определению. Уравнение лемнискаты в полярной системе:  Формулы перехода к полярной системе координат: Формулы перехода к полярной системе координат:  Выражаем Выражаем  : :  Подставляем в уравнение лемнискаты и выражаем Подставляем в уравнение лемнискаты и выражаем  и и  : :  —- это параметрическое уравнение относительно —- это параметрическое уравнение относительно  . Проведя некоторые тригонометрические преобразования, можно получить уравнение относительно . Проведя некоторые тригонометрические преобразования, можно получить уравнение относительно  , указанное выше в разделе Уравнения. Формула радиуса кривизны кривой, заданной параметрически: 
Гравитационное свойство лемнискаты
Построения
При помощи секущих (способ Маклорена)
Строится окружность радиуса  с центром в одном из фокусов. Из середины
с центром в одном из фокусов. Из середины  фокусного отрезка строится произвольная секущая
фокусного отрезка строится произвольная секущая  (
( и
и  — точки пересечения с окружностью), и на ней в обе стороны откладываются отрезки
— точки пересечения с окружностью), и на ней в обе стороны откладываются отрезки  и
и  , равные хорде
, равные хорде  . Точки
. Точки  ,
,  лежат на разных петлях лемнискаты.
лежат на разных петлях лемнискаты.
Шарнирные методы
Вариант первый
На плоскости выбираются две точки —  и
и  — будущие фокусы лемнискаты. Собирается специальная конструкция из трёх скреплённых в ряд на шарнирах отрезков, чтобы полученная линия могла свободно изгибаться в двух местах (точки сгиба —
— будущие фокусы лемнискаты. Собирается специальная конструкция из трёх скреплённых в ряд на шарнирах отрезков, чтобы полученная линия могла свободно изгибаться в двух местах (точки сгиба —  и
и  ). При этом необходимо соблюсти пропорции отрезков:
). При этом необходимо соблюсти пропорции отрезков:  . Края линии крепятся к фокусам. При непараллельном вращении отрезков вокруг фокусов середина центрального отрезка опишет лемнискату Бернулли.
. Края линии крепятся к фокусам. При непараллельном вращении отрезков вокруг фокусов середина центрального отрезка опишет лемнискату Бернулли.
Вариант второй
В этом варианте лемниската строится по фокусу и двойной точке —  и
и  соответственно. Собирается почти такая же шарнирная конструкция как и в предыдущем варианте, но прикреплённый к двойной точке отрезок
соответственно. Собирается почти такая же шарнирная конструкция как и в предыдущем варианте, но прикреплённый к двойной точке отрезок  соединяется не с концом центрального
соединяется не с концом центрального  , а с его серединой. Пропорции также другие:
, а с его серединой. Пропорции также другие:  .
.
См. также
- Лемниската — общий случай с несколькими фокусами
- Овал Кассини — обобщение на произведение расстояний до фокусов
- Синусоидальная спираль — обобщение по виду параметрического уравнения
- Лемниската Бута
- Плоская кривая
- Алгебраическая кривая
- Бесконечность
- Аттрактор Лоренца
Примечания
- ↑ Статья об Овалах Кассини на сайте о плоских кривых (англ.). Архивировано из первоисточника 22 августа 2011. Проверено 15 июня 2010.
- ↑ Bradley R. E., D'Antonio L. A., Sandifer C. E. Euler at 300: an appreciation. — P. 121-123.
Литература
- Математическая энциклопедия (в 5-и томах). — М.: Советская Энциклопедия, 1982.
- Маркушевич А. И. Замечательные кривые. — Популярные лекции по математике. — М.: Гостехиздат, 1952. — С. 23-25.
- Савелов А. А. Плоские кривые / Под. ред. А. П. Нордена. — М.: ФИЗМАТГИЗ, 1960. — С. 155-162.
- Lockwood E. H. A book of curves. — Cambridge: Cambridge university press, 1961. — P. 110-117.
Ссылки
- Статья на сайте Wolfram MathWorld (англ.). Проверено 15 июня 2010.
- Статья в Encyclopédie des Formes Mathématiques Remarquables (фр.). Архивировано из первоисточника 22 августа 2011. Проверено 15 июня 2010.
- Фаньяно и длина дуги лемнискаты (итал.). Архивировано из первоисточника 22 августа 2011. Проверено 15 июня 2010.