Квадратриса | это... Что такое Квадратриса? (original) (raw)

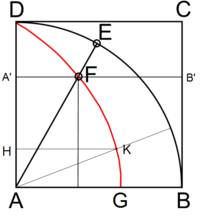
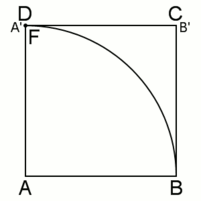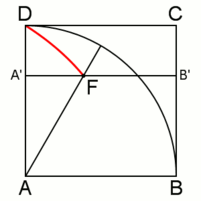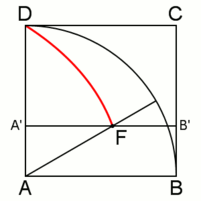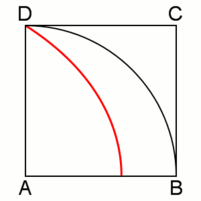
Рис. 1. Кинематическое определение квадратрисы

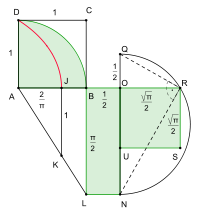
Рис. 2. То же с анимацией

Квадратриса — плоская трансцендентная кривая, определяемая кинематически. Была предложена в античные времена для решения задач квадратуры круга и трисекции угла.

Содержание

1 Кинематическое определение
2 История
3 Уравнения кривой
4 Основное свойство
5 Применение
- 5.1 Трисекция угла
- 5.2 Квадратура круга
6 Вариации
7 См. также
8 Примечания
9 Литература
10 Ссылки

Кинематическое определение

Рассмотрим квадрат ABCD (рис. 1), в который вписан сектор четверти круга. Пусть точка равномерно движется по дуге от точки до точки ; одновременно отрезок A'B' равномерно движется из положения в положение . Наконец, потребуем, чтобы оба движения начались и закончились одновременно. Тогда точка пересечения радиуса и отрезка A'B' опишет квадратрису (рис. 2, выделена красным цветом).

История

Первое упоминание о квадратрисе сделали Папп Александрийский [1] и Ямвлих в конце III века. Папп дал и подробное описание способов её построения. Кривая открыта, по сообщению Прокла Диадоха (V век), софистом Гиппием (V век до н. э.) и использовалась им для решения задачи трисекции угла. Другой античный геометр, Динострат, дал исследование этой кривой и показал, что она обеспечивает также решение задачи квадратуры круга. В источниках данную кривую называют «квадратрисой Динострата» или «квадратрисой Гиппия».

В Новое время кривую исследовали Роберваль (1636), Ферма, Барроу (1670) и другие известные математики. Декарт посвятил исследованию квадратрисы немало страниц в своей «Геометрии» (1637). Ньютон в 1676 году определил длину дуги квадратрисы, её кривизну и площадь её сегмента в виде ряда.

Уравнения кривой

В полярных координатах:

$\rho=\frac{2R}{\pi}\frac{\varphi}{\sin \varphi}.$

Вывод
Пусть — радиус круга, $\varphi$ — текущий угол , $\rho=AF$ — полярный радиус. Для удобства введём время , которое за период движения меняется от 0 до 1. Тогда равномерное движение точки по дуге длиной $\textstyle\frac{\pi}{2}$ можно выразить уравнением: $\varphi = \frac{\pi}{2}\cdot (1-t).$ Равномерное движение отрезка выражается уравнением: $A'A = \rho \sin \varphi = (1-t) R$ Подставляя значение из первого уравнения во второе, получаем окончательно: $\rho=\frac{2R\varphi}{\pi\sin \varphi}.$

Вывод

Пусть

— радиус круга, $\varphi$ — текущий угол FAG

, $\rho=AF$ — полярный радиус. Для удобства введём время

, которое за период движения меняется от 0 до 1. Тогда равномерное движение точки

по дуге длиной $\textstyle\frac{\pi}{2}$ можно выразить уравнением: $\varphi = \frac{\pi}{2}\cdot (1-t).$ Равномерное движение отрезка A'B'

выражается уравнением: $A'A = \rho \sin \varphi = (1-t) R$ Подставляя значение 1-t

из первого уравнения во второе, получаем окончательно: $\rho=\frac{2R\varphi}{\pi\sin \varphi}.$

В прямоугольных координатах:

$x=y\,\operatorname{ctg}\frac{\pi y}{2R}$

Вывод
Приводим уравнение в полярных координатах к виду: $\rho\sin\varphi=\frac{2R}{\pi}\varphi$ Учитывая $\rho\sin\varphi=y$ , получаем $y=\frac{2R}{\pi}\varphi$ Из геометрических соображений: $\textstyle\varphi=\operatorname{arctg}\frac{y}{x}$ . Тогда уравнение предстанет в виде: $\frac{\pi y}{2R}=\operatorname{arctg}\frac{y}{x}$ Берём тангенс от обеих частей: $\operatorname{tg}\frac{\pi y}{2R}=\frac{y}{x}$ то есть $x=y\,\operatorname{ctg}\frac{\pi y}{2R}$

Вывод

Приводим уравнение в полярных координатах к виду: $\rho\sin\varphi=\frac{2R}{\pi}\varphi$ Учитывая $\rho\sin\varphi=y$ , получаем $y=\frac{2R}{\pi}\varphi$ Из геометрических соображений: $\textstyle\varphi=\operatorname{arctg}\frac{y}{x}$ . Тогда уравнение предстанет в виде: $\frac{\pi y}{2R}=\operatorname{arctg}\frac{y}{x}$ Берём тангенс от обеих частей: $\operatorname{tg}\frac{\pi y}{2R}=\frac{y}{x}$ то есть $x=y\,\operatorname{ctg}\frac{\pi y}{2R}$

Основное свойство

Уравнение квадратрисы в полярных координатах можно записать в виде:

$\rho \sin \varphi = \frac{2R}{\pi} \varphi,$ или: $y = k \varphi,$

где $k =\frac{2R}{\pi}.$ Отсюда следует основное свойство данной кривой:

Ординаты любых двух точек квадратрисы относятся, как полярные углы этих точек: $\frac{y_1}{y_2} = \frac{\varphi_1}{\varphi_2}.$

Квадратриса — единственная (невырожденная) кривая в первом координатном квадранте, обладающая таким свойством (это легко доказать, повторив приведенные рассуждения в обратном порядке).

Применение

Трисекция угла

Трисекция угла, то есть деление произвольного угла на три равные части, с помощью квадратрисы проводится элементарно. Пусть EAB (рис. 1) — некоторый угол, треть которого надо построить. Алгоритм деления следующий:

Находим точку на квадратрисе и её ординату .
Откладываем на отрезке его третью часть; получим некоторую точку .
Находим на квадратрисе точку с ординатой .
Проводим луч . Угол — искомый.

Доказательство данного алгоритма сразу следует из основного свойства квадратрисы. Очевидно также, что аналогичным способом можно разделить угол не только на три, но и на любое другое число частей.

Квадратура круга

Рис. 3. Схема квадратуры круга с помощью квадратрисы

Задача квадратуры круга ставится так: построить квадрат с такой же площадью, как у заданного круга радиуса . Алгебраически это означает решение уравнения: $x^2=\pi R^2$ .

Построим для исходного круга квадратрису, как на рис. 1. Используя первый замечательный предел, получаем, что абсцисса её нижней точки равна $\frac {2R} {\pi}$ . Выразим это в виде пропорции: C:2R=2R:AG , где $C = 2 \pi R$ — длина окружности. Приведенное соотношение позволяет построить отрезок длины . Прямоугольник со сторонами и C/2 будет иметь нужную площадь, а построить равновеликий ему квадрат — дело несложное, см. статью Квадратура (математика) или рис. 3.

Вариации

Помимо рассмотренной выше квадратрисы Динострата, существует ряд иных кривых, которые можно использовать для квадратуры круга, и поэтому также называемых квадратрисами.

Квадратриса Чирнгауза (или Чирнгаузена):

$y=a \sin \frac{\pi x}{2a}$

Квадратриса Озанама:

$x=2 a \sin^2 \frac{y}{2a}$

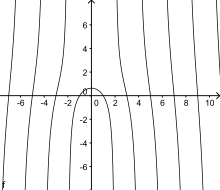
Рис. 4. График «полной» квадратрисы при R=1

Кроме того, ряд авторов предпочитают поменять местами x и y в уравнении квадратрисы Динострата:

$y=x\,\operatorname{ctg}\frac{\pi x}{2R}$

Этот вариант имеет то преимущество, что функция y(x) определена на всей вещественной оси, кроме точек $\pm 2 R, \pm 4 R, \pm 6 R \dots$ , см. её график при R=1 на рис. 4. В полярных координатах центральная ветка данного варианта кривой описывается формулой:

$\rho=\frac{R}{\pi} \cdot \frac{\pi-2 \varphi}{\cos \varphi}.$

См. также

Примечания

↑ Папп Александрийский. Математическое собрание, книга IV.

Литература

Жуков А. В.. «О числе π». М.: МЦНМО, 2002 г., 32 с ISBN 5-94057-030-5
Прасолов В. В.. Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга. М.: Наука, 1992. 80 с. Серия «Популярные лекции по математике», выпуск 62.
Прошлецова И. Л. О квадратрисе Динострата // Историко-математические исследования. СПб.: Изд-во Международного фонда истории науки. Вып. 35 (1994). С. 220—229.
Савелов А. А. Плоские кривые: Систематика, свойства, применения. М.: Физматгиз, 1960. 293 с. Переиздана в 2002 году, ISBN 5-93972-125-7.
Чистяков В. Д. Три знаменитые задачи древности. М.: Гос. уч.-пед. изд-во Министерства просвещения РСФСР, 1963.
Щетников А. И. Как были найдены некоторые решения трёх классических задач древности? Математическое образование, № 4 (48), 2008, с. 3-15.

Ссылки

Quadratrix of Hippias at the MacTutor archive. (англ.)
Quadratrix of Hippias at Convergence. (англ.)

Кривые
Определения	Аналитическая • Жордана • Канторова • Урысона • Овал • Спрямляемая Радиус кривизны
Преобразованные	Эволюта • Эвольвента • Подера • Антиподера • Параллельная • Дуальная • Каустика
Неплоские	Винтовая линия • Линия откоса • Локсодрома • Ортодромия • Губка
Плоские алгебраические
Конические сечения	Гипербола • Парабола • Эллипс (Окружность)
3-й порядок	Эллиптические: Эллиптическая кривая • Функции Якоби • Интеграл • Функции Другие: Верзьера Аньези • Декартов лист • Кубика • Полукубическая парабола • Строфоида • Циссоида Диокла
Лемнискаты	Бернулли (Овал Кассини) • Бута • Жероно
Аппроксимационные	Сплайн (B-сплайн • Кубический • Моносплайн • Эрмита) • Безье
Циклоидальные	Кардиоида • Нефроида • Дельтоида • Астроида • Улитка Паскаля
Плоские трансцендентные
Спирали	Архимедова (Ферма) • Гиперболическая • «Жезл» • Клотоида • Логарифмическая
Циклоидальные	Циклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды)
Другие	Квадратриса • Погони (Трактриса) • Трохоида • Цепная линия (перевёрнутая арочная) • Постоянной ширины • Синусоида
Фрактальные
Простые	Коха • Леви • Минковского • Пеано
Топологические	Салфетка + Ковёр Серпинского • Губка Менгера