Кривая Безье | это... Что такое Кривая Безье? (original) (raw)

Кривы́е Безье́ или Кривы́е Бернште́йна-Безье́ были разработаны в 60-х годах XX века независимо друг от друга Пьером Безье (Pierre Bézier) из автомобилестроительной компании «Рено» и Полем де Кастельжо (Paul de Faget de Casteljau) из компании «Ситроен», где применялись для проектирования кузовов автомобилей.

Несмотря на то, что открытие де Кастельжо было сделано несколько ранее Безье (1959), его исследования не публиковались и скрывались компанией как производственная тайна до конца 1960-х.

Кривая Безье является частным случаем многочленов Бернштейна, описанных Сергеем Натановичем Бернштейном в 1912 году.

Впервые кривые были представлены широкой публике в 1962 году французским инженером Пьером Безье, который, разработав их независимо от де Кастельжо, использовал их для компьютерного проектирования автомобильных кузовов. Кривые были названы именем Безье, а именем де Кастельжо назван разработанный им рекурсивный способ определения кривых (алгоритм де Кастельжо).

Впоследствии это открытие стало одним из важнейших инструментов систем автоматизированного проектирования и программ компьютерной графики.

Содержание

1 Определение
2 Виды кривых Безье
3 Построение кривых Безье
4 Применение в компьютерной графике
5 Преобразование квадратичных кривых Безье в кубические
6 Ссылки
7 Литература
8 См. также
9 Примечания

Определение

Кривая Безье — параметрическая кривая, задаваемая выражением

$\mathbf{B}(t)=\sum^n_{i=0} \mathbf{P}_i \mathbf{b}_{i,n}(t),\quad 0\leqslant t\leqslant 1$

где $\mathbf{P}_i$ — функция компонент векторов опорных вершин, а $\mathbf{b}_{i,n}(t)$ — базисные функции кривой Безье, называемые также полиномами Бернштейна.

$\mathbf{b}_{i,n}(t)={n \choose i} t^i(1-t)^{n-i}$ ,

где ${n \choose i}=\frac{n!}{i!(n-i)!}$ — число сочетаний из по , где — степень полинома, — порядковый номер опорной вершины.

Виды кривых Безье

Линейные кривые

При n = 1 кривая представляет собой отрезок прямой линии, опорные точки P0 и P1 определяют его начало и конец. Кривая задаётся уравнением:

$\mathbf{B}(t)=(1-t)\mathbf{P}_0 + t\mathbf{P}_1 \quad t \in [0,1]$ .

Квадратичные кривые

Квадратичная кривая Безье (n = 2) задаётся 3-мя опорными точками: P0, P1 и P2.

$\mathbf{B}(t) = (1 - t)^{2}\mathbf{P}_0 + 2t(1 - t)\mathbf{P}_1 + t^{2}\mathbf{P}_2, \quad t \in [0,1]$ .

Квадратичные кривые Безье в составе сплайнов используются для описания формы символов в шрифтах TrueType и в SWF файлах (в SWF также могут использоваться кубические кривые Безье).

$t = \frac{\mathbf{P}_0 - \mathbf{P}_1 \pm \sqrt{(\mathbf{P}_0 - 2\mathbf{P}_1 + \mathbf{P}_2)\mathbf{B} + \mathbf{P}_1^2 - \mathbf{P}_0\mathbf{P}_2}}{\mathbf{P}_0 - 2\mathbf{P}_1 + \mathbf{P}_2}, \quad \mathbf{P}_0 - 2\mathbf{P}_1 + \mathbf{P}_2 \neq 0$

$t = \frac{\mathbf{B} - \mathbf{P}_0}{2(\mathbf{P}_1 - \mathbf{P}_0)}, \quad \mathbf{P}_0 - 2\mathbf{P}_1 + \mathbf{P}_2 = 0, \quad \mathbf{P}_0 \neq \mathbf{P}_1$

$t = \sqrt{\frac{\mathbf{B} - \mathbf{P}_0}{\mathbf{P}_2 - \mathbf{P}_1}}, \quad \mathbf{P}_0 = \mathbf{P}_1 \neq \mathbf{P}_2$

Кубические кривые

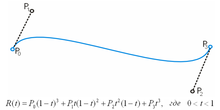
В параметрической форме кубическая кривая Безье (n = 3) описывается следующим уравнением:

$\mathbf{B}(t) = (1-t)^3\mathbf{P}_0 + 3t(1-t)^2\mathbf{P}_1 + 3t^2(1-t)\mathbf{P}_2 + t^3\mathbf{P}_3, \quad t \in [0,1]$ .

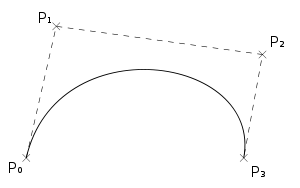
Кубическая кривая Безье

Четыре опорные точки P0, P1, P2 и P3, заданные в 2-х или 3-мерном пространстве определяют форму кривой.

Линия берёт начало из точки P0 направляясь к P1 и заканчивается в точке P3 подходя к ней со стороны P2. То есть кривая не проходит через точки P1 и P2, они используются для указания её направления. Длина отрезка между P0 и P1 определяет, как скоро кривая повернёт к P3.

В матричной форме кубическая кривая Безье записывается следующим образом:

$\mathbf{B}(t) = \begin{bmatrix}t^3&t^2& t& 1\end{bmatrix}\mathbf{M}_B \begin{bmatrix}\mathbf{P}_0\\\mathbf{P}_1\\\mathbf{P}_2\\\mathbf{P}_3\end{bmatrix}$ ,

где $\mathbf{M}_B$ называется базисной матрицей Безье:

$\mathbf{M}_B = \begin{bmatrix}-1&3&-3&1\\3&-6&3&0\\-3&3&0&0\\1&0&0&0\end{bmatrix}$

В современных графических системах и форматах, таких как PostScript (а также основанные на нём форматы Adobe Illustrator и Portable Document Format (PDF)), Scalable Vector Graphics (SVG), Metafont, CorelDraw и GIMP для представления криволинейных форм используются сплайны Безье, составленные из кубических кривых. SVG также позволяет работать со сплайнами Безье 4-й степени[1].

Построение кривых Безье

Линейные кривые

Параметр t в функции, описывающей линейный случай кривой Безье, определяет где именно на расстоянии от P0 до P1 находится B(t). Например, при t = 0,25 значение функции B(t) соответствует четверти расстояния между точками P0 и P1. Параметр t изменяется от 0 до 1, а B(t) описывает отрезок прямой между точками P0 и P1.

Bezier linear anim.gif

Квадратичные кривые

Для построения квадратичных кривых Безье требуется выделение двух промежуточных точек Q0 и Q1 из условия чтобы параметр t изменялся от 0 до 1:

Точка Q0 изменяется от P0 до P1 и описывает линейную кривую Безье.
Точка Q1 изменяется от P1 до P2 и также описывает линейную кривую Безье.
Точка B изменяется от Q0 до Q1 и описывает квадратичную кривую Безье.

Построение квадратичной кривой Безье	Анимация t: [0; 1]

Кривые высших степеней

Для построения кривых высших порядков соответственно требуется и больше промежуточных точек. Для кубической кривой это промежуточные точки Q0, Q1 и Q2, описывающие линейные кривые, а также точки R0 и R1, которые описывают квадратичные кривые: более простое уравнение p0q0/p0q1=q1p1/p1p2=bq0/q1q0

Построение кубической кривой Безье	Анимация t: [0; 1]

Для кривых четвёртой степени это будут точки Q0, Q1, Q2 и Q3, описывающие линейные кривые, R0, R1 и R2, которые описывают квадратичные кривые, а также точки S0 и S1, описывающие кубические кривые Безье:

Построение кривой Безье 4-й степени	Анимация t: [0; 1]

Свойства кривой Безье

непрерывность заполнения сегмента между начальной и конечной точками;
кривая всегда располагается внутри фигуры, образованной линиями, соединяющими контрольные точки;
при наличии только двух контрольных точек сегмент представляет собой прямую линию;
прямая линия образуется при коллинеарном (на одной прямой) размещении управляющих точек;
кривая Безье симметрична, то есть обмен местами между начальной и конечной точками (изменение направления траектории) не влияет на форму кривой;
масштабирование и изменение пропорций кривой Безье не нарушает ее стабильности, так как она с математической точки зрения «аффинно инвариантна»;
изменение координат хотя бы одной из точек ведет к изменению формы всей кривой Безье;
степень кривой всегда на одну ступень ниже числа контрольных точек. Например, при трех контрольных точках форма кривой — парабола;
окружность не может быть описана параметрическим уравнением кривой Безье;
невозможно создать параллельные кривые Безье, за исключением тривиальных случаев (прямые линии и совпадающие кривые).

Применение в компьютерной графике

Благодаря простоте задания и манипуляции, кривые Безье нашли широкое применение в компьютерной графике для моделирования гладких линий. Кривая целиком лежит в выпуклой оболочке своих опорных точек. Это свойство кривых Безье с одной стороны значительно облегчает задачу нахождения точек пересечения кривых (если не пересекаются выпуклые оболочки опорных точек, то не пересекаются и сами кривые), а с другой стороны позволяет осуществлять интуитивно понятное управление параметрами кривой в графическом интерфейсе с помощью её опорных точек. Кроме того аффинные преобразования кривой (перенос, масштабирование, вращение и др.) также могут быть осуществлены путём применения соответствующих трансформаций к опорным точкам.

Наибольшее значение имеют кривые Безье второй и третьей степеней (квадратичные и кубические). Кривые высших степеней при обработке требуют большего объёма вычислений и для практических целей используются реже. Для построения сложных по форме линий отдельные кривые Безье могут быть последовательно соединены друг с другом в сплайн Безье. Для того, чтобы обеспечить гладкость линии в месте соединения двух кривых, три смежные опорные точки обеих кривых должны лежать на одной прямой. В программах векторной графики наподобие Adobe Illustrator или Inkscape подобные фрагменты известны под названием «путей» (path).

Преобразование квадратичных кривых Безье в кубические

Квадратичная кривая Безье с координатами $(x_0;y_0),\,(x_1;y_1),\,(x_2;y_2)$ преобразовывается в кубическую кривую Безье с координатами $(x_0;y_0),\,\left(x_0+\frac{2 \cdot (x_1-x_0)}{3}; y_0+\frac{2 \cdot (y_1-y_0)}{3}\right),\,\left(x_1+\frac{x_2-x_1}{3}; y_1+\frac{y_2-y_1}{3}\right),\,(x_2;y_2)$ .

Ссылки

Wolfram Math World Bézier Curve (англ.)
American Mathematical Society From Bézier to Bernstein (англ.)
Кривые Безье в компьютерных играх [1] (рус.)

Литература

Роджерс Д., Адамс Дж. Математические основы машинной графики. — М.: Мир, 2001.

См. также

	Category:Bezier Curves на Викискладе?

Примечания

↑ World Wide Web Consortium (W3C) Scalable Vector Graphics (SVG) 1.1 (Second Edition). Chapter 8: Paths (en-US) (16 августа 2011). — W3C Recommendation. Архивировано из первоисточника 24 июня 2012. Проверено 21 мая 2012.

Кривые
Определения	Аналитическая • Жордана • Канторова • Урысона • Овал • Спрямляемая Радиус кривизны
Преобразованные	Эволюта • Эвольвента • Подера • Антиподера • Параллельная • Дуальная • Каустика
Неплоские	Винтовая линия • Линия откоса • Локсодрома • Ортодромия • Губка
Плоские алгебраические
Конические сечения	Гипербола • Парабола • Эллипс (Окружность)
3-й порядок	Эллиптические: Эллиптическая кривая • Функции Якоби • Интеграл • Функции Другие: Верзьера Аньези • Декартов лист • Кубика • Полукубическая парабола • Строфоида • Циссоида Диокла
Лемнискаты	Бернулли (Овал Кассини) • Бута • Жероно
Аппроксимационные	Сплайн (B-сплайн • Кубический • Моносплайн • Эрмита) • Безье
Циклоидальные	Кардиоида • Нефроида • Дельтоида • Астроида • Улитка Паскаля
Плоские трансцендентные
Спирали	Архимедова (Ферма) • Гиперболическая • «Жезл» • Клотоида • Логарифмическая
Циклоидальные	Циклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды)
Другие	Квадратриса • Погони (Трактриса) • Трохоида • Цепная линия (перевёрнутая арочная) • Постоянной ширины • Синусоида
Фрактальные
Простые	Коха • Леви • Минковского • Пеано
Топологические	Салфетка + Ковёр Серпинского • Губка Менгера